Bonjour,
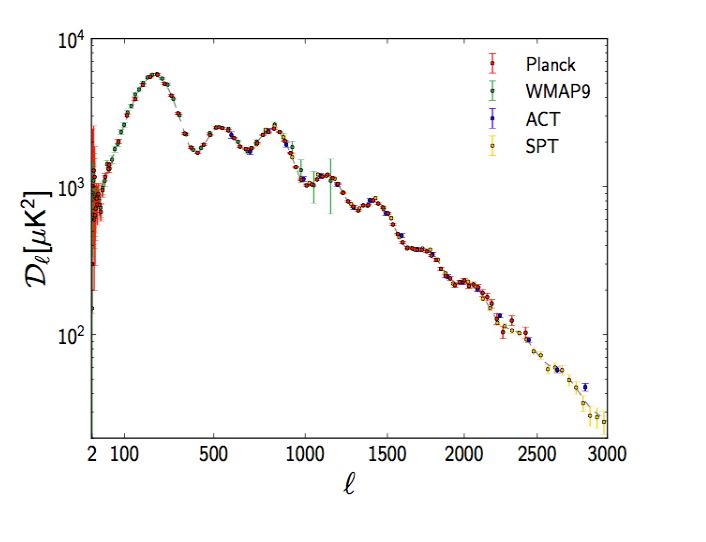
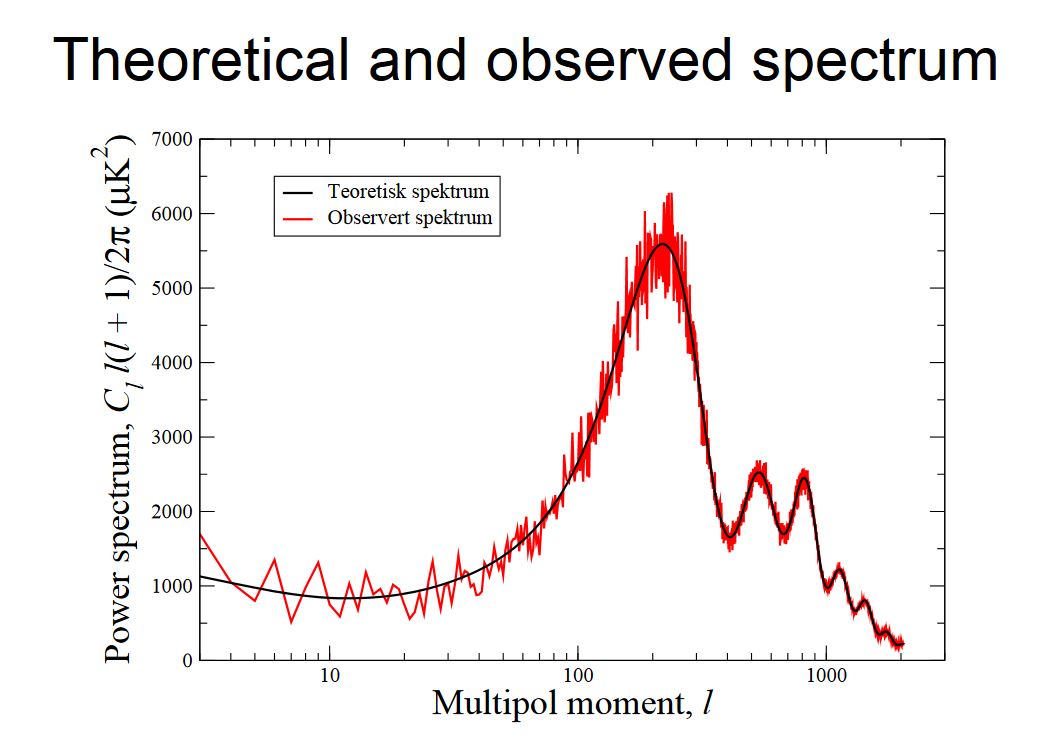
Dans ce graphique sur les anisotropies du CMB, l'auteur (un expert) nous dit :
La courbe représente la corrélation de température (en micro-Kelvin au carré µK2) en fonction de la taille regardé sur le ciel l.
Pourriez vous me dire en quoi (quelle unité se mesure l ?)
Je pensais que ce graphique était lié à des corrélations angulaires...
Merci
Pour en savoir plus => l'analyse de ces anisotropies par cet expert en analyse du CMB => ici
Voici un cours en slides qui détaille les harmoniques sphériques et leur utilisation dans l'étude du spectre de puissance du CMB que tu évoques ici. Il y a beaucoup de détail sur la cosmologie qu'on peut déduire de ces observations (par contre c'est en anglais) :
https://cmb.wintherscoming.no/pdfs/A...ctrum_2015.pdf
Merci.
L'anglais ne m' a pas causé de souci, par contre j'ai été dépassé par le niveau de l'explication mathématique.
Du coup je sais toujours pas à quoi correspond ce l, . dans le graphe que j'ai cité il parle de longueur et dans celui de l'article il l’appelle le "multipol moment "
Bonsoir,
Le multipole «*l*» est inversement proportionnel à la distance angulaire. La relation précise est.
Merci.
Avec la formule et le graphique je peux commencer à faire quelques calculs.
Si on prend la valeur de 1000 pour le moment du multipôle on obtient une distance angulaire = 2 PI/1000 donc en approximant Pi à trois on obtient : 6/1000 = 0,006 degré en radian
Cela veut t'il dire que c'est la température en fonction de l'angle d'observation que l'on mesure ?
Merci
Envoyé par pachacamac
Merci.
Avec la formule et le graphique je peux commencer à faire quelques calculs
Si on prend la valeur de 1000 pour le moment du multipôle on obtient une distance angulaire = 2 PI/1000 donc en approximant Pi à trois on obtient : 6/1000 = 0,006 degré en radian
Cela veut t'il dire que c'est la température en fonction de l'angle d'observation que l'on mesure ?
Merci
Le CMB est assimilable à un bruit de fond : on a ni plus ni moins que des ondes sonores qui se propagent dans le plasma originel. L'amplitude des ondes sonores se traduit par une différence locale de pression, qui elle même se traduit en variation de température, avec une amplitude sur le CMB de l'ordre d'une dizaines de µK.
La lettre l dénote la longueur d'onde prise sur la sphère unité et c'est beaucoup plus facile à visualiser avec une animation :
https://www.youtube.com/watch?v=Ziz7t1HHwBw
Maintenant que tu visualises ce qu'est une harmonique sphérique (l, m) on revient sur la sphère céleste du CMB. Comme il s'agit d'un bruit, tous ces modes (l,m) sont présents et se mélangent comme des clapotis agitant une surface d'eau libre, mais tous les modes n'ont pas la même amplitude moyenne. De la même façon que dans le spectre d'une source sonore la puissance émise dans les graves et les aigus varie selon la source, ce qui caractérise son timbre. Ainsi par exemple le bruit produit en toquant une paroi mince permet de la différencier d'un mur épais : le spectre sonore transporte beaucoup d'information sur la physique du phénomène. De la même façon le spectre des anisotropies du CMB est extrêmement riche en informations et contraint des paramètres aussi fondamentaux que la densité de matière baryonique et noire dans le plasma originel. Mesurer ce spectre consiste à quantifier la puissance émise, avec l (on oublie m) sur l'axe des abcisses et la puissance émise par mode sur l'axe des ordonnées.
edit: une simulation en ligne qui permet de visualiser le spectre attendu du CMB en fonction de la valeur des omega (matière baryonique, matière noire, énergie sombre)
https://plancksatellite.org.uk/cmb-sim/
Dernière modification par Gilgamesh ; 13/06/2024 à 17h38.
Parcours Etranges
Merci Gilgamesh.
Le petit film permet de visualiser les harmoniques sphériques mais il s'arrette à l=3 alors que dans les graphiques ci-dessus l va jusque 1000 ou 3000, c'est normal ? en tout cas pour visualiser c'est une autre paire de manche.
J'ai aussi regarder à harmonique sphérique sur wikipédia, c'est intéressant mais c'est du très lourd ( trop lourd pour moi ) en math.
A la fin de l'article, le l qu'ils utilisent semble correspondre au l , le nombre quantique célèbre en atomistique...
Encore une petite question : pour obtenir les graphiques ci-dessus à t'on deja utilisé une transformation de Fourrier ?
Sur les ondes acoustiques qui se propagent dans ce plasma ?
Merci
J'ai eu les réponses à mes questions sur cet ancien post de futura où interviennent entre autre Gilgamesh et physeb2.
A part les très grandes lignes j'en retiens surtout que l'analyse de cette courbe est trop compliquée pour moi:
physeb2 : " Il m'a fallut la moitié de mon doctorat pour comprendre ces trucs là "
Gilgamesh :"on calcule le laplacien (en coordonnée sphériques) ΔT. On pose que ΔT = 0 La résolution de cette équation de Laplace, qui implique divers outils mathématique comme les polynômes de Legendre, donne les harmoniques sphériques."
Je jette l’éponge vu mon niveau de math insuffisant.
Dernière modification par pachacamac ; 14/06/2024 à 09h05.
Finalement je reprend :
Pour commencer Je vais regarder du côté du laplacien
Je pose aussi ici cette page : https://fr.wikibooks.org/wiki/Cosmol...du_fond_diffus
Pour essayer de comprendre l’opérateur laplacien avec les mains.
On part d’un champ scalaire : un nombre réel en chaque point de l’espace, ici une température.
Formellement, si on “nourrit” l’opérateur gradient avec un champ scalaire, cela donne un champ de vecteurs. En raisonnant à une dimension, si j’ai une tige de métal que je chauffe à une extrémité, l’opérateur gradient me dira de combien la température varie par unité de longueur (le gradient est une dérivée spatiale). Plus le matériau est isolant, plus le gradient sera élevé, ce qui donne la longueur du vecteur grad et le sens de variation de la température donnera son orientation.
Dans un milieu où la température varie en chaque point, le sens du gradient va alterner entre les zones chaudes et froides.
Si j’isole une surface fermée et que je somme mentalement tous les vecteurs qui entrent et sortent, j’obtiens la divergence. La divergence est l’opération comptable sur les vecteurs d'entrées-sorties : on additionne les contributions et si c’est positif, la densité de ce que je mesure augmente avec le temps dans le périmètre mesuré, tandis que si c’est négatif, le périmètre se vide.
Formellement, la divergence opère à l’inverse de l’opérateur gradient : on lui donne un champ de vecteurs et cela donne un scalaire.
Ici, le “fluide” est un gradient. Intuitivement, on comprend que si on somme tous les écarts de température sur une surface (ici le fond du ciel), cela donne zéro, de la même façon que si je somme tous les creux et les bosses à la surface de la mer, j’obtiens zéro.
D’où :
div(gradT)=0
Dernière modification par Gilgamesh ; 16/06/2024 à 15h55.
Parcours Etranges
Merci Gilgamesh de tenter de me faire comprendre un peu plus ces notions.
Avant de répondre à ton dernier post, voici ce que j'ai compris sur l'analyse du spectre de puissance du CMB à partir de tes explications et de celles de physeb2 dans l’excellent fils cité en #9
Avant tout j'ai compris que pour comprendre cette analyse il faut impérativement un niveau en math/physique que je n'ai pas.
Je peux admette par exemple, comme le dit physeb2, que le laplacien s'annule pour les fonctions harmoniques , ou que l'on décompose la carte des températures du CMB en harmoniques sphériques, mais de là à vraiment comprendre le pourquoi et le comment il y a un monde accessible uniquement à ceux qui ont fait des études poussées en ce domaine et qui connaissent en prérequis les fonctions de Legendre..
En plus physeb2 nous dit que c'est encore plus compliqué et qu'il faut faire entre autre appel à l’équation de Boltzmann (la seule que je connaisse de lui est S= klogw) avec d'autre subtilités.
Donc je crois avoir appris et compris ce que représente ce graphique : c'est la variance à toute les échelles de la distribution des températures sur la sphère du CMB. Et si je vois maintenant un peu les méthodes utilisées pour l'obtenir, les détails calculatoires me dépassent et me dépasseront pour toujours.
Maintenant pour les opérateurs différentiels : le laplacien, le gradient et la divergence.
Merci pour tes explications très simples mais il y a quelque chose qui me gène...
Prenons l’opérateur le plus simple pour moi le gradient.
Je comprend bien le gradient de température d'une tige que l'on chauffe à une extrémité ou le gradient d'un champs continu comme celui de la pesanteur terrestre. Mais quand la valeur de la température change de point en point de manière presque aléatoire comme tu dis: "Dans un milieu où la température varie en chaque point, le sens du gradient va alterner entre les zones chaudes et froides."
je dirai aussi qu'en plus du sens sa valeur change aussi.
Donc on va obtenir "une carte" du champs de vecteur par exemple des températures terrestres ou de celle du CMB avec des vecteurs dans tous les sens de longueurs différentes et là j'ai du mal à voir comment on peut utiliser cela concrètement et/ou dans les équations... je vois pas du tout comment on peut exprimer gradT... (même si on peut l'utiliser sans rien préciser dans des expressions analytiques)
Ensuite on peut avec la divergence obtenir le laplacien et comme tu l'expliques : div(gradT)=0
Okay, mais j'ai l'impression que si on mettait au hasard n'importe quelles valeurs de température pour chaque points du CMB cette relation serait encore valable..donc finalement à quoi ça sert de faire les mesures ?
J' espère que j'ai exprimé de manière compréhensible mes incompréhensions
Merci encore
Dernière modification par pachacamac ; 16/06/2024 à 17h08.
En fait j'ai un peu de difficulté à relier le coté expérimental ( les mesures de température du CMB) et la théorie avec le laplacien et les coordonnées sphériques.
Pourrais tu me lister chronologiquement les premières opérations que l'on fait subir à ses mesures pour obtenir le spectre de puissance du CMB et a quel moment on obtient les harmoniques sphériques
Tu avais écrit dans l'autre post :
On part d'un fichier de points de mesure : pour chaque point sur la sphère céleste (~107 pour le CMB), on dispose d'une valeur de la température, ça définit un champ scalaire T.
A partir de ça on calcule le laplacien (en coordonnée sphériques) ΔT.
Soit mais à partir de quoi ?
Je pensais avoir compris que le laplacien est = 0 vu que la divergence du gradient du champs de température est nulle.
Donc à part ça on utilise quoi pour faire ce calcul ?
On pose que ΔT = 0
La résolution de cette équation de Laplace, qui implique divers outils mathématique comme les polynôme de Legendre, donne les harmoniques sphériques.
Aussi je pense me rappeler que ce spectre de puissance avait été obtenue de manière théorique avant les mesures faites sur le CMB . C'est exact ?
Merci
Le laplacien c'est juste pour introduire les harmoniques sphériques : par définition en mathématiques, les harmoniques sphériques sont des fonctions harmoniques dont le laplacien est nul. La démonstration de ce résultat est techniquement un peu costaude mais ça se trouve sur wiki :
https://fr.wikipedia.org/wiki/Harmonique_sph%C3%A9rique
Bon, mais nous on est des physiciens
Intuitivement je comprends ça facilement par le fait que sur la surface les bosses et les creux s'annulent, cela me suffit pour m'en faire une idée correcte et je laisse la technicité de la démonstration aux mathématiciens. Je te suggère d'en faire autant.
Nous ce qui nous intéresse sur le CMB c'est que cette fonction donnant les harmoniques sphériques existe et s'exprime proprement par cette magnifique fonction que chaque peut implémenter sur le logiciel de son choix :
Yℓ,m(θ,φ) = √[((2ℓ + 1)/4π)((ℓ − m)!/(ℓ + m)!] Pℓ,m(cosθ)eimφ
avec
ℓ le multipole 0, 1, 2, ... 1000 etc
m allant de −ℓ à +ℓ
θ la lattitude (−π à +π)
φ la longitude (0 à 2π)
Pℓ,m le polynôme de Legendre.
Ça nous donne ces belles fonctions régulières sur la sphère vu dans la vidéo. Voilà, le boulot des maths pures est terminé, maintenant c'est de la Physique. Car le fond de température évidemment n'est pas une belle fonction régulière mais un bruit.
En chaque point on définit notre champs scalaire des température sous forme d'une différence de la température locale T(θ,φ) avec la moyenne <T>
δT(θ,φ) = (T(θ,φ) - <T>)/<T>
Et maintenant on dit que cet écart de température en chaque point sur la sphère δT(θ,φ) est égal à la somme sur tous les ℓ,m (noté Σℓ,m ci-dessous) des harmoniques sphériques Yℓ,m(θ,φ) multipliées par un coefficient aℓ,m
δT(θ,φ) = Σℓ,m aℓ,m Yℓ,m(θ,φ)
Les coefficient aℓ,m sont les inconnus qu'on veut déduire : on mesure δT, on calcule Yℓ,m => on en déduit aℓ,m.
Le spectre de puissance est proportionnel à la variance de ces aℓ,m
Cℓ ~ Var(aℓ,m)
et la quantité représentée sur le graphique pour chaque multipole ℓ c'est ℓ(ℓ + 1)Cℓ
Dernière modification par Gilgamesh ; 16/06/2024 à 20h18.
Parcours Etranges
Merci beaucoup ! C'est très clair.
Maintenant j'ai tout compris ( sauf les démonstrations mathématiques )
Dernière modification par pachacamac ; 16/06/2024 à 22h07.
Bonjour,
En continuant sur la piste des anisotropies du CMB , de fils en aiguille je suis arrivé sur l'article original de Mukhanov et Chibisov
Quantum fluctuations and a nonsingular Universe
V.F.Mukhanov and G.V. Chibisov -1981
Je me rappelle aussi que Mukhanov avait prédit la valeur de l'indice spectral du CMB: n_s = 0,96 vérifiée par WMAP et Planck avec une grande précision.
Par contre j'ai pas pu trouver une explication simple de ce qu 'était l' indice spectral du CMB
Toute aide bienvenue.
Aussi dans son livre, 442 pages en anglais , accessible gratuitement en ligne : Physical Foundations of Cosmology
Au chapitre 9 il traite très en profondeur les "Cosmic microwave background anisotropies "
Attention c'est du lourd au niveau équations
Merci
