Bonjour,
Le big bang a eu lieu il y a environ 13 milliards d'années. Si tout ce qui en est sorti s'était déplacé à la vitesse de la lumière (ce qui est impossible), alors le diamètre de l'univers devrait être actuellement de 26 milliards d'années. Pas 93.
D'où provient cete contradiction?
Un civet, un plat de côtes et puis, glissez-moi une petite paupiette avec.( Lino Ventura)
Avez vous lu le Wiki que vous avez mis en image? c'est expliqué, qu'est-ce qui vous pose problème?
Le wiki dit:
C'est une autre question de savoir à quelle distance géométrique se situent actuellement les objets dont nous recevons la lumière, 13,8 milliards d'années après qu'ils l'ont émise. Pour déterminer cette distance, il faut adopter un modèle d'univers et connaissant la vitesse d'expansion de l'espace en déduire la distance dont se sera éloigné l'objet considéré depuis l'émission des photons. Dans le cadre du modèle standard de la cosmologie, la distance actuelle de l'horizon cosmologique est de l'ordre de 46,5 milliards d'années-lumière. Le diamètre de l'Univers observable est estimé à environ 93 milliards d'années-lumière
Considérons un objet dont nous recevons la lumière maintenant, émise il y a 13,8 milliards d'années.
Cet objet se trouve actuellement non plus à 13,8 milliards d'années-lumière, mais - compte tenu de la vitesse d'expansion de l'espace - à 46,5 milliards d'années-lumière.
Il a donc parcouru 46,5 - 13,8 = 32,7 milliards d'années-lumière en seulement 13,8 milliards d'années.
Cela signifierait donc que la vitesse d'expansion de l'espace est largement supérieure à la vitesse de la lumière.
Cela n'est-il pas en contradiction avec la théorie de la relativité?
Je crois en effet me rappeler que si un objet approche de la vitesse de la lumière, il voit sa masse augmenter. Elle devient même très importante (infinie?) lorsque ka vitesse de la lumière est atteinte. Mais dans notre cas, elle est non seulement atteinte, mais largement dépassée.
Un civet, un plat de côtes et puis, glissez-moi une petite paupiette avec.( Lino Ventura)
[QUOTE=Yvan_Delaserge;7227379]
Non car l'expansion n'a pas de vitesse mais un taux:https://fr.wikipedia.org/wiki/Expansion_de_l%27UniversCela n'est-il pas en contradiction avec la théorie de la relativité?
Non, la masse (au sens moderne) est un invariant :https://www.universalis.fr/encyclope...e-relativiste/Je crois en effet me rappeler que si un objet approche de la vitesse de la lumière, il voit sa masse augmenter. Elle devient même très importante (infinie?) lorsque ka vitesse de la lumière est atteinte. Mais dans notre cas, elle est non seulement atteinte, mais largement dépassée.
Désolé de renvoyer vers des liens, mais trop peu de temps pour faire plus...
Le premier lien stipule, entre autres, que:
Si elle était généralisée à grande échelle, l'interprétation Doppler pourrait soulever un paradoxe, car elle signifierait que des objets suffisamment lointains s'éloigneraient à des vitesses supérieures à celle de la lumière et, de ce fait, enfreindraient les lois de la relativité restreinte. Il n'en est rien dans les faits, car si ces objets se déplacent bien avec une vitesse relative plus grande que celle de la lumière, cela ne permet pas d'échange d'information à de telles vitesses. Ainsi l'accroissement de la distance mutuelle entre galaxies, dû à l'expansion de l'espace, n'est pas en conflit avec la relativité restreinte.
Je peine à comprendre la signification de
" si ces objets se déplacent bien avec une vitesse relative plus grande que celle de la lumière, cela ne permet pas d'échange d'information à de telles vitesses".
Qui échange de l'information avec qui? Admettons que l'échange d'information soit constitué de la lumière que nous recevons d'une étoile. La phrase devient:
" si l'étoile se déplace bien avec une vitesse relative plus grande que celle de la lumière, cela ne permet pas de voir la lumière de l'étoile à de telles vitesses".
Donc, on voit l'étoile, mais on ne la voit pas parce qu'elle se déplace plus vite que la lumière?
Le second lien dit en résumé que:
Les principes de la relativité restreinte développée par Albert Einstein ont bousculé le concept classique de masse. L'équivalence proclamée entre la masse M et l'énergie E d'un corps au repos permet de mesurer les masses par leur équivalent en énergie et abolit la loi d'additivité des masses. La masse relativiste reste cependant une propriété intrinsèque fondamentale des particules, grâce en particulier au fait que sa valeur est indépendante de la vitesse du référentiel dans lequel on la mesure ; la masse constitue en ce sens un invariant de Lorentz, insensible aux phénomènes relativistes de contraction ou de dilatation.
Donc d'un côté selon la relativité restreinte, la masse varie selon la vitesse, mais d'un autre côté elle est indépendante de la vitesse.
Certaines notions sont certes irréfutables mathématiquement, je n'en disconviens en aucun cas, mais difficiles à comprendre intuitivement.
Un civet, un plat de côtes et puis, glissez-moi une petite paupiette avec.( Lino Ventura)
Premier point :
La limitation par la vitesse de la lumière est locale. C'est à dire que pour astre dont la distance à la Terre augmente de plus de 300 000 km à chaque seconde, il ne se passe rien de particulier : il peut se considérer comme immobile et considérer que la lumière va à 300 000 km/s dans toutes les directions par rapport à lui.
Si on note r les distances à la Terre et t le temps cosmologique, alors en fonction de la distance r un astre comobile aura une vitesse coordonnée v=dr/dt et la lumière au voisinage de cet astre aura pour vitesse coordonnée v+c si elle part à l'opposé de la Terre et v-c si elle part en direction de la Terre. La vitesse coordonnée n'est pas bornée par la valeur c, par contre les valeurs de vitesse coordonnée de la lumière bornent les autres vitesses coordonnées. En ce sens, même si on peut avoir des vitesses coordonnées plus grande que 300 000 km/s, elles restent inférieures aux vitesse coordonnées de la lumière.
Si à la distance r on a v>c, alors la lumière émise vers la Terre avance en quelque sorte à reculons, elle est entrainée par l'expansion (notons que ça ne l'empêche pas forcement de finir par atteindre la Terre, mais on ne va pas compliquer pour l'instant).
Deuxième point :
La vulgarisation est truffée du concept désuet de masse relativiste qui génère beaucoup de confusion (l'usage de "masse relativiste" est par ailleurs fautif dans le passage cité...)
-La masse est un invariant (elle ne dépend pas de la vitesse) mais ne se conserve pas (deux photons de masse nulle peuvent générer, en faisant collision, une paire particule/antiparticule de masse non nulle, ou inversement). Autrefois on l'appelait "masse au repos", aujourd'hui on parle simplement de "masse"
-L'énergie (ainsi que la quantité de mouvement) n'est pas invariante (elle dépend de la vitesse) mais se conserve (les deux photons et la paire particule/antiparticule résultantes ont la même énergie). L'énergie intègre une composante cinétique (qui vaut mv²/2 pour des faibles vitesses) et une composante due à la masse (le fameux mc²). Cette énergie divisée par c² donne la fameuse "masse relativiste" qui varie avec la vitesse. Cette "masse relativiste" n'est plus utilisée aujourd'hui.
m@ch3
Never feed the troll after midnight!
Exact, mea culpa, pour lire le reste du lien il faut être abonné...pas fais gaffe.Envoyé par mach3
Serait-il correct de dire que:
L'expansion de l'univers peut sembler plus rapide que la vitesse de la lumière en raison de la manière dont nous mesurons les vitesses dans le contexte de la cosmologie. Lorsque l'univers s'expand, il n'y a pas de restriction à la vitesse à laquelle l'espace lui-même peut se dilater. Cela signifie que deux points de l'univers peuvent s'éloigner l'un de l'autre à une vitesse supérieure à la vitesse de la lumière.
Cependant, il est important de noter que cette notion ne viole pas la relativité restreinte d'Einstein, car la relativité restreinte s'applique aux objets se déplaçant à travers l'espace, tandis que l'expansion de l'univers concerne la façon dont l'espace lui-même se dilate. Les objets distants ne sont pas en train de se déplacer à des vitesses supérieures à celle de la lumière par rapport à nous, mais ils sont emportés par l'expansion de l'espace entre eux et nous.
Un civet, un plat de côtes et puis, glissez-moi une petite paupiette avec.( Lino Ventura)
Il me semble que selon la relativité restreinte, si un objet s'approche de la vitesse de la lumière, sa masse augmente, voire devient infinie si la vitesse de la lumière est atteinte. Donc la masse dépendrait bien de la vitesse?
Est-ce ma mémoire qui me trahit? C'est vrai que ça remonte à loin.
Un civet, un plat de côtes et puis, glissez-moi une petite paupiette avec.( Lino Ventura)
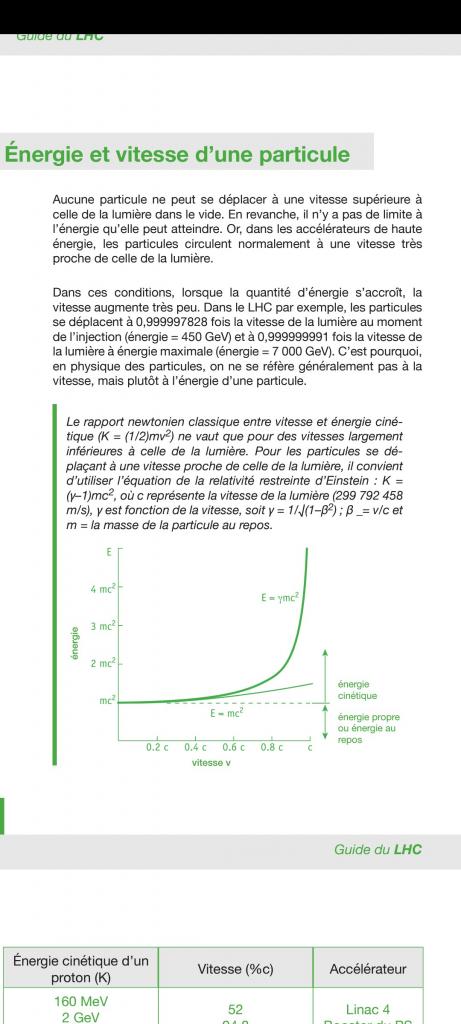Sur ce document du CERN, ils disent qu'en accélérant jusqu'au voisinage de la vitesse de la lumière, la vitesse des protons augmente très peu, mais par contre, leur énergie augmente. Ils se gardent bien de dire que leur masse augmente.
Un civet, un plat de côtes et puis, glissez-moi une petite paupiette avec.( Lino Ventura)
Bonsoir,
L'expansion de l'univers ne s'exprime pas en terme de vitesse car ça n'a pas de sens. Pour un âge cosmique donné, correspond un taux d'expansion, H, qui s'exprime en km/s/Mpc (kilomètre par seconde et par mégaparsec. Le mégaparsec représente 3,2616 méga années-lumière). Ce taux est la constante ou plutôt le paramètre de Hubble qui varie avec le temps. Il tend vers l'infini en remontant vers le bigbang. Actuellement il est proche de Ho =70 km/s/Mpc.
Si on ne considère que le phénomène d'expansion entre deux galaxies (on oublie la gravité), cela signifie qu'elles vont s'éloigner l'une de l'autre avec une vitesse de récession de 70 km/s si elles sont distantes d' 1 Mpc. Si la distance qui les sépare est de 100 Mpc, la vitesse de récession sera de 100 x 70 = 7000 km/s.
Bien sûr. "Actuellement" toute galaxie située à une distance supérieure à c/Ho = 300 000 / 70 ~ 4300 Mpc ~14 milliards d'années lumière nous fuit avec une vitesse supérieure à c.Cela signifie que deux points de l'univers peuvent s'éloigner l'un de l'autre à une vitesse supérieure à la vitesse de la lumière.
Celles qui se trouvent à la limite de l'univers observable ont une vitesse de récession de l'ordre de 3,2c.
Et retour des tachyon...
Moi ignare et moi pas comprendre langage avec «hasard», «réalité» et «existe».
Non, parce qu'à la limite de l'univers observable, la lumière émise vers nous s'éloigne à 2,2c et la lumière émise à l'opposée s'éloigne à 4,2c (tout ça en vitesse coordonnée bien-sûr). Les particules massives situées à la limite de l'univers observable s'éloignent à une vitesse comprise entre 2,2 et 4,2c. D'hypothétiques tachyons devraient s'éloigner à plus de 4,2c ou à moins de 2,2c (ce qui inclut se rapprocher).
Attention aussi à la section où nous nous trouvons. Soit on sait répondre aux questions du primo-posteur et on le fait, soit on ne sait pas et on se tait, mais on ne commente pas (en cas désaccord, ça doit se passer ailleurs).
m@ch3
Never feed the troll after midnight!
Un point est qu'une vitesse est une variation de distance par rapport au temps, mais que les mesures de distances à des échelles cosmologique étant problématiques, les mesures de vitesse aussi. Il y a plusieurs manières de mesurer une distance (règle, radar, parallaxe, luminosité,...) et dans la vie de tous les jours (vitesse lente, champ de gravité faible) toutes ces manières donnent le même résultat alors qu'en général ce n'est pas le cas (certaines devenant carrément impraticables aux échelles cosmologiques comme les mesures à la règle ou au radar).
Un autre point est que la vitesse d'un corps relativement à un autre est liée à l'angle hyperbolique entre les lignes d'univers de ces corps. En relativité restreinte, l'espace-temps étant plat, on à le droit aux translations et on peut donc évaluer cet angle de façon univoque peu importe les lignes d'univers considérée : on amène l'une jusqu'à l'autre par translation et on mesure l'angle. En relativité générale, l'espace-temps peut être courbe et on n'a plus le droit de faire des translations, seulement des transports parallèles qui généralisent la translation mais dont le résultat dépend du chemin suivi contrairement aux translations : selon comment on amène une ligne d'univers jusqu'à l'autre pour mesurer l'angle, on obtient un angle différent et seule une mesure de vitesse locale (les lignes d'univers se croisent ou presque) possède un sens univoque.
m@ch3
Never feed the troll after midnight!
Il faut bien distinguer deux types de mouvements. Pour ce faire, couvres mentalement l'univers d'un repère de coordonnés, c'est à dire d'un grand calque millimétré en trois dimensions. Sur ce calque tu places les objets et tu notes leur coordonnées r(x, y, z).
Une fois que tu as fais ça, tu peux concevoir les deux types mouvements :
- le mouvement propre : les coordonnées de l'objet changent avec le temps. Le mouvement propre explique la formation des galaxies et des amas : les objets attirent les objets proches et se regroupent pour former des masses liées. La vitesse propre de ce mouvement est inférieure ou égale à c. Strictement inférieure à c pour un corps de masse non nulle, strictement égale à c pour une particule de masse nulle.
- le mouvement comobile : les coordonnées de l'objet restent identiques, mais l’intervalle entre deux graduations grandit. Autrement dit, le calque est en expansion. Chaque objet voit tous les objets lointains s'éloigner de lui. La vitesse de récession entre deux objets n'est limitée par rien. Et s'il est possible de parler de vitesse de récession, comme précisé par Lansberg la notion de vitesse de l'expansion est vide de sens. Ce qui caractérise l'expansion à l'échelle de l'Univers à un âge cosmique donné c'est un taux d'expansion H, ratio de la vitesse de récession entre deux points sur la distance séparant ces deux points.
Dans ce qui suit, on va négliger totalement le mouvement propre pour ne raisonner que sur le mouvement comobile (et dans un univers euclidien c-à-d sans courbure, ce que l'univers réel semble être avec un bon degré d'approximation).
Dans la vie courante, la notion de distance est univoque, en cosmologie elle recouvre quatre notions bien distinctes.
La première notion de distance est en fait un temps : le temps de trajet du photon (ou temps de regard en arrière). C'est celle qui est donnée usuellement, en années-lumière. Ici les 13,5 milliards d'années-lumière que tu donnes pour la distance qui nous sépare du point A. Il s'agit bien d'années qu'a passé le photon dans l'espace, pour nous parvenir. Mais à quelle distance en mètre cela correspond ?
Dans un univers en expansion, il faut distinguer deux choses :
2- la distance entre nous et le point A au moment de l'émission du rayonnement que nous recevons aujourd'hui, c'est la distance dite angulaire Da
3- la distance entre nous et le point A au moment de la réception du photon, c'est à dire aujourd'hui, c'est la distance propre (ou comobile, r_comov dans l'abaque ci-dessous) Dp.
La distance angulaire Da est ainsi nommé parce que c'est celle qu'il faut prendre en compte pour juger de la taille angulaire de l'objet source sur la voute céleste. L'angle alpha (sous lequel on observe l'objet de taille h est :
alpha = h/Da
(pour les petits angles)
L'abaque ci-dessous te donne dans la colonne size 1" a combien de kpc (1 kpc = mille parsecs soit ~ 3300 années-lumière) correspond 1 seconde d'arc (1°/3600) et la colonne suivante l'angle en seconde sous lequel on voit un objet de 1 kpc en fonction de sa distance.
Donc, quand le photon a été émis, la source était la la distance Da de l'endroit où nous sommes. Et à ce moment là, le taux d'expansion H(t) était plus élevé que maintenant. Le photon "remonte" donc un "flot d'espace" comme un saumon remonte la rivière (à une vitesse propre constante : c) pour arriver jusqu'à nous.
Donc notre photon-saumon progresse, c'est à dire que à tous les instants la distance entre lui et la source diminue. Mais bien sur elle diminue bien plus lentement que ct puisque à chaque instant la distance augmente de Hd entre le photon situé à la distance d et l'observateur futur. Quand d et H était maximal (donc à l'émission) la progression était minimal. Puis peu à peu le photon-saumon progresse de plus en plus efficacement vers l'observateur, car la distance d diminue (c'est la principale raison) ainsi que le taux d'expansion.
En même temps qu'il progresse difficilement vers le futur observateur, la distance qui le sépare de sa source augmente plus vite que ct. Car en plus de la distance parcourue par les moyens propres du photons (soit ct) il faut ajouter la distance que rajoute l'expansion. Quand le photon-saumon regarde dans son rétroviseur, il voit une source qui s'éloigne de plus en plus vite de lui, quoique sa vitesse propre soit constante.
Quand il arrive à l'observateur et achève sa glorieuse (quoique monotone) existence sur la rétine de l'observateur, il a parcouru par ses moyens propres ct = 13,5 Gal mais la source est bien plus éloignée que cela désormais. Et cette distance réelle est ce qu'on appelle la distance propre. C'est la distance à laquelle se trouve aujourd'hui la source, après 13,5 Ga d'expansion.
Le ratio entre Da la distance angulaire (à l'émission) et Dp la distance propre (à la fin du trajet) est simple à calculer, il est égal par définition au ratio des facteurs d'échelle réception / émission, a0/a = 1 + z, a0 étant n'importe quelle distance mesurée aujourd'hui et a la même distance au moment de l'émission, z étant le décalage vers le rouge.
Dp = Da (1+z)
Reste une quatrième notion de distance à aborder, la distance de luminosité. Les objets lointains nous apparaissent comme étant très proches (Da relativement petit) mais par contre il sont beaucoup moins lumineux que ce que leur taille angulaire pourrait laisser supposer, car le photon-saumon en luttant contre le flot d'espace qui défilait sous lui, a perdu du 'gras', c'est à dire de l'énergie. Il arrive exténué à l'observateur : c'est le décalage vers le rouge z. De façon totalement équivallente, ça nous fait mesurer la température de la source du rayonnement plus froide qu'à l'émission. On définit donc une distance de luminosité Dl qui est celle qu'il faut prendre en compte pour savoir combien d'énergie va arriver au récepteur depuis la source. C'est Dl qui nous donne la magnitude de l'objet. La encore c'est très facile à calculer avec le z :
Dl = Da (1+z)²
Ainsi, un objet qui nous parait, d'après sa taille angulaire être situé à mettons Da = 1 Gal avec un z = 6 est situé aujourd'hui à une distance propre Dp = 1 Gal * (1 + 6) = 7 Gal et l'énergie qui nous en parvient est la même que s'il était situé à 1 Gal (1 + 6)² = 49 Gal.
Pour savoir quel est le temps de regard en arrière (ou temps de trajet du photon), il faut intégrer H(t) et cela dépend de la façon dont on paramétrise le modèle d'expansion, fonction du contenu énergétique de l'univers (rayonnement, matière, constante cosmologique et courbure).
Ci-dessous tu as une abaque avec les paramètres actuels qui te donne la correspondance entre ces différentes notions (source).
Parcours Etranges
Merci à tous pour vos explications.
Un civet, un plat de côtes et puis, glissez-moi une petite paupiette avec.( Lino Ventura)
Après si on veut aller plus loin et savoir par exemple comment on détermine le temps de regard en arrière du photon ou la distance comobile, Gigamesh nous l'explique en détail ici (posts #4 et #6 )
On y trouve des trucs simples : "Si on observe une galaxie à un redshift de z=7, ça veut dire que depuis que cette galaxie a émis cette lumière, l'univers a grandit d'un facteur 1+z = 8."
et des formules plus compliquées mais qui sont les bases du modèle de FLRW
