dimensionnement treillis spatial

[gotrek]

Bonjour,

dans le cadre d'un projet d'étude, je dois présenter une dimensionnement d'un treillis spatial (tridimensionnelle).

Je n'arrive pas à trouver de canevas afin de realiser mon dimensionnement manuelement.

pouvez vous m'aider

gotrek
-----

[verdifre]

tu écris l'équilibre de chaque barre et tu arrives à un gros système d'équations.....

[gotrek]

heu..

peux tu etre un peu plus clair.. je ne vois pas par ou commencer..

dans les structure plane, je calcule l'effort normale dans chaque barre, puis je dimensionne à partir des plus grande valeur ..

ici comment arriver à trouver l'effort dans une barre qui est dans un autre plan .. ?

si tu as un exercice et sa resolution ça m'aiderai bcp. le net est truffé de bonne chose mais il faut encore les trouver !

merci à toi

[verdifre]

plutot que d'écrire deux equations en X et en Y , tu en écrit 3 en X en Y et en Z.
fred

[A voir en vidéo sur Futura]

[gotrek]

au cours, nous avons dimensionner une poutre treillis isostatique avec une charge donée et les information de distance. En aplliquant les charges sur les noeuds supéreiur et en faisant l'équilibre des forces, on pouvait trouver une valeur dans chaque barre qui correspondait à l'effort N.
Ensuite on pouvais dimensionner les membrures ainsi que les montant et diagonales. il s'agissait d'une poutre de type Pratt.

est ce qu'avec ces bases cité ci dessus, je peux être capable de dimensionner un treillis tridimensionnel isostatique ?

je suis désolé mais je ne comprend le système d'équation...

je recherche un type d'exemple basique (simple ) pour avoir une base, un canevas..

merci bcp

[verdifre]

met ton exercice en pièce jointe pour pouvoir en discuter

[gotrek]

en pièce jointe l'exercice avec la poutre treillis,

l’idée c'est de pouvoir réaliser le même type d'exercice avec une structure tridimensionnelle.. j'imagine que le plus simple c'est une poutre tridimensionnelle et non un treille tridimensionnelle

voici la structure que je pense utiliser afin d'illustrer les structures tridimensionnelles

51a5c43cb94c4.jpg

[verdifre]

l'image que tu donnes n'est pas un treillis isostatique

[gotrek]

oui ce n'est pas un treilli mais je me dit que c'st peut etre plus facile à dimensionner avec ce genre de poutre tridimensionelle ?

[gotrek]

le principe de exercice c'est de pouvoir illustrer les structure tridimensionnelle métalique par un exemple de dimensionnment. je cherche alors la structure la plus simple .. et isostatique.. je ne sais pas si j'ai toute les connaissances ce type de dimensionnement sachant que la matière s'est arrêter à la poutre treilli en plan...

[verdifre]

tu peux partir d'un treilli isostatique du type

si tu part du noeud 5, il est aisé de retrouver les efforts dans toutes les menbrures qui arrivent au noeud 5
aprés il faut remonter de proche en proche

[gotrek]

ta pièce jointe est toujours en attente de validation ..

[gotrek]

donc si je pars avec une poutre tridimensionnelle de ce type appuies par les deux noeuds au extrémité, avec les liaison adéquate (un rouleau et une articulation) j'obtiens un système isostatique.. c'est maintenant que cela ce complique..
pour dimensionner, comment faire le lien entre les différents plans ? comment integrer cela dans mes calcul par rapport au cacul d'un treillis plan ?

[Antoane]

Bonsoir.
Merci de représenter la pj sous un format image (png, jpg. ..), plus commode que le pdf.

[gotrek]

structure tridimensionnelle

[verdifre]

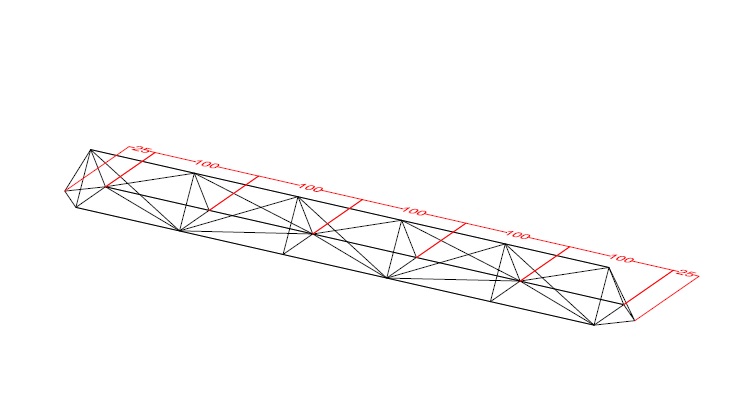
tu fait l'équilibre des noeuds
tu sait que dans une barre, les efforts ne peuvent être que dans la direction de la barre (chaque barre n'est soumise qu'a deux forces)

[verdifre]

Pièce jointe 313551 tu fait l'équilibre des noeuds
tu sait que dans une barre, les efforts ne peuvent être que dans la direction de la barre (chaque barre n'est soumise qu'a deux forces)
Par exemple si on fait l'equilibre du noeud 5

tu peux écrire M +F5_13 + F5_6 + F5_4 =0 sous forme vectorielle bien entendu
c'est l'équilibre du noeud, la somme des forces qui agissent sur le noeud est nulle
à l'aide du repere sur le dessin tu écris les composantes de ces différentes forces.
tu obtient un système de 3 équations à 3 inconues que l'on sait normalement résoudre

[gotrek]

je n'arrive toujours pas a voir ton image...

[verdifre]

c'est la même que celle que j'avais posté précedement

[gotrek]

si je tente de resoudre la premier coupe, avec M et les trois barre qu'il s'y rapporte, j'obtiens

-M+ F13_5 . sin 45° = 0
-f13_5 . cos 45°- f4_5= 0
_f13_5 . cos45° - f5_6 = 0

?

[verdifre]

tu connais M, c'est une donnée du problème, cela te permet de determiner F13_5 facilement et ainsi de suite

si ton treilli est isostatique tu peux determiner de proche en proche l'ensemble de tous les efforts dans les barres

ps dans un cas aussi simple il ne faut pas hésiter à utiliser les symétries

[gotrek]

bien sur, je dois determiner mes charger au appuis et les charges vertical de la toiture. mais mon raisonnement est le bon ?
je me pose la question car la barre f13-5 n'est pas dans le meme plan que la F 4-5 ?


merci

[verdifre]

accesoirement F13-5 est bien dans le même plan que F3-5 défini par les 3 points 13,3,5

mais il ne faut pas se focaliser la dessus
dans le cas du treillis, ou les noeuds sont assimilés à des rotules, le principe fondamental de la statique appliqué au noeud dit que la somme vectorielle de toutes les forces appliquées au noeud est nulle pour que celui ci soit à l'équilibre.
il n'est pas question de plan ou de quoique ce soit d'autre et c'est vrai quelque soit le nombre de dimensions.

la version complete du principe de la statique fait en plus intervenir la somme des moments qui doit être nulle aussi
fred

[gotrek]

autrement dit c'est bien plus complexe qu'une poutre treillis isostatique sur 2 appuis...
je suis pas sorti de l'auberge

mais merci pour ton aide

[verdifre]

ce n'est pas necessairement beaucoup plus compliqué et dans un grand nombre de cas les symétries simplifient grandement le calcul. Il faut être à l'aise en trigo et avec les systèmes d'équations et le reste suit

[gotrek]

lors de nos dimensionnement de poutre treillis plan au cours, nous ne tenions compte que de l'effort normal (traction et compression)
Est ce une étude simplifier (car bachelier en construction) et donc on ne tiens pas compte des moments ?
puis je appliquer exactement le même principe à la poutre tridimensionnelle ?

dans ce quand je commence a comprendre le principe.. je vais tenter un dimensionnement !

[verdifre]

oui, c'est exactement cela, tu considères en 3d que chaque liaison est une rotule, sur une rotule, les moments sont par définition nuls, on ne s'en occupe donc pas
bon courage

[geagea]

bonjour
vous ne pouvez pas le faire manuelelment,le calcul est fastidieux et source d'erreur a chaque noeud vous avez 6 inconnues,actuelelment le calcul se fait en machine,calcul aux éléments finis

cordialement

géagéa

[gotrek]

pouvez vous etre un peu plus claire ? je ne sais pas vraiment ...

merci

[gotrek]

comment justifier vous le fait d'avoir 6 inconnues ?