Je tombe dans un trou noir, vois-je mes pieds ?

[Nicophil]

Alors pourquoi les pieds qui subissent des forces de marées méga plus importantes qu’au niveau de la tête

Mais nooooooon !
-----

[Mailou75]

Salut,

Il est dit que nous vieillissons plus vite en haut d’un immeuble qu’en bas, sans parler des corrections des satellites GPS dues à une gravitation moins importante.

Alors pourquoi les pieds qui subissent des forces de marées méga plus importantes qu’au niveau de la tête, ce principe ne s’appliquerait pas ? qui est que le temps au niveau des pieds « s’écoulerait » moins vite qu’au niveau de la tête ?

D’abord, pour les deux observateurs en haut et en bas de l’immeuble le cas n’est pas comparable puisqu’ils sont tous deux accélérés pour maintenir une altitude constante (ca se traduit par le poids sur une balance) ET ils ne subissent pas la même accéleration (tu pèseras moins lourd en haut de l´immeuble), c’est pourquoi il y a une difference dans l’ecoulement de leur temps.

Ensuite les forces de marée ne sont pas l’effet decrit plus haut comme le laisse entendre ton message, c’est la différence d’effet entre deux points (haut et bas de l’immeuble). En tombant sur Terre tes pieds subissent un plus forte accéleration (etirement radial) et ils sont compressés car la chute n’est pas parallèle mais concentrique vers le centre de la Terre (ton corps prend une forme de triangle avec la pointe vers les pieds). Juste pour le vocabulaire.

Enfin, pour répondre à la question initiale ou plutot ne pas repondre... j’ai regardé et il n’est pas evident qu’en chute libre la tete et les pieds se désynchronisent (plus qu’ils ne le sont déjà) sur le long terme, mis a part l’effet de ta taille (distance propre) entre deux positions. Il y a evidement une distorsion visuelle au passage de l’horizon mais la tête et les pieds atteignent la singularité avec un intervalle de temps propre egal depuis les points desquels ils sont partis. Je ne sais pas trop mais je trouve la question croustillante !

Mailou

[invite69d38f86]

Il y a evidement une distorsion visuelle au passage de l’horizon

Mais pas que. Je dirais plutot qu'il y a une distorsion tout au long de sa chute libre vers le trou noir, mais que rien de spécial ne lui apparait au moment ou il traverse l'horizon.

[bernarddo]

Les trous noirs ont été conceptualisé physiquement uniquement parce que le développement mathématique (métrique de Schwarzschild) l'imposait. C'est comme ça que le concept est apparu. Personne n'en avait besoin, personne ne les a intuitionné dans toute leur bizarrerie.
.

Encore faudrait-il se mettre d'accord sur QUELLE métrique de Schwartzchild ? Il y en a deux, dont une seule, la seconde, est valable à l'intérieur d'un objet massif étendu comme le resterait un trou noir.
Et, à ma connaissance, Schwarzchild n'a jamais parlé de trous noirs.

Or la théorie des trous noirs s'appuie sur la première, qui n'a pas de symétrie centrale, donc pas de centre, tant que le R de la métrique est considéré comme une COORDONNEE VRAIE donc un NOMBRE REEL et pas imaginaire.
D'où les trous noirs n'ont pas d'intérieur, on est en dehors de l'espace-temps.
C'est mathématique.

La question initiale n'est donc pas de savoir si on peut voir ses pieds à l'intérieur d'un trou noir, mais pourquoi les trous noirs sont encore considérés comme réels et parties de l'espace-temps.

[invitee6f0086a]

Merci,

Je crois avoir compris l’élément qui me manqué, par rapport au « vieillissement » en haut et en bas d’un immeuble : dans le trou noir on est en chute libre…

Dans ma question initiale #1 je ne prenais pas en compte le spaghettification. Par contre dorénavant je la prends en compte, et je me repose la question comme quoi les pieds vieillissent (ou pas) plus vite que la tête.

PS : j’utilise mes mots à moi, à remettre dans l’ordre,

Je tombe donc les pieds en avant le TN, et mes pieds sont à 1000kms (pourquoi pas) de ma tête, et de plus, ma structure corporelle est toujours intacte, et même pas mal…

Le delta de gravitation est tout de même conséquent : la montre que j’ai à la cheville bas-t-elle au même rythme que la montre que j’ai autour de la tête ?

J’ai appris ici que la singularité n’est pas un lieu mais un futur, ce qui va dans le sens que la tête vieillit plus vite que les pieds ... !??!...

il serait surprenant qu’il y ait une barrière future/ « présent » instantanée.

Que dissent les maths dans ce cas ?

[Deedee81]

Salut,

Encore faudrait-il se mettre d'accord sur QUELLE métrique de Schwartzchild ? Il y en a deux, dont une seule, la seconde, est valable à l'intérieur d'un objet massif étendu comme le resterait un trou noir.

Je n'en connais qu'une. Tu pourrais écrire les deux métriques ? (ou donner un lien)

[bernarddo]

La formule intérieure a été délivrée dans l'article intitulé:
Über das Gravitationsfeld einer Kugel aus incompressibler Flüssigkeit nach das EINSTEINschein Theorie

Paru 24 Fev 1916



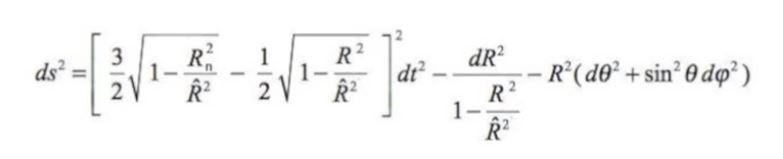
(La formule classique venait de l'article:
Über das Gravitationsfeld eines Massenpunktes nach das ...

Parue 13 Jan 1916

Je suis en train de lire le bouquin de Hawkings "Une brève histoire du temps" (La traduction n'est pas fameuse...)
Dans l'édition Champs science, à la page 150, ce qui est rigolo, c'est qu'il présente un argument qui permet aux trous noirs de contrer le second principe de la thermodynamique, sans bien se rendre compte qu'il devrait plutôt s'agir d'un argument CONTRE les trous noirs. Je cite:

"si un trou noir se trouve aux environs, il semble qu'il y ait une façon encore plus facile de violer ce second principe [de la thermo]: il suffira d'y envoyer un peu de matière douée d'un peu d'entropie, comme une boîte (sic) de gaz. L'entropie à l'extérieur du trou noir diminuera."

Et, en 1988 où il écrit le livre, il se déclare sûr à 95% que Cygnus X-1 était un trou noir.

Il me semble qu'il y a matière à ne pas diaboliser ceux qui renversent la probabilité.

[Mailou75]

Salut,

La formule intérieure a été délivrée dans l'article intitulé:
Über das Gravitationsfeld einer Kugel aus incompressibler Flüssigkeit nach das EINSTEINschein Theorie

Paru 24 Fev 1916

Pièce jointe 364188

Extrèmement interessant ! Quelqu’un est il capable de mettre ça sous la forme t(r)=? (ou r(t))=?) pour l’espace de l’obs à l’infini, un rayon lumineux et une chute libre depuis l’infini (ou mieux depuis R donné) ? Histoire de voir à quoi ça ressemble et comparer les deux versions.

Merci

PS : Dans la premiere version quand la tete atteint la singularité elle voit les pieds qui ne sont pas encore arrivés. Qu’en sera t il dans la seconde version ?

[pm42]

sans bien se rendre compte qu'il devrait plutôt s'agir d'un argument CONTRE les trous noirs. Je cite:

Oui, il est connu pour avoir fait ce genre d'erreur parce qu'il n'était pas très malin Heureusement, il y a des grands physiciens comme toi qui en lisant ses livres de vulgarisation, pas ses articles, arrivent à la corriger

Et, en 1988 où il écrit le livre, il se déclare sûr à 95% que Cygnus X-1 était un trou noir.

Et rien n'a changé depuis 1988 ?

Il me semble qu'il y a matière à ne pas diaboliser ceux qui renversent la probabilité.

Ah, la théorie perso du type qui va nous expliquer que les trous noirs n'existent pas et que Virgo/Ligo ont en fait détecté le passage du métro...
Ca faisait longtemps.

[Mailou75]

Ah, la théorie perso du type qui va nous expliquer que les trous noirs n'existent pas et que Virgo/Ligo ont en fait détecté le passage du métro...

Vraissemblablement il s’agit de la formule pour l’interieur d’un trou noir, rien qui ne contredit tout ce qu’on saura en mesurer de l’exterieur. On est dans le domaine de la spéculation «au dela d’un horizon*visible» avant de prouver qu’il a tort il faudra que tu sautes et nous n’aurons plus de nouvelles de toi

[pm42]

Vraissemblablement il s’agit de la formule pour l’interieur d’un trou noir

Depuis, on parle d'autre chose. Voir "argument contre les trous noirs".

Au demeurant, ses affirmations du genre "D'où les trous noirs n'ont pas d'intérieur, on est en dehors de l'espace-temps. C'est mathématique" étaient déjà du nawak notamment en se limitant à la métrique de Schwartzchild. Tu as participé à assez de fils pour savoir qu'on a un peu progressé depuis.

[Mailou75]

Effectivement, pas bien compris l’absence de symétrie mais j’approuve l’absence de singularité «Newtonnienne» (le massenpukte purement théorique).

[papy-alain]

S'il m'arrive un jour de tomber dans un trou noir, j'aurai d'autres préoccupations que d'essayer de voir mes pieds.

[0577]

Bonjour,

la "métrique intérieure de Schwarzschild" (dérivée par Schwarzschild en 1916) est la métrique à l'intérieur d'une boule de fluide incompressible.
C'est une bonne approximation de la métrique à l'intérieur d'une étoile. Cette métrique n'est valable que si le rayon de la boule est >9/8 du rayon de Schwarzschild: sinon, la pression du fluide au centre de la sphère devient infinie, ce qui est physiquement impossible. Cela signifie qui si une boule de matière passe sous cette limite, les équations d'Einstein n'ont pas de solution statique et rien ne peut empêcher l'effondrement gravitationnel total et la création d'un trou noir.

La "métrique intérieure de Schwarzschild" n'est donc pas la métrique à l'intérieur du trou noir de Schwarzschild. La métrique "à l'intérieur" (i.e. sous l'horizon) du trou noir de Schwarzschild est une solution des équations d'Einstein dans le vide et ne peut se décrire correctement qu'avec des coordonnée adaptées
(comme les coordonnées de Kruskal–Szekeres).

[bernarddo]

Oui, il est connu pour avoir fait ce genre d'erreur parce qu'il n'était pas très malin :
.

C'est le problème (ou l'intérêt) du commentaire en direct. Depuis j'ai avancé de quelques pages, et il a effectivement rectifié le tir: il lui fallait donc trouver une émission pour rattraper le coup.

D'où (après quelques voyages chez les confrères) la nécessité où il s'est trouvé de recourir à la mécanique quantique, pour, via la fluctuation, trouver la possibilité d'émettre quand même d'un endroit qui ne doit rien laisser échapper.
C'est bien le coeur du bouquin et qui a le mérite d'expliquer tout le sens de sa démarche, et tout son développement ultérieur sur le temps "imaginaire", celui dont Schwarzchild n'avait pas besoin, qui considérait un monde réel et prenait son marqueur d'espace R strictement positif, comme celui du temps.
La phrase centrale de Hawkings censée convaincre mériterait que l'on s'y arrête un peu:
"[Ce] temps [imaginaire]paraît appartenir à la fiction mais c'est un concept mathématique bien défini."
est une affirmation fausse: ce qui est défini mathématiquement c'est seulement le nombre imaginaire, le temps est un concept physique, au moins dans le cadre de la RG dans laquelle il est uniquement question de sa mesure.

Et si on peut prendre le métro dans ses rêves, personne n'a pu éditer l'indicateur des ses horaires imaginaires

[0577]

Le "temps imaginaire" auquel Hawking fait référence n'a rien à voir avec les quantités imaginaires qui apparaissent lorsqu'on commet l'erreur d'utiliser des coordonnées inadaptées pour décrire la métrique de Schwarzschild. Dans la description d'un trou noir par la RG, toutes les quantités mesurables de longueur et de temps sont bien entendu des nombres réels. Le "temps imaginaire" est une technique mathématique (prolongement analytique) pour effectuer certains calculs en théorie quantique (les phénomènes d'effet tunnel, qui ont lieu dans le monde réel avec un temps réel, peuvent se calculer à l'aide de solutions de systèmes classiques vivant dans un monde imaginaire avec un temps imaginaire. Ce n'est qu'une astuce de calcul, élémentaire et bien connue. Une des contributions originales de Hawking est l'application de cette astuce de calcul à des particules quantiques se déplaçant sur l'espace-temps courbe de la RG).

[invitee6f0086a]

S'il m'arrive un jour de tomber dans un trou noir, j'aurai d'autres préoccupations que d'essayer de voir mes pieds.

Moi, je sais ce que je ferais :

Je prends une clop, celle-ci fera rapidement des millions de kms de longueur, et de plus le bout sera dans le futur ; de quoi m’occuper un bon bout de temps ! par contre je ne saurais peut-être pas si elle est toujours allumée .

Pardon,

[Mailou75]

Salut,

Cela signifie qui si une boule de matière passe sous cette limite, les équations d'Einstein n'ont pas de solution statique et rien ne peut empêcher l'effondrement gravitationnel total et la création d'un trou noir.

Peut être ne faut il plus appliquer ces équations dans un domaine qui n’est plus physique ?

La "métrique intérieure de Schwarzschild" n'est donc pas la métrique à l'intérieur du trou noir de Schwarzschild. La métrique "à l'intérieur" (i.e. sous l'horizon) du trou noir de Schwarzschild est une solution des équations d'Einstein dans le vide et ne peut se décrire correctement qu'avec des coordonnée adaptées
(comme les coordonnées de Kruskal–Szekeres).

Les coordonnées de Schwarzschild sont parfaitement adaptées à décrire sa solution. Les coordonnées reportées à l’infini le sont tout autant chez Kruskal, c’est une illusion de continuité pour les trajectoires, un point sur l’horizon a toujours pour coordonnée t=infini, il n’est pas défini puisque U et V dépendent de t. Sinon je veux bien ta formule

[0577]

Peut être ne faut il plus appliquer ces équations dans un domaine qui n’est plus physique ?

En quoi ce domaine n'est-il plus physique?

Les coordonnées de Schwarzschild sont parfaitement adaptées à décrire sa solution. Les coordonnées reportées à l’infini le sont tout autant chez Kruskal, c’est une illusion de continuité pour les trajectoires, un point sur l’horizon a toujours pour coordonnée t=infini, il n’est pas défini puisque U et V dépendent de t. Sinon je veux bien ta formule

Il me semble que ces questions ont été discutées de nombreuses fois sur ce forum. Les coordonnées de Schwarzschild sont adaptées à condition de faire les choses correctement (voir par exemple le texte d'Amanuensis à http://forums.futura-sciences.com/ph...arzschild.html) Le résultat final (la géométrie intrinsèque, indépendente des coordonnées) coincide bien sûr avec celui donné par les coordonnées de Kruskal ou autre.

En coordonnées de Kruskal (voir par exemple https://en.wikipedia.org/wiki/Kruska...es_coordinates, l'horizon est défini par U=0 ou V=0. En particulier, les coordonnées U et V sont parfaitement finies à l'horizon. La transformation reliant les coordonnées (r,t) de Schwarzschild aux coordonnées U et V de Kruskal n'est valable qu'à l'extérieur de l'horizon. Si on essaye de prendre une limite à l'horizon, il faut faire attention: U et V dépendent de t, qui tend vers l'infini, mais dépendent aussi de r-2GM, qui tend vers zéro. Pour avoir une limite bien définie, il faut faire un choix de dépendence entre r et t.

[Mailou75]

Salut,

En quoi ce domaine n'est-il plus physique?

Peut etre qu’un trou noir ça n’existe pas ? Je me demandais ce que serait un objet de 1,125.Rs... une etoile a quarks qui enverrait des rayons hautement energetiques et donc identifiable ou un objet si reshifté qu’on ne le verrait pas plus qu’un trou noir (s’il en est) ?

U et V dépendent de t, qui tend vers l'infini, mais dépendent aussi de r-2GM, qui tend vers zéro. Pour avoir une limite bien définie, il faut faire un choix de dépendence entre r et t.

Sans doute un peu hors sujet ici, ma faute... je ne vois pas ce que serait cette dependance et un objet sur l’horizon a une coordonnée t égale a l´infini (pas qui tend vers) et je ne vois pas comment obtenir un resultat chiffré pour U et V. Bien sur que les trajectoires int et ext se raccordent au poil sur la droite a 45°, mais le point exact de contact n’existe pas mathematiquement pour moi, c’est pourquoi je parle d’illusion (bien que dans mon fort interieur je pense plutot «arnaque mathemathique»). Ne pas prendre mal je discute... pour tout te dire, il parrait qu’il existe des coordonnées de Kruskal qui ne dependent pas de r et t et qui pourraient etre continues, mais je n’en dispose pas.

Merci

[0577]

Bonjour,

Je me demandais ce que serait un objet de 1,125.Rs... une etoile a quarks qui enverrait des rayons hautement energetiques et donc identifiable ou un objet si reshifté qu’on ne le verrait pas plus qu’un trou noir (s’il en est) ?

Il est exact que l'on connaît mal l'équation d'état de la matière à des densités extrêmement élevées. Mais cela n'a pas d'importance pour l'argument: quelque soit l'équation d'état de la matière (dans les limites larges imposées par la théorie quantique des champs), la relativité générale prédit que l'effondrement gravitationnel ne peut être stoppé. C'est la raison pour laquelle cet argument est robuste: il ne dépend pas de détails de physique des particules que l'on ignore.

je ne vois pas ce que serait cette dependance et un objet sur l’horizon a une coordonnée t égale a l´infini (pas qui tend vers) et je ne vois pas comment obtenir un resultat chiffré pour U et V. Bien sur que les trajectoires int et ext se raccordent au poil sur la droite a 45°, mais le point exact de contact n’existe pas mathematiquement pour moi, c’est pourquoi je parle d’illusion (bien que dans mon fort interieur je pense plutot «arnaque mathemathique»). Ne pas prendre mal je discute... pour tout te dire, il parrait qu’il existe des coordonnées de Kruskal qui ne dependent pas de r et t et qui pourraient etre continues, mais je n’en dispose pas.

La seule arnaque mathématique ici est d'écrire: "t=infini". Cette expression n'a pas de sens mathématique (contrairement à l'expression "t tend vers l'infini"). L'horizon est juste en dehors de la carte décrite par les coordonnées (r,t). Un exercice intéressant est de considérer une particule en chute libre. Lorsque cette particule s'approche de l'horizon, r tend vers 2GM et t tend vers l'infini, mais r et t ne sont pas des variables indépendantes mais reliées par l'équation de la trajectoire. Le calcul exact est sans doute délicat mais un calcul approché donne

avec c=1 et où C est une constante positive dépendant des conditions initiales. En utilisant cette relation, il est facile de voir que les formules donnant les coordonnées de Kruskal en fonction de r et t ont une limite parfaitement finie lorsque t tend vers l'infin.

[Deedee81]

Salut,

Intéressant. Merci.
Un petit point d'histoire que je ne connaissais pas.

Si j'ai le temps je regarderai plus en profondeur demain.

[Mailou75]

Salut et merci,

Il est exact que l'on connaît mal l'équation d'état de la matière à des densités extrêmement élevées. Mais cela n'a pas d'importance pour l'argument: quelque soit l'équation d'état de la matière (dans les limites larges imposées par la théorie quantique des champs), la relativité générale prédit que l'effondrement gravitationnel ne peut être stoppé. C'est la raison pour laquelle cet argument est robuste: il ne dépend pas de détails de physique des particules que l'on ignore.

Je vais te croire sur parole

La seule arnaque mathématique ici est d'écrire: "t=infini". Cette expression n'a pas de sens mathématique (contrairement à l'expression "t tend vers l'infini"). L'horizon est juste en dehors de la carte décrite par les coordonnées (r,t). Un exercice intéressant est de considérer une particule en chute libre. Lorsque cette particule s'approche de l'horizon, r tend vers 2GM et t tend vers l'infini, mais r et t ne sont pas des variables indépendantes mais reliées par l'équation de la trajectoire. Le calcul exact est sans doute délicat mais un calcul approché donne

avec c=1 et où C est une constante positive dépendant des conditions initiales. En utilisant cette relation, il est facile de voir que les formules donnant les coordonnées de Kruskal en fonction de r et t ont une limite parfaitement finie lorsque t tend vers l'infini.

Il faudrait que je regarde ce que donne ta formule, je suis d’accord sinon, c’est le mot souligné qui m’ennuie. En utilisant les formules classiques de Kruskal un point strictement sur l’horizon devra avoir pour coordonnée t=inf sinon c’est qu’il sera a coté (tendre vers) et ça pose tout le problème du raccord «illusoire» entre les zones I et II de Kruskal. J’avais consulté le document d’Amanuensis que tu as link, c’est tout le sujet de ce point etiré. Il avait lui meme imaginé un système compact mettant en evidence le point de passage obligatoire de toutes les trajectoires à (Rs;+/-infini) (voir http://forums.futura-sciences.com/as...ml#post5943643) Je suis donc perplexe

.....

Ceci ravive une vielle question, simple, fondamentale et perturbante quant aux choix pris sur les «axiomes»... j’en profite, peut être auras tu une explication?

Si on prend par exemple Painlevé et Schwarzschild, on voit que la droite/courbe t=0 (cad l'espace synchronisé de l'observateur éloigné à t=0) arrive à la même coordonnée verticale, normal jusqu'ici puisque c'est la référence choisie. Ce qui est plus étonnant c'est que pour t=Rs/c, la droite se décale d'une "unité" (a-dimensionné Rs/c=1) vers le haut chez Schwarzschild et AUSSI d'une unité chez Painlevé. Pourtant sur un axe on lit t et sur l'autre . Représenter ceci revient à admettre que d'une certaine façon t= ?!

Merci

Mailou

[Zefram Cochrane]

Bonjour,
Si je prends un coton tige et je mets une boule au milieu.
La vitesse de chute de chaque extrémité du coton tige sera celle de la boule telle qu'elle sera perçue par chaque extrémité.
Donc si je me place du point de vue de l'extrémité basse du coton tige à l'instant où il traverse l'horizon du TN, il verra la boule avec une vitesse < c donc sa vitesse de chute sera inférieure à c.
Si je me place du point de vue de l'extrémité haute du coton tige. Il ne verra la boule avoir une vitesse égale à c, ie à l'instant ou il traverse le TN qu'à l'instant même où lui même traversera l'horizon du TN.

Conclusion : Lorsque mes pieds traversent l'horizon du TN, je les vois.

P.S On a jamais fais l'étude dans laquelle on est en chute libre avec une vitesse supérieure à la vitesse de libération.

[invitee6f0086a]

J’ai du mal à saisir la frontière de l’horizon des évènements, frontière ou les photons sont piégés et ne sortent plus du TN.

Vous dites que pour l’astronaute, il ne sentira pas le passage de cette frontière et qu’il verra toujours ses pieds (il tombe les pieds en avant pour rappel).

J’ai une petite question :

Mon astronaute a un très long bâton avec au bout une méga lampe torche, et il tombe dans le TN le bâton en avant.

Dans sa chute, y-a-t-il un moment ou il ne verra plus la lumière au bout du bâton ?

Je me dis qu’à un moment donné les photons n’auront « plus de force/énergie…) pour remonter vers l’astronaute.

Vous en pensez quoi ? Merci,

PS : j’exclus un décalage vers le rouge et autres, mon astronaute a des lunettes et « voit » dans tous les spectres. Des rayons gamma aux ondes radios, et au delà.

[bernarddo]

Bonjour,

la "métrique intérieure de Schwarzschild" (dérivée par Schwarzschild en 1916) est la métrique à l'intérieur d'une boule de fluide incompressible.
C'est une bonne approximation de la métrique à l'intérieur d'une étoile. Cette métrique n'est valable que si le rayon de la boule est >9/8 du rayon de Schwarzschild: sinon, la pression du fluide au centre de la sphère devient infinie, ce qui est physiquement impossible. Cela signifie qui si une boule de matière passe sous cette limite, les équations d'Einstein n'ont pas de solution statique et rien ne peut empêcher l'effondrement gravitationnel total et la création d'un trou noir.

La "métrique intérieure de Schwarzschild" n'est donc pas la métrique à l'intérieur du trou noir de Schwarzschild. La métrique "à l'intérieur" (i.e. sous l'horizon) du trou noir de Schwarzschild est une solution des équations d'Einstein dans le vide et ne peut se décrire correctement qu'avec des coordonnée adaptées
(comme les coordonnées de Kruskal–Szekeres).

Bonjour,
enfin une discussion qui va pouvoir s'engager sur du concret !
Une métrique "intérieure" est valable par définition, à l'intérieur d'un rayon.
Si la métrique intérieure a un problème à 9/8 du rayon de Schwarzchild, c'est donc qu'elle est valable au delà. Elle prend donc le relais de la métrique extérieure AVANT que l'effondrement n'atteigne le rayon de Schwarzchild. Pour cette valeur (9/8), la pression au centre de l'étoile devient infinie.
Nous ne sommes plus devant une singularité MATHEMATIQUE, mais devant une singularité PHYSIQUE, qui rend caduque la singularité qui a engendré le concept de trou noir liée à l'utilisation de la métrique extérieure, fautive dans ce cas puisqu'elle est liée à un point-masse alors qu'on est dans le cas d'une masse étendue.
Hawking connaissait la solution intérieure puisque, page 129 de son livre, il parle d'Oppenheimer (et connaissait donc la formule TOV qui est équivalente à la solution intérieure) , mais n'a apparemment pas remarqué, ni les autres tenants du trou noir ultérieurs, cet énorme problème, (jusqu'à Abrams).
On ne devrait plus pouvoir ignorer ce problème majeur, ... et basique !

[pm42]

On ne devrait plus pouvoir ignorer ce problème majeur, ... et basique !

On va quand même attendre que tu aies fini de lire ton livre de vulgarisation avant d'être sur que c'est un vrai problème

[Zefram Cochrane]

J’ai du mal à saisir la frontière de l’horizon des évènements, frontière ou les photons sont piégés et ne sortent plus du TN.

Vous dites que pour l’astronaute, il ne sentira pas le passage de cette frontière et qu’il verra toujours ses pieds (il tombe les pieds en avant pour rappel).

J’ai une petite question :

Mon astronaute a un très long bâton avec au bout une méga lampe torche, et il tombe dans le TN le bâton en avant.

Dans sa chute, y-a-t-il un moment ou il ne verra plus la lumière au bout du bâton ?

Je me dis qu’à un moment donné les photons n’auront « plus de force/énergie…) pour remonter vers l’astronaute.

Vous en pensez quoi ? Merci,

PS : j’exclus un décalage vers le rouge et autres, mon astronaute a des lunettes et « voit » dans tous les spectres. Des rayons gamma aux ondes radios, et au delà.

Remplace dans mon exemple le coton tige pas ton long bâton et la boule centrale par Buzz l'éclair

[invitee6f0086a]

Remplace dans mon exemple le coton tige pas ton long bâton et la boule centrale par Buzz l'éclair

Juste pour confirmation, Buzz l’éclair verra bien les deux extrémités du coton tige TOUT LE LONG DE LA CHUTTE ?

[Zefram Cochrane]

Bonsoir,
dans le cas d'une chute libre depuis l'infini où la vitesse de chute de buzz l'éclair est égale à la vitesse de libration (V<Vlib si la chute s'effectue à partir d'une altitude r finie)
Buzz l'éclair voit l'extrémité basse du coton tige atteindre l'horizon du TN lorsque lui-même atteint l'horizon du TN et lorsqu'il atteint l'horizon du TN, il voit l'extrémité supérieure du coton tige.

Une question intéressante serait de savoir ce qu'il se passe si après avoir accéléré en direction du TN pour avoir une vitesse V>Vlib à une distance r>> Rs. est ce que la vitesse V peut devenir >c alors que Buzz l'éclair n'a pas atteint l'horizon du TN? comment cela se passe au niveau de l'effet marée?