Durée effective RR

[tierri]

Pour Bleu :
Durée du trajet aller 54ans. Distance aller parcourue 24 AL
Durée du trajet retour 6 ans Distance retour parcourue 24AL
Durée aller -retour 60ans. Distance franchie 48AL

OK, donc nous avons là le relevé direct de ce que voit Bleu quand il observe les photons émis par Rouge.

Pour Bleu :

- à l'aller la vitesse apparente vaut 24AL/54ans=0,44c

- au retour elle vaut 24AL/6ans=4c

D'accord, très bien, mais là ou cela devient cornélien c'est avec le point de vue de rouge.
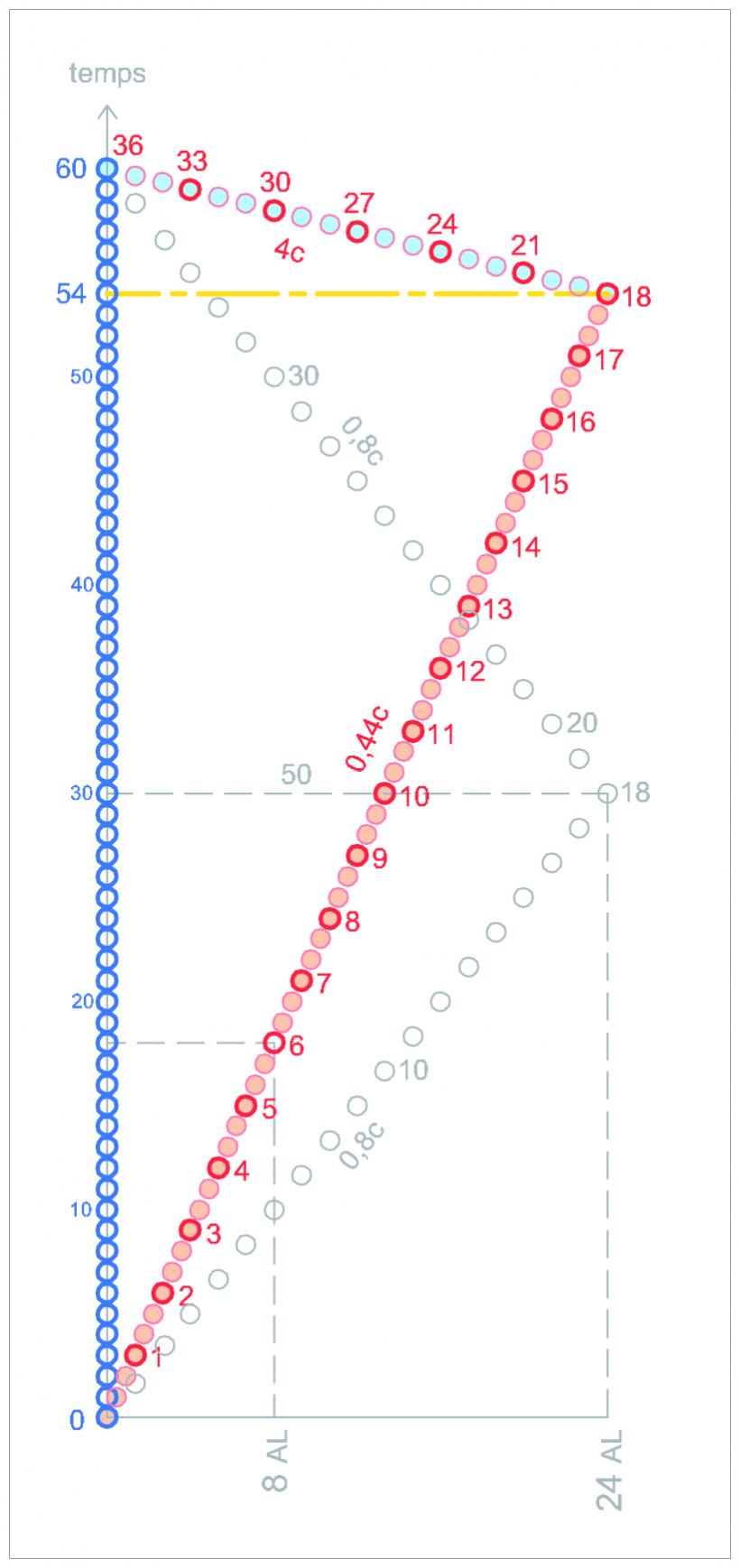
On considère cette fois le point de vue de Rouge qui observe les photons émis par Bleu.
Mais c'est toujours Rouge qui est en mouvement et bleu immobile, ça on ne peut pas le changer, c'est immuable.
Donc on a toujours le même rapport entre les temps propres : TB = 5/3 TR
Quand une seconde s'écoule pour Rouge, 5/3 sec s'écoulent pour Bleu, ou
TR = 3/5 TB
Quand une sec s'écoule pour Bleu, 3/5 sec s'écoulent pour Rouge (plus adapté dans ce cas puisque c'est Bleu qui envoie les signaux lumineux)

Bleu émet des signaux lumineux toutes les secondes, à quel rythme Rouge les reçoit-il, à l'aller et au retour ?
Dans les deux cas on a toujours donc : TR = 3/5 TB
A l'aller, Rouge s'éloigne de bleu, lorsqu'il reçoit un signal il sait que le suivant sera émis 3/5 sec plus tard et lui parviendra 3/5sec plus tard plus le temps nécessaire aux photon pour parcourir le surplus de distance parcouru par Rouge avant que le photon suivant ne le rattrape.
Je trouve 3 s

Au retour Rouge voyage cette fois en direction de Bleu,
On a toujours TR = 3/5 TB
Quand Rouge reçoit un signal il sait que le suivant est émis 3/5 sec plus tard mais aura une plus courte distance à parcourir, il arrivera à Rouge à 3/5sec moins le temps nécessaire au photon pour parcourir une distance équivalente à celle parcourue par rouge avant qu'il ne l'atteigne, je trouve 1/3 s

Que l'on regarde depuis Bleu les signaux émis par Rouge toutes les secondes ou depuis Rouge les signaux émis par Bleu toutes les secondes, on reçois toujours un signal toutes les trois secondes en éloignement et un signal tous les tiers de seconde en rapprochement.

L'effet Doppler relativiste est réversible

MAIS

C'est toujours Rouge qui est en mouvement et il existe bien un référentiel au mouvement privilégié.
-----

[Zefram Cochrane]

Bonsoir,


Je me suis rendu compte d'une petite erreur dans mon mess précédent

La correction


j'avais fait un copié coller d'un mess précédent que j'ai adapté.
Les calculs sont toujours juste.

D'après ton schéma Mailou, je pense que le point de vue de Vert est le suivant :
tu as placé son point de départ à 48 AL de Bleu
En fait Vert verra Rouge quitter Bleu à une date Tb telle que :
C.Tb = 48 AL – 0,8.C.Tb


Soit : avant de rejoindre rouge. Il s'agit présentement d'un temps coordonnée de Bleu
Ce qui correspond en temps propre de Vert à

On aurait pu le retrouver autrement. On sait que sa vitesse relative avec Rouge est de (40/41c) pendant la première période. Ce qui veut dire que du point de vue de Vert, le temps semble s'écouler 9 fois plus vite pour Rouge que pour lui, et donc 18/9 = 2 ans.
Vert s'approche de Bleu à 0,8c, cela veut dire que pour Vert le temps semble s'écouler 3 fois plus vite pour Bleu que pour lui soit : 3*2 = 6ans.
Donc au moment ou Vert rejoindra bleu, il aura vieillit de 20ans et Bleu de 60ans. La vitesse apparente d'approche de Vert est de 4c pendant toute la durée de l'expérience soit une distance apparente franchie de 80AL.

Le point de vue de Bleu à propos de Vert est le suivant. Le point de départ de Vert se trouve à la distance coordonnée normal

Bleu voit Vert partir à la durée effective (160/3)ans; soit (20/3) ans avant d'avoir 60ans. Comme le temps semble s'écouler trois fois plus vite pour Vert que pour lui. Lorsqu'il voit Vert débarquer, Vert à 20ans.

Tes schémas démontrent bien l'absence de référentiels absolus.

J'avoue que tu as une vision plus ascérée du phénomène d'abbération de la lumière je veux bien que tu développes.

Cordialement,
Zefram

[Zefram Cochrane]

Un dernier truc amusant:
Pendant la phase d'approche de Rouge et Vert:
La vitesse apparente d'approche est de 40c.
40*2=80AL

[Zefram Cochrane]

Reprenons
Trajet Aller

Pour Bleu
Tb = 0, Bleu voit s'éloigner Rouge à une vitesse apparente de (4/9)c
Rouge s'éloigne de Bleu pendant une durée Tr = 18 ans.
Le temps semble s'écouler trois fois moins vite pour Rouge que pour Bleu lorsqu'il lit sur l'horloge de Rouge 18ans, Tb = 54ans.
La distance franchie par Rouge est de 54*(4/9) = 6*4 = 24AL

Pour Vert
A Tv=0 Vert voit Rouge s'approcher de lui à une vitesse apparente de 40c
Rouge s'approche de Vert pendant une durée de Tr = 18ans.
Le temps semble s'écouler neuf fois plus vite pour Rouge que pour Vert. Lorsque Rouge rejoint Vert, Tv = 2ans
La distance franchie par Rouge est de 40*2 = 80AL. C'est aussi la distance à laquelle il voit Bleu à Tv = 0

Pour Rouge

Il voit s'éloigner Bleu à une vitesse apparente de (4/9)c
Le temps semble s'écouler trois fois moins vite pour Bleu que pour Rouge. lorsqu'il lit sur son horloge Tr = 18ans, Il lit sur celle de Bleu 6 ans.
La distance franchie par Bleu est de 18*(4/9) = 8AL

Rouge voit Vert s'approcher de lui avec une vitesse apparente de 40c
Lorsqu'il atteint Vert, il lit sur l'horloge de Vert 2ans.
Le temps semble s'être écoulé neuf fois plus vite pour Vert que pour Rouge cela veut dire que Rouge a vu partir Vert à Tr = 18 – (2/9) = (170/9) ans
La distance franchie par Vert est de (2/9)*40 = 80/9 AL

Trajet Retour

Pour Bleu
Tb = 54, Bleu voit s'approcher Rouge à une vitesse apparente de 4c
Rouge s'approchede Bleu pendant une durée Tr = 18 ans.
Le temps semble s'écouler trois fois plus vite pour Rouge que pour Bleu lorsqu'il lit sur l'horloge de Rouge 36ans, Tb =54 + 6 = 60ans.
La distance franchie par Rouge est de 24 AL + 6*4 = 48AL


Vert s'approche de Bleu pendant une durée Tv = 20 ans.
Le temps semble s'écouler trois fois plus vite pour Vert que pour Bleu lorsqu'il lit sur l'horloge de Vert 20ans, Tb = 60ans. Bleu voit vert s'approcher de lui à Tb = 60 – 20/3 = 160/3
La distance franchie par Vert est de (20/3)*4 = (80/3)AL

Pour Vert
A Tv=2 Vert voit Bleu s'approcher de lui à une vitesse apparente de 4c
Bleu s'approche de Vert pendant une durée de Tv = 18ans.
Le temps semble s'écouler trois fois plus vite pour Bleu que pour Vert. Lorsque Bleu rejoint Vert, Tv = 2 + 18 = 20ans Tb= 20*3 = 60ans
La distance franchie par Bleu est de 4*20 = 80AL.

Pour Rouge

Il voit s'éloigner Bleu à une vitesse apparente de 4c
Le temps semble s'écouler trois fois plus vite pour Bleu que pour Rouge. lorsqu'il lit sur son horloge Tr = 36ans, Il lit sur celle de Bleu 60 ans.
La distance franchie par Bleu est de 8 + 18*4 = 80AL

Il devient très difficile d'affirmer que c'est parce que Rouge n'est pas un système de références inertielles qu'il y a disymétrie des observations; car Vert est un système de références inertielles, tout comme Bleu. Une petite analyse complémentaire s'impose.

Cordialement,
Zefram

[tierri]

Tout cela me contrarie et nous pose beaucoup de problèmes, si je me fie à la définition du référentiel inertiel (http://fr.wikipedia.org/wiki/R%C3%A9..._galil%C3%A9en) tu as raison.

Tu considères donc que quand Rouge est en MRU par rapport à bleu, les déformations ne sont qu'apparentes et décrites par l'effet Doppler relativiste dont la réversibilité te conforte dans cet avis, et tu places toutes les déformations réelles dans les phases d'accélération (le rebond de rouge au moment du demi-tour)

J'ai trouvé les mêmes résultats que toi en partant de l'hypothèse que Bleu, sa position et ses métriques d'espace et de temps était le seul référentiel valable pour tout mouvement, m'épargnant tout problème de paradoxe, sans utiliser la formule de l'effet Doppler relativiste.
Maintenant si j'inverse en disant que c'est Rouge le seul référentiel valable, je suis alors vite en conflit avec la première version, il y a paradoxe, mais si je calcule l'effet Doppler relativiste je trouve quand même toujours le même résultat, l'effet Doppler relativiste est réversible et c'est bien là son problème, il ne fait pas la différence.

Et puisqu'il ne fait pas la différence tu ne peux pas te servir de lui pour dire qu'il n'existe pas de référentiel privilégié au mouvement.
S'il y en a un l'effet Doppler relativiste s'y intègrera parfaitement, il n'y a pas de problème.

Puisque l'effet Doppler relativiste ne fait pas la différence tu décides que c'est Rouge qui fait le demi-tour, mais là je me sens obligé de te faire remarquer qu'en ce faisant tu admets le référentiel privilégié sinon comment sais-tu que Rouge accélère ? Par rapport à quoi ? Et toute force qui apparaitrait serait mesuré par rapport à ce même référentiel, quel que soit le chemin suivi on a absolument besoin d'un référentiel privilégié pour le mouvement.

[Mailou75]

Salut,

Que l'on regarde depuis Bleu les signaux émis par Rouge toutes les secondes ou depuis Rouge les signaux émis par Bleu toutes les secondes, on reçois toujours un signal toutes les trois secondes en éloignement et un signal tous les tiers de seconde en rapprochement.
L'effet Doppler relativiste est réversible

Oui

C'est toujours Rouge qui est en mouvement et il existe bien un référentiel au mouvement privilégié.

Tout est réversible entre les référentiels inertiels (vitesse constante) soit Bleu, Rouge et Vert.
Mais le voyageur Rouge emprunte deux référentiels inertiels différents : Rouge à l'aller et Vert au retour, c'est ce changement qui crée la dissymétrie.
Si tu places au hasard deux évènements (départ et arrivée) dans l'espace-temps 4D alors celui qui va tout droit (inertiel) entre ces deux points sera le plus vieux des "jumeaux" (Bleu)
Ceux qui voudront croiser ces deux évènements (pour comparer des horloges) auront deux choix : rester "sur place" avec Bleu ou faire un p'tit tour (Rouge)...
Vraisemblablement le plus jeune des jumeaux n'est pas forcément celui qui ira le plus loin mais celui qui aura subi les plus fortes accélérations

J'avoue que tu as une vision plus acérée du phénomène d’aberration de la lumière je veux bien que tu développes.

Je soulevais juste le problème à cause du "chainon manquant" dans l'histoire de ce que voit Rouge
Ce qui compte dans l'aberration c'est que Bleu n'a pas de "trou dans le temps", lui... Rouge et Bleu comptent le même temps entre émission et réception !
Aller : Bleu émet à 6ans alors que Rouge a 6ans et il a 18ans quand Rouge réceptionne à 18ans. Bleu et Rouge comptent tout les deux 18-6=12ans
Retour : Bleu émet à 6ans alors que Rouge a -18ans et il a 42ans quand Rouge réceptionne à 18ans. Bleu et Rouge comptent tout les deux 42-6=18+18=36ans
Le reste c'est juste une histoire de calendrier, je ne vais pas m'étendre trop dessus car j'ai un post à déterrer (http://forums.futura-sciences.com/as...ml#post4628369).
Le schéma du link n'est pas tout a fait juste (zappé le ...) mais ça donne une idée du principe

Pour le reste des calculs c'est tout bon* à part ceci, corrigé dans le texte
*(sauf que ton origine de Vert se trouve à la réception du signal de départ de Bleu)

Trajet Aller

Pour Rouge
Le temps semble s'être écoulé neuf fois plus vite pour Vert que pour Rouge cela veut dire que Rouge a vu partir Vert à Tr = 18 – (2/9) = 17,77 ans

Trajet Retour

Pour Bleu
Le temps semble s'écouler trois fois plus vite pour Rouge que pour Bleu lorsqu'il lit sur l'horloge de Rouge +18ans depuis boost , Tb =60-54 = +6ans > (18/6=3).

Pour Rouge
Le temps semble s'écouler trois fois plus vite pour Bleu que pour Rouge. lorsqu'il lit sur son horloge Tr = +18ans depuis boost, Il lit sur celle de Bleu Tb=60-6=54ans > (54/18=3)

Il devient très difficile d'affirmer que c'est parce que Rouge n'est pas un système de références inertielles qu'il y a dissymétrie des observations; car Vert est un système de références inertielles, tout comme Bleu. Une petite analyse complémentaire s'impose.

Surtout quand on compare deux référentiels qui se croisent à des ages différents

A+
Mailou

[Zefram Cochrane]

Tu pourrais faire un petit schéma de ce que VOIENT Bleu, Rouge et Vert STP?
Cordialement Zefram

[tierri]

Je pars d'une RR non réversible avec un référentiel privilégié, j'y ajoute de simples considérations géométriques et j'aboutis à l'effet Doppler relativiste.

Rouge est en mouvement et Bleu est immobile.
Dans tous les cas on a toujours : T= To
Quand une seconde s'écoule pour rouge, secondes s'écoulent pour Bleu, quel que soit le sens du déplacement.

Quand Rouge s'éloigne, au moment ou Bleu reçoit un signal il sait que le suivant sera émis secondes plus tard d'un point plus éloigné d'une distance valant vT
Ce qui donne un T perçu par Bleu (Tp) : Tp = T + vT/c = T(1 + v/c) = To(1 + v/c)

Je ne suis pas doué pour écrire des formules mais j'ai fait la démonstration et j'aboutis bien à la formule de l'effet Doppler relativiste pour un objet en éloignement.

Maintenant quand Rouge se rapproche de Bleu
Je dis donc que l'on a toujours T= To
Quand une seconde s'écoule pour rouge, secondes s'écoulent pour Bleu, cela n'a pas changé, une RR NON réversible donc.
Au moment ou Bleu reçoit un signal il sait que le suivant sera émis secondes plus tard d'un point plus proche cette fois d'une distance valant vT
Ce qui donne un T perçu par Bleu (Tp) : Tp = T - vT/c
Et vous l'avez compris, j'aboutis à la formule de l'effet Doppler relativiste pour un objet se rapprochant.

Et je peux poursuivre ainsi avec le point de vue de Rouge quand c'est Bleu qui émet les signaux, considérer toujours Rouge en mouvement et commencer par l'éternel : T= To, et aboutir encore aux formules de l'effet Doppler relativiste.

CONCLUSION :

Un référentiel privilégié pour le mouvement est parfaitement compatible avec l'effet Doppler relativiste.

J'ajoute une petite remarque personnelle :
Je vous invite à faire au moins une des démonstrations afin de le constater par vous-même puis vous poser cette question :

Est-il possible de démontrer l'effet Doppler relativiste autrement ?

[azizovsky]

Est-il possible de démontrer l'effet Doppler relativiste autrement ?

Salut , oui , à partir des TLs :

x'(1)=Y[x(1)-vt(1)]

x'(2)=Y[x(2)-vt(2)]

si (2) est un événement postérieur à (1)

x(2)-x(1)=Y{[x(2)-x(1)]-v[t(2)-t(1)} <==>

l'=Y (l-vT) (a)

avec l et l' longueurs d'ondre et l'=cT' et l=cT (a') on injectons (a') dans (a)

l'=Y (l-vl/c) =Y(1-v/c).l avec Y facteur de Lorentz

T'=Y (l-vl/c) =Y(1-v/c).T

dans le cas contraire ,tu pose v=-u

l'=Y (l+ul/c) =Y(1+/c).l

[tierri]

Salut , oui , à partir des TLs :

x'(1)=Y[x(1)-vt(1)]

x'(2)=Y[x(2)-vt(2)]

si (2) est un événement postérieur à (1)

x(2)-x(1)=Y{[x(2)-x(1)]-v[t(2)-t(1)} <==>

l'=Y (l-vT) (a)

avec l et l' longueurs d'ondre et l'=cT' et l=cT (a') on injectons (a') dans (a)

l'=Y (l-vl/c) =Y(1-v/c).l avec Y facteur de Lorentz

T'=Y (l-vl/c) =Y(1-v/c).T

dans le cas contraire ,tu pose v=-u

l'=Y (l+ul/c) =Y(1+/c).l

J'aurais mieux fait de m'abstenir de poser cette question.

Bon, OK, je ne comprends pas bien mais je n'ai aucune raison de douter pas de la justesse de l'argumentation.

Ma petite démonstration ne prouve pas qu'il y a forcément un référentiel privilégié et une RR non-réversible, mais elle prouve que l'effet doppler relativiste ne permet en rien de l'écarter, ils s'accommodent très bien l'un de l'autre.
Cela me suffit amplement.

[Zefram Cochrane]

Salut,

Le problèmes de tes démonstrations Azizovsky est que vu que tu n'utilise pas le Latex, elles piquent les yeux, c'est un peu comme lire un texte sans espace ni ponctuation.

Voici ma proposition de démonstration :

Soit un stroboscope émettant des pulsations à la fréquence correspondant à la période

pendant un intervalle de temps le stroboscope va émettre N pulsations on a donc

On sait que si le stroboscope s'éloigne à v ( du récepteur sur une distance X ( point de vue du récepteur) .
Il recevra N pulsations également mais un bout d'une durée effective


De même si le stroboscope s'approche à v du récepteur depuis une distance X
Le récepteur recevra N pulsations mais au bout d'une durée effective


Où est le facteur de Lorentz. Disons qu'on ignore l'expression de comment la retrouver?


On a :


et


de même :


donc


D'où :


on a donc

soit

au final :



Il est évident que le récepteur reçoit le même nombre N de pulsations émises par le stroboscope à l'aller qu'au retour. Seulement c'est la fréquence à laquelle il les reçoit qui diffère. Comme la fréquence c'est l'inverse de la période

Si le stroboscope s'éloigne du récepteur à v


Si le stroboscope s'approche du récepteur à v



Maintenant
Si il y avait un référentiel absolu on aurait :
pour un mobile en éloignement
pour un mobile en rapprochement
et on retrouve la relation de l'effet doppler relativiste pour le mobile émettant des pulsations lumineuse en direction de l'observateur stationnaire
Seulement, si c'est l'observateur stationnaire qui émet les pulsations, le mobile recevrait des pulsation telle que :



L'effet n'est donc pas réversible dans le cas de l'existence du référentiel absolu. Quand on commence à s'interresser à la RR, beaucoup on tendance à penser qu'il existe un référentiel absolu défini par v = 0 et que dans tous les autres référentiels en mouvements le temps s'écoule fois moins vite que dans ce référentiel absolu de référence.
C'est un Gap à passer en RR.

Cordialement,
Zefram

[Zefram Cochrane]

Damned , je pense que c'est propre :

Soit un stroboscope émettant des pulsations à la fréquence correspondant à la période

pendant un intervalle de temps le stroboscope va émettre N pulsations on a donc

On sait que si le stroboscope s'éloigne à v ( ) du récepteur sur une distance X ( point de vue du récepteur) .
Il recevra N pulsations également mais un bout d'une durée effective


De même si le stroboscope s'approche à v du récepteur depuis une distance X
Le récepteur recevra N pulsations mais au bout d'une durée effective


Où est le facteur de Lorentz. Disons qu'on ignore l'expression de comment la retrouver?


On a :


et


de même :


ce qui donne :



donc


D'où :


on a donc

soit

au final :



Il est évident que le récepteur reçoit le même nombre N de pulsations émises par le stroboscope à l'aller qu'au retour. Seulement c'est la fréquence à laquelle il les reçoit qui diffère. Comme la fréquence c'est l'inverse de la période

Si le stroboscope s'éloigne du récepteur à v


Si le stroboscope s'approche du récepteur à v



Cordialement,
Zefram

[tierri]

Seulement, si c'est l'observateur stationnaire qui émet les pulsations, le mobile recevrait des pulsation telle que :

NON

Bleu est immobile et envoie des signaux à rouge qui s'éloigne à v

On a toujours : T = To
Quand une seconde s'écoule pour rouge, secondes s'écoulent pour Bleu, comme d'hab
Donc quand une seconde s'écoule pour bleu, 1/ secondes s'écoulent pour rouge
Quand Rouge reçoit un signal il sait que le suivant sera émis 1/ secondes plus tard, qu'à ce moment-là rouge sera vT plus loin et qu'il faudra au photon le temps T' pour le rattraper tel que : vT + vT' = cT'
Tr (T reçu par rouge) = T + T'
J'ai résolu ça et je tombe bel et bien, comme toujours, sur la formule de l'effet doppler relativiste pour un objet s'éloignant.
C'est toi qui te trompe zefram

[azizovsky]

Salut,

Le problèmes de tes démonstrations Azizovsky est que vu que tu n'utilise pas le Latex, elles piquent les yeux, c'est un peu comme lire un texte sans espace ni ponctuation.

Zefram

Bonsoir , désolé ZC , j'aimerai bien utiliser Latex , mais avant ,j'ai appris l'autocad ,PEB ..., à la fin ,rien ne sert dans mon travail .

[Zefram Cochrane]

Tu peux toujours répondre avec citation un de mes mess
Copier coller sur un DOC , bidouiller
Répondre a la discussion
Aller au mode avancé. vérifier tes formules
Après je peux aussi t'ai det
Jnai appris sur le tas même si je ne connais pas tout
Cordialement.Zefram

[azizovsky]

Tu peux toujours répondre avec citation un de mes mess
Copier coller sur un DOC , bidouiller
Répondre a la discussion
Aller au mode avancé. vérifier tes formules
Après je peux aussi t'ai det
Jnai appris sur le tas même si je ne connais pas tout
Cordialement.Zefram

Salut ,un grand merci ZC ,je vais faire un effort .

[Zefram Cochrane]

Reprenons :

NON

Bleu est immobile et envoie des signaux à rouge qui s'éloigne à v

On a toujours : T = To
Quand une seconde s'écoule pour rouge, secondes s'écoulent pour Bleu, comme d'hab
Donc quand une seconde s'écoule pour bleu, 1/ secondes s'écoulent pour rouge
Quand Rouge reçoit un signal il sait que le suivant sera émis 1/ secondes plus tard, qu'à ce moment-là rouge sera vT plus loin et qu'il faudra au photon le temps T' pour le rattraper tel que : vT + vT' = cT'
Tr (T reçu par rouge) = T + T'
J'ai résolu ça et je tombe bel et bien, comme toujours, sur la formule de l'effet doppler relativiste pour un objet s'éloignant.
C'est toi qui te trompe zefram

Pour Rouge; Bleu s'éloigne de lui à v à
au bout d'un temps Tr Bleu s'est éloigné d'une distance du fait du temps mis par la lumière pour parcourir cette distance on a
on a donc
Tr verra Bleu à une distance Xr au bout d'un temps

Si ( à cause du caractère absolu du référentiel de Bleu)
on a donc
Pour Bleu en rapprochement ;

Il doit y avoir une coquille dans ton raisonnement.
Cordialement,
Zefram

[tierri]

au bout d'un temps Tr Bleu s'est éloigné d'une distance du fait du temps mis par la lumière pour parcourir cette distance on a

Rouge s'est éloigné pas bleu, et il continue de s'éloigner, c'est là que tu commets ta confusion.
Quand ton photon a parcouru la distance que tu indiques, rouge n'y est plus.
Tu l'as oublié en route ton photon, il doit rattraper rouge.

[Mailou75]

Salut,

Tu pourrais faire un petit schéma de ce que VOIENT Bleu, Rouge et Vert STP?

Pour Bleu c'est pas spécialement intéressant et Vert oublie le c'est juste un repère, je te fais Rouge

La partie basse est un extrait du précédent dessin pour légitimer ce que je racontais dans mon dernier message :

Aller : Bleu émet à 6ans alors que Rouge a 6ans et il a 18ans quand Rouge réceptionne à 18ans. Bleu et Rouge comptent tout les deux 18-6=12ans
Retour : Bleu émet à 6ans alors que Rouge a -18ans et il a 42ans quand Rouge réceptionne à 18ans. Bleu et Rouge comptent tout les deux 42-6=18+18=36ans

Un truc qui fera peut être plaisir à Amanuensis, qui cherchais une signification aux "surfaces d'espace-temps" :
Le triangle bleu est 9 fois plus grand que le rouge, quel que soit repère !
Et 9 c'est le z+1 de 0,975c soit ce qu'il faut pour passer de -0,8c à +0,8c !!
Le parallélépipède mou que j'ai grisé voit lui aussi sa surface multipliée par 9 entre les deux repères, elle est là la dissymétrie

La partie haute c'est ce que voit Rouge, je t'ai fait des gros objets pour voir la différence entre les angles (distance angulaire).
L'impression que le champ visuel se rétrécit dans la direction du mouvement, l’aberration, c'est ça : l'objet est vu plus loin, plus blueshifté
Note que là on passe de -0,8c (rouge) à +0,8c (bleu) la différence entre les deux positions vues est 72/8=9 ...

Un truc amusant, si on trace la trajectoire réelle de Bleu pour Rouge, aller/retour à 24AL en 18ans, alors il va à , normal...
mais l’échelle de temps sur sa "pseudo ligne d'univers" est la même que celle de Rouge ! , ,

A+
Mailou

[Mailou75]

Et je m'avance pour la suite, ta gravitation constante 1D :

On part de la formule et le reste coule de source

Ex : Si l'accélération terrestre était constante à 10m/s² un objet lancé à 0,9c atteindrait 1,23AL en 1,96ans avant de faire demi-tour

Et ça va peut être t'aider à comprendre l'histoire du puzzle

A+
Mailou

[Zefram Cochrane]

Salut Mailou,
Je réponds à ce message
http://forums.futura-sciences.com/as...ml#post4735237

Je voudrais savoir à quoi correspond la courbe noire (du parallépipède mou je suppose) ?
As tu une idée de ce que pourrait représenter physiquement une surface d'espace-temps?


Pour la partie haute,
Est ce que le rapport des angles des deux objet est égale à 9?

Il est normal que tu aies une échelle de temps indentique pour Bleu que pour Rouge.

Le petit coté pratique de ce schéma est que la trajectoire de la lumière se présente comme une ligne horizontale. On a sur une même ligne horizontale, le temps propre, le temps coordonné et le temps apparent.

Cordialement,
Zefram

[Zefram Cochrane]

http://forums.futura-sciences.com/as...ml#post4735243

J'ai un peu du mal à intepréter ton schéma.
La figure de gauche est le cas avec une accélération constante, comme n l'avait vu précédemment. Mais je ne comprends pas celle de droite et à la mettre en relation avec ce que tu dis dans ton texte.

Cordialement,
Zefram

[Mailou75]

Salut,

Je voudrais savoir à quoi correspond la courbe noire (du parallélépipède mou je suppose) ?

Alors déjà ça serait plus un "parallélogramme mou", j'ai craqué...
Et la courbe noire c'est toujours la même : temps propre constant !
A gauche deux points sur la courbe auront le même âge (durée propre) depuis le départ
(ex: Quand Rouge a 18ans, Bleu, si il n'a pas fait demi tour, a lui aussi 18ans et se trouve à 24AL dans le futur (30ans) de Rouge, c'est leur distance comobile*)
A droite deux points sur la courbe auront la même durée propre avant l'arrivée
*[appellation très personnelle en RR mais correspondant à une définition connue : position des objets "au même âge"]

As tu une idée de ce que pourrait représenter physiquement une surface d'espace-temps?

En 4D les axes ont tous la même valeur!
Une surface (distance x temps.c) vaut bien une surface (distance x distance), celle d'une feuille de papier !
Il n'y a que les cosmologistes pour parler de l'évolution de l'espace dans le temps...

Est ce que le rapport des angles des deux objet est égale à 9?

Non, le rapport des distances angulaires vaut 9 : z+1 !
Mais Wiki te dira que si ton angle incident vaut alors ton angle vu sera tel que :
Mais attention dans le cas présent, entre les deux visions de Bleu, il faut prendre v=0,975c et le qui va avec
(Quoique je suis en train de me dire que la formule Wiki et peut être fausse... à voir)

Il est normal que tu aies une échelle de temps identique pour Bleu que pour Rouge.

Oui on le retrouve facilement mais je ne m'y attendais pas...
Cette représentation m'a l'air de flirter avec la version "RR trigo", je vais regarder ça de plus près

Le petit coté pratique de ce schéma est que la trajectoire de la lumière se présente comme une ligne horizontale. On a sur une même ligne horizontale, le temps propre, le temps coordonné et le temps apparent.

Temps propre de Bleu (6) dans les repères de Rouge
Temps coordonnée de Bleu (30) dans son repère
Temps apparent du "voyage de Bleu" (18) dans les repères de Rouge
Faut se méfier quand même...

........

La figure de gauche est le cas avec une accélération constante, comme on l'avait vu précédemment. Mais je ne comprends pas celle de droite et à la mettre en relation avec ce que tu dis dans ton texte.

Celle de droite c'est la construction : La courbe noire est celle d'une accélération à 10m/s²
D’après la formule on sait qu'à t=c/a un objet aura atteint la vitesse c
La portion de courbe comprise entre 0 et t sera donc répétée quatre fois en "symétries" pour un trajet aller retour "façon Vert"
Ensuite, comme tu le faisais remarquer, on peut transposer cette trajectoire et dire que l'accélération est toujours dirigée vers le même point et conserve une valeur constante quelle que soit la distance à ce point = gravitation 1D à accélération constante !

A+
Mailou

[Mailou75]

Re,

(Quoique je suis en train de me dire que la formule Wiki et peut être fausse... à voir)

Non non elle est juste. En fait ce que je raconte est juste aussi mais ponctuellement, pour le centre de l'objet.

Dès lors qu'il a une taille c'est plus pareil, deux facteurs entrent en jeu :
1. Il est compressé dans le sens du mouvement (rond > ovale)
2. Le diamètre perpendiculaire à la ligne de visée se tord (ovale > haricot)

Dans le dessin, l'erreur d'angle sur le 2 ne vaut même pas l'épaisseur de la ligne,
par contre le 1 est important à 0,8c mais il ne change rien aux lignes tracées.
Pour le 2 voir http://forums.futura-sciences.com/as...ml#post4628369 (pointillé rouge)

Donc c'est pas trop faux, mais je savais pourquoi je ne voulais pas m'étendre sur le sujet, c'est complexe...

A+
Mailou

[Zefram Cochrane]

Salut,

Temps propre de Bleu (6) dans les repères de Rouge
Temps coordonnée de Bleu (30) dans son repère
Temps apparent du "voyage de Bleu" (18) dans les repères de Rouge
Faut se méfier quand même...

Ne serait il pas intéressant de faire le même schéma pour Bleu tout compte fait?

Celle de droite c'est la construction : La courbe noire est celle d'une accélération à 10m/s²
D’après la formule on sait qu'à t=c/a un objet aura atteint la vitesse c
La portion de courbe comprise entre 0 et t sera donc répétée quatre fois en "symétries" pour un trajet aller retour "façon Vert"
Ensuite, comme tu le faisais remarquer, on peut transposer cette trajectoire et dire que l'accélération est toujours dirigée vers le même point et conserve une valeur constante quelle que soit la distance à ce point = gravitation 1D à accélération constante !

J'ai beau me faire des noeuds au cerveau, je ne comprends toujours pas la logique du diagramme de droite.
Je vois Vert accélérer à 10m/s pendant une période Tr puis accélérer dans l'autre sens pendant une période 2Tr et accélérer de nouveau dans le sens initial pendant une période Tr.


Prenons ton diagramme de gauche
Si j'ai compris ton calcul que je n'ai pas vérifié parce que je te fais confiance.
Si Vert s'éloigne de Rouge avec une vitesse initiale de 0,9c et qu'il accélère continuement de 10m/s² vers Rouge. Il atteindra une distance Hr de 1,23AL en Tr = 1,93ans avec une vitesse nulle.
Puis rejoindra Rouge au bout d'une durée d'environ en Tr =3,84 ans (2*1,93) avec une vitesse de 0,9c.

D'après le principe d'équivalence,
Vert génère un champs de gravitation uniforme de 10m/s²
Si Rouge décolle de Vert avec une vitesse initiale de 0,9c ( Rouge est en 'chute' libre dans le champ de gravitation; il est donc en acension libre pendant la première phase) il atteint la distance Hr de 1,23AL au bout de 1,93ans. Il retombera vers Vert qu'il atteindra à Tr = 3,84ans avec une vitesse de 0,9c.

Mon objectif à court terme est d'établir dans un premier temps les trajectoire de Vert dans le référentiel de Rouge (ce qui est déjà fait) et de Rouge dans celui de Vert. Puis, à moyen terme, d'établir leurs trajectoires apparentes.

Cordialement,
Zefram

[Mailou75]

Ne serait il pas intéressant de faire le même schéma pour Bleu tout compte fait?

Bof... je te le fais quand même



..............

J'ai beau me faire des nœuds au cerveau

C'est pourtant pas la peine, je t'ai peut être embrouillé avec mon Vert...
Il n'y a que Rouge et Bleu :
-A droite Bleu est immobile, Rouge part à v=0 et fait un aller-retour (comme tu le décris)
-A gauche Bleu est immobile, Rouge part à v=0,9c (ex) et fait le yoyo autour de Bleu (comme tu le décris)

Maintenant il faut trouver le moyen de faire varier a(d)
(GM/d² ou y'a plus "relativiste" ?)

Mon objectif à court terme est d'établir dans un premier temps les trajectoire de Vert dans le référentiel de Rouge (ce qui est déjà fait) et de Rouge dans celui de Vert. Puis, à moyen terme, d'établir leurs trajectoires apparentes.

"celui de Vert"? ça dépend de quel Vert tu parles, mais si il est accéléré tu ne pourras pas faire un Minkowski
(on a pu le faire pour Rouge qui n'empruntait que deux référentiels lors de son aller-retour)

[Mailou75]

Dès lors qu'il a une taille c'est plus pareil, deux facteurs entrent en jeu (...)

Pour Rouge au moment du demi tour Bleu passe d'une "banane rouge proche" à un "oeuf bleu éloigné"

En classique un objet "se trouvant" à un distance 1 (situé un un cercle de rayon 1) et se déplaçant à une vitesse v
sera vu projeté sur un cercle de même rayon décalé d'une distance v/c

En relativiste un objet "se trouvant"* à une distance 1 (situé un un cercle de rayon 1) et se déplaçant à une vitesse v
sera vu projeté sur une ellipse de demi petit axe 1 et de demi grand axe dont l'observateur est le foyer

En classique il n'y a pas compression de l'objet et il n'y a qu'une position "dans l'espace"
En relativiste l'opération s'effectue à partir de la position "comobile" (à âge égal depuis/avant rencontre) et non de la position dans l'espace
pourtant on peut vérifier que lorsqu'un rayon parcourt une distance D l'objet allant à 0,8c parcourt effectivement 0,8D dans l'espace...
Bref c'est pas encore très clair mais ça va venir

Le truc amusant dans tout ça c'est quand même que Rouge s'éloigne de Bleu
et qu'au moment où il décide de faire demi tour pour revenir vers Bleu, le premier truc qu'il verra c'est Bleu s'éloigner
(Est -ce là que tu voulais en venir ?)

A+
Mailou

[Mailou75]

Autre chose, si on trace le rayon de longueur L partant du même point mais de la positon comobile alors on aura :

D/L=z+1 ou d/L=z+1

Les z+1 ne vallant 3(red) et 0,33(bleu) que pour les points situés dans l'axe du déplacement

[Mailou75]

L/D=z+1 ou L/d=z+1 pardon...

[Zefram Cochrane]

Salut,
Pourrais tu décrire comment tu as fait pour établir ton dernier schéma STP?
J'ai bien compris ce que tu voulais dire pour Vn aller et retour. J'ai un peu plus de mal avec "comobile" et "espace", j'aimerai bien avoir quelques explication là dessus.
Cordialement,
Zefram