Je reprends (mieux ?) le cas d'une boule de poussière en chute radiale près d'une planète (solution de Schwarzschild): si on prend pour u la quadrivitesse du centre, sa partie spatiale est radiale ; pour n le 4-vecteur spatial séparant le centre et la poussière considérée, alors le résultat (un 4-vecteur) est la déviation du mouvement de cette poussière par rapport au mouvement du centre (la partie spatiale donne l'éloignement ou le rapprochement tant en direction qu'en module, et la partie temporelle le rythme de décalage temporel).
À vérifier.
-----



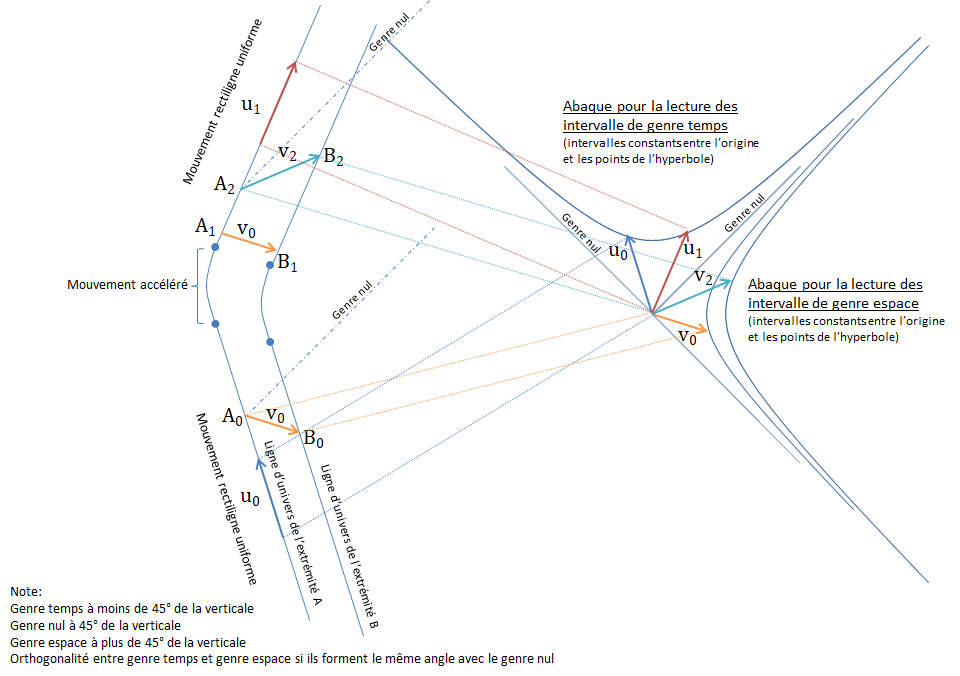
 , avec u, le vecteur tangent à l'une des deux géodésique, n, le vecteur "séparant" les deux géodésiques, le nabla symbolise la dérivée covariante. R(...,u,n,u) est le tenseur de Riemann, utilisé comme application linéaire transformant un triplet de vecteur en un unique vecteur (les pointillés, c'est parce qu'il y un "slot" inutilisé ici, dans lequel on peut insérer une forme linéaire).
, avec u, le vecteur tangent à l'une des deux géodésique, n, le vecteur "séparant" les deux géodésiques, le nabla symbolise la dérivée covariante. R(...,u,n,u) est le tenseur de Riemann, utilisé comme application linéaire transformant un triplet de vecteur en un unique vecteur (les pointillés, c'est parce qu'il y un "slot" inutilisé ici, dans lequel on peut insérer une forme linéaire).