Bonjour,
Bonjour,
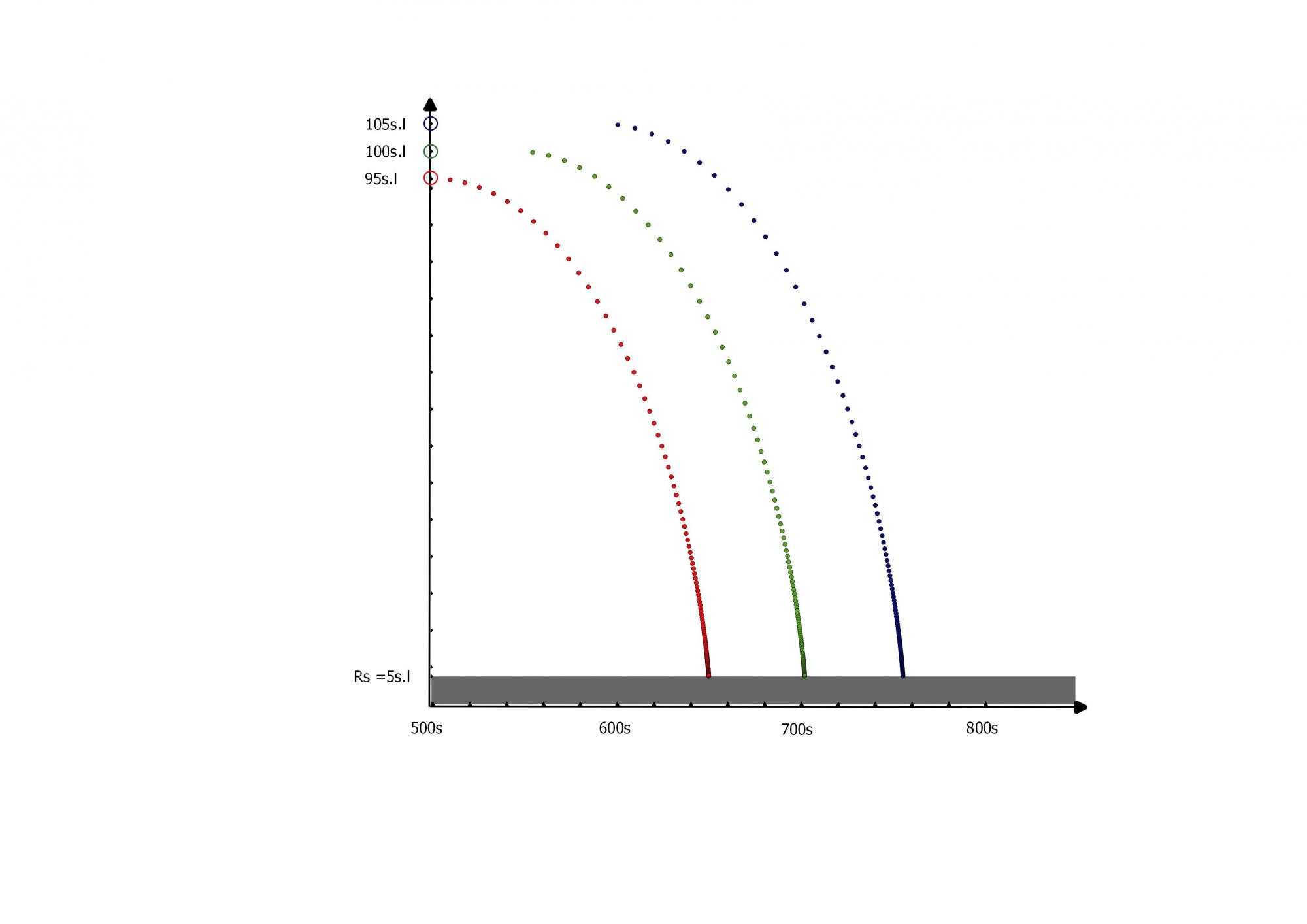
C'est ce qui disent les calculs :
une autre façon de voir est de considérer que la vitesse coordonnée de la lumière est [U]apparament[/B] nulle au niveau de l'horizon du TN (mais ce n'est qu'une apparence, cette nullité n'a rien de physique, mais explique pourquoi l'image de tout ce qui franchit l'horizon du TN apparait figé dans le temps.
Ce qu'on voit du TN est une étoile gelée.
De ce fait, théoriquement ce qu'on voit du TN est un empilement de sphères constituées d'images d'événements qui se seraient déposés en sédiments à la surface du TN.
Mais, il y a le fait que dès lors qu'un TN absorbe de l'énergie son rayon s'accroit. Car Rs = 2G(M + m)/c².
Ma question est donc est ce qu'en prenant du volume, cette représentation de sphères d'images sédimentées est rendue caduque?
-----




 de chute par rapport à la corde et la vitesse instantanée correspondante
de chute par rapport à la corde et la vitesse instantanée correspondante