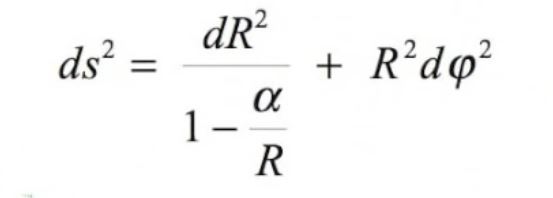Masse d'un trou noir

[mach3]

Lorsque, en raison 1, vous indiquez que la métrique en r (celle de Wikipédia) et celle en R (celle de Schwarzschild, que je vais appeler Karl pour gagner du temps de frappe) sont d’une expression simple, vous les réunissez de fait dans une seule qui serait retenue par la communauté.

La formule donnée sur le wiki français est :



La formule (14) dans l'article de Karl est :



C'est la même formule. C'est incontestable. la présence du c² dépend d'un choix de convention, la constante d'intégration alpha de Karl s'appelle maintenant rayon de Schwarzschild rs, et la graphie r remplace R.

Dans cette hypothèse, votre raison 2 devient un truisme, car la signification physique forte de R est la même que celle de r, chacun sachant depuis longtemps que la surface d’une sphère ne dépend pas de la graphie de son rayon !

on parle de quel "r" là? celui du papier de Karl? ou celui de la formule de wikipédia. Parce que dans le premier cas, non, "r" de Karl n'a pas la même signification que "R".

[...]Et cela va à l’encontre de votre affirmation initiale que « la coordonnée radiale » n’a pas de sens » parce qu’elle est imposée par la symétrie sphérique

ce n'est pas "coordonnée radiale" qui n'a pas de sens, c'est "La coordonnée radiale" qui n'a pas de sens, car il en existe une infinité. Le point est que parmi ces coordonnées radiales, il en est une qui a un sens précis, une "signification physique forte" que n'ont pas les autres coordonnées radiales possibles, et c'est "R" dans la l'article de Karl (qui est "r" dans le wiki).

Deux lignes sont utiles pour apprécier la différence entre r et R:
la première, celle de la définition de r, qu’il présente en coordonnées cartésiennes, mais simplement pour constater qu’elle est celle d’un rayon identifiable au r précédent en coordonnées polaires.

Ensuite la lecture de la métrique elle même

A côté de la formule, que vous jugez à juste titre d’expression simple, et après la virgule, il y a la relation entre r et R qui les distingue définitivement, et dont vous ne pipez mot.

Je ne sais pas pour amanuensis, mais moi là j'ai juste l'impression d'être pris pour un idiot. Va falloir éviter ça à l'avenir si vous souhaitez que la discussion se poursuive sereinement.

Et c’est là toute la différence avec la métrique précédente en r :
Quand r est plus petit que alpha, R devient négatif.
Ce n’est d’ailleurs pas grave pour Karl, car quand r = r_s, on est sur le bord intérieur de l’espace, et la symétrie sphérique est conservée. Simplement il n’y a plus d’espace à l’intérieur pour r.
On a deux solutions vraiment différentes, pour le même problème.
On ne peut aller plus loin sans démontrer laquelle est la bonne.

Non, c'est quand r est plus petit -alpha que R devient négatif... R plus petit que alpha fait que r est négatif en revanche.
Comparer r et rs n'a pas trop de sens, étant donné que rs est une valeur de "R", pas de "r". Quand R vaut rs, r vaut 0.

Non, on n'a pas deux solutions différentes. C'est une seule et unique solution.

m@ch3
-----

[Mailou75]

Salut,

La formule donnée sur le wiki français est :



La formule (14) dans l'article de Karl est :



C'est la même formule. C'est incontestable.

Je me trompe sans doute mais je ne suis pas d'accord.

Admettons par principe que devienne . Le changement de vers n'est pas gratuit : si c'était un simple changement de variable tel que (je mets prime pour le différencier de l'autre , celui ci n'apparait pas dans les formules citées) alors tu aurais raison, ce serait exactement pareil. Comme tu le dis, on vérifie que pour on a mais c'est un cas particulier.

Pour ce que j'en comprend la différence réside dans une variation de volume et est différent de . Ceci veut dire que le volume du trou noir, défini par et constant, augmenté d'une valeur est différent du même volume additionné à un autre petit volume de rayon . Karl (bonne idée ce raccourci lol) semble se servir de volumes pour définir des distances, le volume du trou noir est centré sur un point mais le volume de rayon est abstrait et ne sert qu'à définir , justement. Du coup, dans la formule actuelle : est en mètres et dans la formule "14" (+ relation entre les "r") : est en mètres, est en mètres mais le injecté dans la formule n'est plus en mètres mais en "mètres + r_s".

En même temps je lis très mal dans les formules donc je suis potentiellement en plein hors sujet. Vous m'en excuserez si c'est le cas.

Mailou

[mach3]

Admettons par principe que devienne .

En dérivant sa solution, Schwarzschild fait apparaitre différentes constantes (suite à des intégrations), constantes dont il faut chercher la valeur par la suite. Dans le papier de Schwarzschild, le travail est "inachevé" car il reste la constante alpha dont la valeur n'est pas fixé (toutes les autres ont disparu). La suite de la "manoeuvre", qui n'est pas dans ce papier, c'est de regarder les géodésiques "au loin" (pour des grandes valeurs de R), et les comparer avec les trajectoires Kepleriennes autour d'un astre de masse M. On trouve alors que alpha vaut 2GM/c². Cette quantité a ensuite été nommée rayon de Schwarzschild en l'honneur de celui-ci (mais, comme souvent pour les termes scientifiques, le terme est mal choisi, car 2GM/c² n'est pas un rayon...). Note pour rappel, on ne choisi pas la masse au départ, vu qu'on envisage une solution du vide, il se trouve qu'on obtient une solution du vide avec un paramètre libre (alpha) et que la comparaison avec la physique classique permet d'associer une masse avec alpha.

Je ne comprend pas le reste, notamment "le changement de r vers R n'est pas gratuit". De quel r parle-t-on? r est-il celui qui figure dans le papier de Schwarzschild? ou celui qui figure dans ?
Dans le deuxième cas, c'est juste une substitution d'une lettre par une autre (r de wikipedia = R du papier de Schwarzschild).

Dans le premier cas, il faut réécrire la métrique pour passer de R à r, et ça donne, comme déjà dit :



et ça soufre des mêmes "travers" que l'expression en fonction de R : singularité de coordonnée si on ne spécifie pas bien le domaine de définition de r, changement de genre possible pour t et r.

m@ch3

[Amanuensis]

Il me semble que votre lecture sur Wikipédia n’a pas été suffisamment attentive (comme d’ailleurs celle de mach 3)

Ce genre de remarque est largement suffisant pour moi pour cesser tout échange.

[Amanuensis]

alors dans ce cas, ce ne doit pas être ce champs scalaire "r" (*) qu'il faut considérer, car ce "r" là nous amène dans la région II quand il est négatif (si r<0, r est de genre temps et t de genre espace).

Uniquement si on veut garder la métrique tel quel. Comme je l'ai écrit il me semble, en notant r' la coordonnée notée r par Schw, la transformation (t, r') -> (t, -r') n'est pas pas une isométrie en conservant la métrique tel quel. Mais cela n'interdit pas qu'il existe une isométrie entre I et III ; ce d'autant moins qu'on en connaît une! À savoir celle qu'on construit trivialement avec les coordonnées de KrSz (entre les régions (X>0, X²>T²) et (X<0, X²>T²)).

Et, si on prend l'espace-temps de Kruskal, ces deux parties isométriques sont reliées continument par la sphère X=T=0.

Un champ scalaire de type , avec en plus une transformation qui amène rs et -rs sur 0 conviendrait mieux pour passer de I à III non?

Je ne comprends pas. Pourquoi pas le champ scalaire X? Et prendre un champ non défini en X=0 ruine l'idée d'un passage continu entre I et III, non?

----

Je suis bien d'accord que travailler avec r' (le r de Karl) ne permet pas de «supprimer» la région II (en fait II et IV) ; mais ce n'est pas parce que r' est un mauvais outil qu'il n'y en pas d'autres permettant de le faire.

[Amanuensis]

PS: Soyons clair: je ne défends pas l'idée (a priori fausse) qu'on puisse compléter la solution du vide dans la région I par une solution du vide sans région II. Je m'intéresse juste à que ce soit démontré proprement. Qu'on échoue à le faire avec la coordonnée r' et une assimilation (t, -r')=(t,r') n'est pas suffisant.

Le point critique est l'extension des lignes d'univers tendant (en coordonnées de Schw.) vers (infini, r_s), qui existent avec un temps propre borné et une qvitesse tendant vers une valeur définie (autre manière de dire que la forme métrique reste définie). L'existence de telles lignes «sans extension» n'a de sens physique que si on les étend.

Or ce n'est pas discuté dans ces «échanges», le focus étant seulement sur la ligne r=r_s, t fini. Ce qui «évite» de considérer les bonnes démonstrations.

(Opinion personnelle: je soupçonne que l'incapacité à accepter une prolongation d'une ligne «après» l'infini de t vient d'une conceptualisation bloquée sur l'idée de temps absolu. Il y a un pas difficile à passer pour accepter que ce "t" qui rend la solution statique ne soit qu'une coordonnée qu'un changement de coordonnée montre comme «dépassable». Surtout qu'elle est bien indépassable pour les lignes d'univers restant avec r>r_s+ε, ε strictement positif.)

[Amanuensis]

PPS: Le «conflit» est entre considérer les lignes d'univers tendant vers (infini, r_s) comme sans sens physique soit a) parce que la physique exige leur extension, b) parce qu'il serait aberrant de prolonger au-delà de t infini.

Accepter qu'il n'est pas aberrant de prolonger au-delà de t infini demande d'avoir intégrer correctement la philosophie du temps de la RG. Et il est patent que ce n'est pas aisé.

Or c'est cette acceptation (l'option a)) qui amène à construire la région II...

[mach3]

Uniquement si on veut garder la métrique tel quel. Comme je l'ai écrit il me semble, en notant r' la coordonnée notée r par Schw, la transformation (t, r') -> (t, -r') n'est pas pas une isométrie en conservant la métrique tel quel. Mais cela n'interdit pas qu'il existe une isométrie entre I et III ; ce d'autant moins qu'on en connaît une! À savoir celle qu'on construit trivialement avec les coordonnées de KrSz (entre les régions (X>0, X²>T²) et (X<0, X²>T²)).

C'est subjectif et arbitraire, mais je préfère que l'écriture de la métrique ne dépende pas de la région et que les champs scalaires utilisés comme coordonnées soit définis de façon à ce que ce soit le cas. Après on est libre de définir les champs scalaires de manière à ce que la métrique s'écrive différemment selon la région, je suis bien d'accord, c'est donc avant tout une histoire de goût (c'est comme l'histoire d'avoir le champ scalaire t croissant ou décroissant dans le sens passé->futur dans la région III, histoire de goût).

Je ne comprends pas. Pourquoi pas le champ scalaire X? Et prendre un champ non défini en X=0 ruine l'idée d'un passage continu entre I et III, non?

mon but était d'avoir un champ scalaire qui vaut R quand X>0 et -R quand X<0, donc j'ai bricolé ce truc, mais je me suis pris les pieds dans le tapis, j'ai pas réfléchi que mon expression faisait que c'était indéfini en X=0. Disons alors plutôt , comme ça ça fonctionne.
(en fait je ne voulais pas faire apparaitre la fonction signe, pour des raisons de "gout", du coup je l'avais remplacé par X/|X| qui fait comme la fonction signe, sauf que non définie en X=0, ce à quoi je n'ai pas fait attention, et en touillant un peu ça a donné l'expression de mon message précédent).
Il faut aller un chouillat plus loin pour avoir un champ scalaire, disons r', allez, qui vaut r quand X>0, -r quand X<0 et 0 quand X=0 (pas pris le temps de faire), et si on utilise ce champ scalaire r' comme coordonnée radiale, alors les coefficients de la métrique seront les mêmes en (t,r') et (t,-r') et on peut imaginer un passage continu de I à III. Après la question se pose du sens de t dans la région III pour que ce passage soit "joli" (pas encore assez réflechi, mais l'idée est que ce passage doit avoir la même tête pour toute valeur de t, et j'intuite qu'il faut pour cela que t soit décroissant dans le sens passé-futur en région III).

Je suis d'accord sur les PS. Le souci est que notre interlocuteur semble éluder le problème de l'extensibilité des géodésiques.

m@ch3

[Amanuensis]

Le plus direct est de prendre r = sgn(X) r_s(1+W0((X²-T²)/e)), et de changer r en |r| là où il faut.

Car on garde alors le fait que l'aire de la sphère spatiale est 4πr².

(Par ailleurs on peut justifier le changement de signe en prenant la normale à la surface, puisque relativement à la sphère X=T=0, I est d'un côté et III de l'autre.)

[Amanuensis]

Corrigendum: Message précédent n'importe quoi, désolé.

Lire: Le plus direct est de prendre ρ = sgn(X) r_s(W0((X²-T²)/e)), et de changer r en r_s+|ρ| là où il faut.

L'aire de la sphère spatiale est 4π(r_s+|ρ|)².

(Par ailleurs on peut justifier le changement de signe en prenant la normale à la surface, puisque relativement à la sphère X=T=0, I est d'un côté et III de l'autre.)

[bernarddo]

En dérivant sa solution, Schwarzschild fait apparaitre différentes constantes (suite à des intégrations), constantes dont il faut chercher la valeur par la suite. Dans le papier de Schwarzschild, le travail est "inachevé" car il reste la constante alpha dont la valeur n'est pas fixé (toutes les autres ont disparu). La suite de la "manoeuvre", qui n'est pas dans ce papier, c'est de regarder les géodésiques "au loin" (pour des grandes valeurs de R), et les comparer avec les trajectoires Kepleriennes autour d'un astre de masse M. On trouve alors que alpha vaut 2GM/c². Cette quantité a ensuite été nommée rayon de Schwarzschild en l'honneur de celui-ci (mais, comme souvent pour les termes scientifiques, le terme est mal choisi, car 2GM/c² n'est pas un rayon...). Note pour rappel, on ne choisi pas la masse au départ, vu qu'on envisage une solution du vide, il se trouve qu'on obtient une solution du vide avec un paramètre libre (alpha) et que la comparaison avec la physique classique permet d'associer une masse avec alpha.

Je ne comprend pas le reste, notamment "le changement de r vers R n'est pas gratuit". De quel r parle-t-on? r est-il celui qui figure dans le papier de Schwarzschild? ou celui qui figure dans ?
Dans le deuxième cas, c'est juste une substitution d'une lettre par une autre (r de wikipedia = R du papier de Schwarzschild).

Dans le premier cas, il faut réécrire la métrique pour passer de R à r, et ça donne, comme déjà dit :



et ça soufre des mêmes "travers" que l'expression en fonction de R : singularité de coordonnée si on ne spécifie pas bien le domaine de définition de r, changement de genre possible pour t et r.

m@ch3

Ok quand à la définition de alpha.
Mais le terme de rayon de Sch n'est pal mal choisi, il a la dimension d'une longueur en mécanique relativiste.

Pour le reste je partage l'objection de Mailou75

La solution 2 est simplement la position de la communauté, qui justifie (faussement) qu'il y aurait identité entre les formules Wiki et Karl.

On n'a pas le droit de le faire, car le sens mathématique du r de Wiki (rayon en coordonnées polaires) est le même que celui du r de Karl (même rayon qu'il définit en coordonnées cartésiennes (*).avant de faire son calcul en polaires.
si r wiki = r karl, alors la formule de Karl, exprimée en coordonnées polaires R4, est celle de la solution 1 différente de la formule wiki.

Les trajectoires (non interrompues) s'inscrivent alors dans des hypersurfaces qui ne sont que des extensions du type de celles existant sur le diabolo que j'ai présenté en post #59, intrinsèquement continues et qui ne s'interrompent que si on veut les plonger dans un référentiel R2

(*)[r = racine (dx2 +dy2+dz2)], comme montré en #90, post dans lequel je me suis mélangé les pinceaux quand j'ai écrit "Quand r est plus petit que alpha, R devient négatif" ,comme l'a bien noté mach3.

[bernarddo]

Ce genre de remarque est largement suffisant pour moi pour cesser tout échange.

Je comprends qu’avoir considéré une de vos lectures comme peu attentive ait pu vous chagriner, mais il me semble que ce n’est que peu de choses en rapport aux sarcasmes dont j’ai été abreuvé, (c’est votre propre ressenti du # 78), et je n’en ai pas pour autant mis fin à une discussion qui me semblait nous enrichir mutuellement.
D’autre part, je n’ai jamais prétendu être capable de maîtriser toutes les mathématiques de façon suffisamment exhaustive pour fournir toutes les réponses claires au souhait que vous émettez dans le même post, ou même eté incapable d’exprimer correctement ma pensée ce qui peut conduire à des incompréhensions.
Je compte bien participer tant que des contributeurs voudront bien s’intéresser à mes posts et espère pouvoir vous compter encore parmi eux.

[mach3]

Ok quand à la définition de alpha.
Mais le terme de rayon de Sch n'est pal mal choisi, il a la dimension d'une longueur en mécanique relativiste.

Pour le reste je partage l'objection de Mailou75

La solution 2 est simplement la position de la communauté, qui justifie (faussement) qu'il y aurait identité entre les formules Wiki et Karl.

On n'a pas le droit de le faire, car le sens mathématique du r de Wiki (rayon en coordonnées polaires) est le même que celui du r de Karl (même rayon qu'il définit en coordonnées cartésiennes (*).avant de faire son calcul en polaires.
si r wiki = r karl, alors la formule de Karl, exprimée en coordonnées polaires R4, est celle de la solution 1 différente de la formule wiki.

Les trajectoires (non interrompues) s'inscrivent alors dans des hypersurfaces qui ne sont que des extensions du type de celles existant sur le diabolo que j'ai présenté en post #59, intrinsèquement continues et qui ne s'interrompent que si on veut les plonger dans un référentiel R2

(*)[r = racine (dx2 +dy2+dz2)], comme montré en #90, post dans lequel je me suis mélangé les pinceaux quand j'ai écrit "Quand r est plus petit que alpha, R devient négatif" ,comme l'a bien noté mach3.

le r de wiki n'est pas le r de Karl, mais le R de karl. Le r de wiki est tel que l'ensemble d'évènement de même coordonnées r et t est une sphère de surface . Le R de Karl c'est pareil. C'est pas moi qui le dit c'est les maths.

En géométrie euclidienne, dans un système de coordonnées cartésiennes (x,y,z) on peut définir un champ scalaire r tel que r²=x²+y²+z². Il est tel que l'ensemble des points de même r forment une sphère de rayon r et d'aire . En géométrie non euclidienne, dans le cas particulier d'une variété avec symétrie sphérique qui est Euclidienne loin du centre, une sphère centré de rayon r' (*) n'aura pas une aire de : la courbure modifie la relation entre l'aire d'une sphère et le rayon de cette sphère.
Ainsi, si on considère sur cette variété, un système de coordonnée tel que la métrique tend vers celle d'Euclide très loin du centre (ds²-->dx²+dy²+dz² pour x²+y²+z²-->infini), on peut tout à fait définir un champ scalaire r tel que r²=x²+y²+z², mais il ne sera pas tel que l'ensemble des points de même r forment une sphère d'aire . C'est un autre champ scalaire, R, qui sera tel que l'ensemble des points de même R forment une sphère d'aire . Les deux champs r et R ne sont identiques que dans le cas particulier d'un espace euclidien plat.

*: quand celui-ci est définissable...

m@ch3

[invite6486d7bd]

Petite digression.

Ce qui me gène ici dans la représentation des phénomènes physiques c'est qu'il y est question d'un espace absolue que l'on cherche à tordre pour rendre compte au mieux de la réalité observationnelle, qui cesse d'être "euclidienne" lorsque les "distances" (on peut aussi dire le temps lumière pour se rendre à un emplacement du phénomène) augmentent.

Le problème de base, à mon sens, vient de la vue de l'esprit, représentation naïve que nous nous faisons de notre environnement, et certes utile dans un environnement commun (celui des animaux sur Terre par exemple), mais qui est fausse d'un point de vue physique.

Par exemple, si je reprends l'exemple de la carte terrestre proposée plus avant, cette carte et même la sphère que l'on conçoit aussi bien mathématiquement que par l'esprit, comme "placée" dans un espace tridimensionnel extérieur au phénomènes, ne sont pas valables physiquement.
physiquement, ça veut dire "au plus proche du phénomène", or il n'est pas possible de représenter l'ensemble des phénomènes locaux dans un espace global (qui serait par exemple tridimensionnel).

Sans rentrer dans le détail de toutes les implications, il me semble qu'on peut pourtant employer une représentation plus proche de la réalité physique.

Premièrement, il n'est pas question de mélanger les types d'observateurs, puisque la "carte" dépend de la nature de l'observateur. Il faut donc définir la nature de "l'objet" auquel la carte est associée.
D'autre part, il faut également s'attacher à ne pas mélanger les types d'interaction auquel l'observateur est soumis.
Par exemple, dans le cas de la carte terrestre, un observateur éloigné ne subirait pas les effets des liaisons atomiques et il est ici question de lumière et de gravité (même si on imagine, dans notre esprit qu'il existe bien de la matière depuis laquelle la lumière ou la gravité se fait ressentir).
Reste donc à définir la "position" d'émission de la lumière, par exemple, en relation avec l'orientation de l'observateur.
Soit un angle gauche/droite, un angle haut/bas, une "distance" (qui peut être un temps pour la lumière).
Ce qui est intéressant, à mon sens dans cette représentation "3D", parfaitement physique (du moins c'est ce qui m'apparait), c'est que les objets situés à la même "distance", se situent naturellement dans un arc de cercle ... soit sur un plan.
Il est d'ailleurs amusant et instructif de visualiser la représentation physique des emplacements de la sphère terrestre selon cette "déformation" (qui physiquement n'en est pas une ...) relativement à l'idée naïve que nous nous faisons de la sphère terrestre plongée dans un espace tridimensionnel.
On notera également qu'il existe de multiples "cartes" possibles, selon la nature de l'observateur ainsi que le type d'interaction.

[Mailou75]

Salut,

Pour le reste je partage l'objection de Mailou75

Ca fait plaisir à entendre ! Comme je ne suis pas sur d'avoir été très clair j'ai fait un petit dessin montrant ce à quoi je pensais.

Le trou noir a un rayon Rs=3m et la variable de distance extérieure est r'=2m (quantités et unités au pif)
Le volume du trou noir est 27m³ et le volume d'une sphère de rayon r' et 8m³
(on oublie les qui ne changent rien au problème, pour la clarté)

A gauche Wiki nous dit que la coordonnée r = Rs + r' =5m soit une sphère de volume 125m³

A droite Karl nous dit que la coordonnée R = 3,271m car 3,271³=35m³=27+8 ce qui respecte la définition de R :
Le volume jaune de rayon r' est le même que la coque située entre le trou noir et la sphère rouge de rayon R (voir flèche)

Est-juste pour définir la différence entre les deux formules ?

Merci

Mailou

[mach3]

@mailou, juste lu en diagonal, mais ça ne tient pas debout. On ne peut pas utiliser le volume dans sa définition euclidienne dans une variété qui n'est pas euclidienne.

m@ch3

[Amanuensis]

Ce qui me gène ici dans la représentation des phénomènes physiques c'est qu'il y est question d'un espace absolue que l'on cherche à tordre pour rendre compte au mieux de la réalité observationnelle

Non.

Déjà, même en classique il n'y a pas d'espace absolu.

Ensuite ce qui est «tordu» est l'espace-temps.

Ensuite, ce qu'on cherche à rendre compte sont les mouvements (c'est ça, l'espace-temps: de quoi modéliser les mouvements), et ce en incluant la gravitation et l'inertie.

Ensuite, la notion d'espace (déjà pas absolue en classique) est relativisé complètement.

, qui cesse d'être "euclidienne"

Cela ne sert pas à grand chose de raisonner en termes d'espace qui serait euclidien ou pas. Seuls les raisonnements sur l'espace-temps amènent à quelque chose.

lorsque les "distances" (on peut aussi dire le temps lumière pour se rendre à un emplacement du phénomène) augmentent.

Pas seulement les distances, mais les durées, et les relations entre distances et durées.

Le problème de base, à mon sens, vient de la vue de l'esprit, représentation naïve que nous nous faisons de notre environnement, et certes utile dans un environnement commun (celui des animaux sur Terre par exemple), mais qui est fausse d'un point de vue physique.

Ce n'est en rien un problème à notre échelle, au contraire. Cela ne le devient que si on se bloque dessus pour essayer de comprendre la RG. Et le problème de fond n'est pas l'espace (qui, répétition, est déjà relatif en mécanique classique) mais le temps.

Par exemple, si je reprends l'exemple de la carte terrestre proposée plus avant, cette carte et même la sphère que l'on conçoit aussi bien mathématiquement que par l'esprit, comme "placée" dans un espace tridimensionnel extérieur au phénomènes, ne sont pas valables physiquement.

?? La carte proposée est des maths, comment représenter la surface d'une sphère sur un plan. En quoi un raisonnement sur la validité physique peut-il avoir un effet sur les bêtes maths de la cartographie?

physiquement, ça veut dire "au plus proche du phénomène", or il n'est pas possible de représenter l'ensemble des phénomènes locaux dans un espace global (qui serait par exemple tridimensionnel).

Pas dans un espace tridi, mais dans un espace-temps 4D. Il n'y a pas beaucoup de phénomènes sans mouvement! Et la mécanique classique est déjà une représentation en 4D, même si c'est caché dans des fonctions dépendant du temps.

Sans rentrer dans le détail de toutes les implications, il me semble qu'on peut pourtant employer une représentation plus proche de la réalité physique.

Ce serait intéressant au contraire d'avoir les détails, et surtout sous forme de modèle mathématique. Seul moyen de sortir d'un bla-bla littéraire laissant place à tout et n'importe quoi.

Premièrement, il n'est pas question de mélanger les types d'observateurs, puisque la "carte" dépend de la nature de l'observateur.

Absolument pas. Une carte est juste un outil de description. N'importe quel observateur peut adopter n'importe quelle carte.

Il faut donc définir la nature de "l'objet" auquel la carte est associée.

À développer pour que ce soit compréhensible, et pas par du bla-bla. Des maths. Une carte, c'est du domaine des maths.

D'autre part, il faut également s'attacher à ne pas mélanger les types d'interaction auquel l'observateur est soumis.

De plus en plus bla-bla.

Par exemple, dans le cas de la carte terrestre, un observateur éloigné ne subirait pas les effets des liaisons atomiques et il est ici question de lumière et de gravité (même si on imagine, dans notre esprit qu'il existe bien de la matière depuis laquelle la lumière ou la gravité se fait ressentir).

Et avec de moins en moins de sens perceptible.

J'arrête, ça empire après.

[Amanuensis]

@mailou, juste lu en diagonal, mais ça ne tient pas debout. On ne peut pas utiliser le volume dans sa définition euclidienne dans une variété qui n'est pas euclidienne.

De même qu'on ne peut pas utiliser les formules euclidienne d'aire pour les surfaces sur une sphère.

Cela semble quand même évident que l'aire de la surface délimitée par la ligne définie par une même distance r d'un point n'est pas πr² sur une sphère.

Quelques jolis dessins en géométrie 3D de base permet aisément de le montrer. Une bonne base avant de sauter directement à la chronogéométrie 4D courbe et aux «trous noirs».

[Mailou75]

@mailou, juste lu en diagonal, mais ça ne tient pas debout. On ne peut pas utiliser le volume dans sa définition euclidienne dans une variété qui n'est pas euclidienne.

Ok, j’me disais aussi... trop simple

Merci

[bernarddo]

C'est finalement une bonne illustration de la démonstration de Karl, puisque quand r' tend vers 0, le volume de la "coque" tend vers vers 0, et cela donne une image très parlante du fait que rs est un "bord" de l'espace-temps et qu'il n'y a rien à l'intérieur (volume nul)

[bernarddo]

Salut,



Ca fait plaisir à entendre ! Comme je ne suis pas sur d'avoir été très clair j'ai fait un petit dessin montrant ce à quoi je pensais.

Le trou noir a un rayon Rs=3m et la variable de distance extérieure est r'=2m (quantités et unités au pif)
Le volume du trou noir est 27m³ et le volume d'une sphère de rayon r' et 8m³
(on oublie les qui ne changent rien au problème, pour la clarté)

A gauche Wiki nous dit que la coordonnée r = Rs + r' =5m soit une sphère de volume 125m³

A droite Karl nous dit que la coordonnée R = 3,271m car 3,271³=35m³=27+8 ce qui respecte la définition de R :
Le volume jaune de rayon r' est le même que la coque située entre le trou noir et la sphère rouge de rayon R (voir flèche)

Est-juste pour définir la différence entre les deux formules ?

Merci

Mailou

C'est finalement une bonne illustration de la démonstration de Karl,
Celui-ci nous dit que l'espace-temps est continu, et son calcul le conduit à considérer que l'intérieur de la sphère r = r_s est hors de l'espace-temps intrinsèque.
Le volume de la coque est le volume d'espace(-temps) qui subsiste quand on est éloigné de r'.
Le calcul montre bien que, quand r' tend vers 0, le volume de la "coque" tend vers vers 0, et que si on prolonge le calcul Wiki pour des r inférieurs à r_s, r' devient négatif et ce volume de coque n'a plus de sens physique dans les coordonnée Wiki. Il faut alors considérer, comme Karl, qu'on n'est alors plus dans l'espace-temps (alors que R reste défini).

[mach3]

Non. C'est simplement que si on considère seulement R>rs (ou r>0) on ne cartographie pas tout l'espace-temps : il y a un trou dans la carte. Ca ne veut pas dire qu'il y a un trou dans le territoire. Qu'il y ait un trou dans la carte ne démontre rien, sinon qu'il y a des chances que la carte soit mal fichue. Si on souhaite montrer qu'il y a un trou dans le territoire, ce n'est pas à la carte trouée qu'on doit s’intéresser, où alors il faut pouvoir montrer qu'il n'existe aucune carte sans trou...

m@ch3

[Amanuensis]

Si on souhaite montrer qu'il y a un trou dans le territoire, ce n'est pas à la carte trouée qu'on doit s’intéresser, où alors il faut pouvoir montrer qu'il n'existe aucune carte sans trou...

Aucun atlas sans trou...

L'extensibilité intervient pour distinguer les «cartes trouées» et un atlas complet. Soit C une carte (ouverte). Si on peut produire une deuxième carte (ouverte) C' non incluse dans C mais avec une partie C' isométrique à une partie de C, la combinaison des deux décrit une variété plus grande que C seule : c'est une extension. De proche en proche, on peut construire un atlas non extensible, complet.

Par exemple une carte de S2 a nécessairement au moins un trou (Mercator en a deux.) En rajoutant une carte couvrant le trou (typiquement un pôle!) avec isométrie partielle avec la première, on obtient un atlas de S2, sans trou.

[mach3]

Tiens, il y a une traduction du papier de Karl sur arXiv : https://arxiv.org/abs/physics/9905030

Les traducteurs semblent être des "amis" de Bernarddo :

Translation by S. Antoci and A. Loinger of the fundamental memoir, that contains the ORIGINAL form of the solution of Schwarzschild's problem. The solution is regular in the whole space-time, with the only exception of the origin of the spatial co-ordinates; consequently, it leaves no room for the science fiction of the black holes. (In the centuries of the decline of the Roman Empire people said: ``Graecum est, non legitur''...).

j'espère que la traduction n'est pas "orientée"...

m@ch3

[Amanuensis]

(...)

(J'ai présenté cela avec des isométries à cause du contexte: en RG on s'intéresse à des variétés munies d'une forme «métrique». Les notions de carte et d'atlas sont plus généralement topologiques, et la relation entre cartes est un homéomorphisme pas une isométrie. Une isométrie est un difféomorphisme qui conserve la forme métrique, et un difféomorphisme est un homéomorphisme respectant la structure différentielle.

Le domaine des mathématiques couvrant cela est celui des variétés (manyfolds en anglais).)

[Amanuensis]

Tiens, il y a une traduction du papier de Karl sur arXiv : https://arxiv.org/abs/physics/9905030

Cette traduction était déjà citée par Bernarddo...

Les traducteurs semblent être des "amis" de Bernarddo :

Je l'avais déjà noté. Je ne pense pas que la traduction soit orientée. Par contre c'est «l'orientation» des traducteurs qui les amené à entreprendre cette traduction, qui n'a au fond qu'un intérêt historique. Y référer autrement que pour l'histoire est juste un moyen «d'argumenter» dans le mode philosophique (analyse de textes d'auteurs présentés comme *«de référence», étude de leur «pensée», ...), sur des sujets que les gens rationnels argumentent dans le mode mathématique.

Le point est que Schwarzschild découvrait la solution et l'a présentée avec les interprétations et les biais de son époque, et qu'il a fallu, comme souvent en physique, des années pour sortir l'idée de sa gangue d'origine, gangue due à la manière ancienne de pensée, manière que d'ailleurs la solution de Schw. et d'autres ont contribuer à rendre obsolète.

Si on s'intéresse à l'idée en elle-même et non à son histoire, on se fiche de ces textes originaux, les présentations plus modernes étant bien meilleures conceptuellement, tant du point de vue mathématique que physique, résultat de dizaines d'années de réflexion scientifique sur ces concepts.

[bernarddo]

L'extensibilité intervient pour distinguer les «cartes trouées» et un atlas complet.

A moins qu'elle ne vienne pour cartographier le diabolo dont on parlait plus haut, pour lui donner une image dans tout R3. (ce n'est évidemment qu'une analogie, mais plus facile à comprendre).

Le diabolo est "troué", (en topologie on dit qu'il n'est pas contractile), et donc il admet parfaitement une carte trouée (la projection de sa description par exemple) et une dimension en Z.
On peut le représenter sur un atlas complet, mais si celui-ci est "troué" au bon endroit (que j'appellerai au hasard zone d'extension,), on ne perdra aucune information, et surtout on évitera de le chercher dans la zone du trou.


A ce propos, sa métrique peut être écrite:

[Mailou75]

Salut,

Je ne comprends pas la moitié des réponses qui me sont faites et le sujet me depasse (je dois faire un blocage sur le terme metrique). Si le sujet me semblait interessant j’avoue ne même pas en saisir les enjeux, vos discours etant parsemés ne notions mathématiques occultant le fond du problème géométrique. Aussi, je m’en excuse auprès de Bernarddo mais je vais me ranger du coté d’Amanuensis et supposer qu’un paquet de physiciens se sont penchés sur le sujet et sont arrivés à la formule actuelle. Peut être ont ils raté une etape que Karl avait comprise, ce n’est pas impossible puisqu’il existe d’autres domaines où malgré 100 ans d’etude on reste à la ramasse... sur ce je retourne tenter de resoudre mes propres questions.

A+ bon courage. S’il en ressort qu’on doit revoir tous les systèmes de coordonnées tenez nous au jus

[mach3]

A moins qu'elle ne vienne pour cartographier le diabolo dont on parlait plus haut, pour lui donner une image dans tout R3. (ce n'est évidemment qu'une analogie, mais plus facile à comprendre).

Le diabolo est "troué", (en topologie on dit qu'il n'est pas contractile), et donc il admet parfaitement une carte trouée (la projection de sa description par exemple) et une dimension en Z.
On peut le représenter sur un atlas complet, mais si celui-ci est "troué" au bon endroit (que j'appellerai au hasard zone d'extension,), on ne perdra aucune information, et surtout on évitera de le chercher dans la zone du trou.


A ce propos, sa métrique peut être écrite:
Pièce jointe 378371

c'est connu. C'est une métrique de la paraboloïde de Flamm, qui est décrite par dans l'espace euclidien avec des coordonnées cartésiennes.

Il suffit de faire le changement de variable suivant : , , , et quelques différenciations pour obtenir la métrique.

Mais ça ne couvre qu'une moitié du diabolo, et exclut le cercle "central" de rayon alpha. Il faut faire disparaitre R au profit de z dans la métrique pour qu'elle couvre tout le diabolo, ou, comme c'est fait plus couramment, introduire u, tel que , ce qui donnera la métrique suivante :



Qui est parfaitement définie pour tout réel u, y compris 0 qui correspond à R=alpha.

Effectuons le même changement de variable sur la métrique de Schwarzschild :



devient :


La singularité de coordonnée disparait (vu de Kruskal-Szekeres, on couvre les régions I et III, c'est ce qu'on appelle le pont de Rosen, ou encore le trou de ver). Mais il y a un hic. Regardons l'intervalle sur une ligne d'univers de u, theta et phi constant :



Si alpha est négligeable devant u² (donc u très grand en valeur absolue, donc R très grand), et on a simplement , la coordonnée t est donc concordante avec la mesure du temps propre si on est très loin. Plus u est petit en valeur absolue, plus la durée propre écoulée pour un même écart de coordonnée t est petite, c'est l'effet Einstein. Le problème se pose quand u=0 : l'intervalle est nul. Resterait à déterminer si c'est parce que la ligne u=0 ne représente qu'un unique évènement où si c'est parce que la ligne u=0 est de genre nul (la réponse étant connue cependant).
Néanmoins, dans les deux cas, rien ne va d'un côté à l'autre du diabolo (si ce n'est des géodésiques de genre espace qu'aucune particule ne peut suivre, avec ou sans masse), et des lignes d'univers vont d'une valeur finie de u à u=0, ou inversement, en une durée propre finie (elles vont vers t infini ou arrivent de t -infini), mais elles ne se poursuivent pas dans les u négatifs si elles viennent des u positifs et vice-versa.

m@ch3

[Amanuensis]

La singularité de coordonnée disparait (vu de Kruskal-Szekeres, on couvre les régions I et III

On notera donc que l'espace-temps défini par cette métrique, avec t et u parcourant tous deux R ne présente pas de singularité de coordonnées, mais n'est pas complet.

Comme déjà mentionné, ce n'est pas r=r_s et t fini qui exige physiquement une extension (1). Faut pas confondre la singularité de coordonnée et le besoin d'extension.

Et ce n'est pas parce que le domaine de définition de (t, u) est R² que la solution n'est pas extensible. Certes on ne peut pas garder la coordonnée t et étendre l'espace. Mais rien n'oblige à garder la coordonnée t...

(1) Point intéressant: il est physiquement difficilement acceptable d'avoir des lignes causales extensibles. Mais pourrait-on accepter, du point de vue physique, des lignes non causales extensibles? Je pense que oui. Autrement dit, en résolvant r_s=0 t fini, on n'a pas vraiment progresser du point de vue physique...