Bonjour,
J'ai vu plusieurs discussions sur le sujet. Mais il n'y avait pas de calcul explicatif.
J'ai essayé de faire des hypothèses et quelques calculs qui me semblent intéressants.
En résumé :
* une ampoule à LED de 10 W a une résistance équivalente de 6KOhm environ.
* la capacité parasite entre phase et neutre est de l'ordre de 0,5 µF / k avec k le facteur de réduction de la tension u=240 V (cela veut dire que si on trouve une tension aux bornes de la lampe de 60 volts, ce facteur k est de 240V / 60V = 4)
* pour réduire la tension parasite aux bornes de la lampe d'un facteur k*, il faut mettre en parallèle de la lampe un condensateur de valeur C* = k* . 0,5 µF (formule approximative, si k* >=3, et pour une puissance de 10 W). Cela veut dire que si on veut faire baisser cette tension de 60V d'un facteur 3, il faudrait mettre un condensateur de 3 * 0,5 = 1,5 µF (pour une lampe de puissance 10 W).
J'ai fait cela car j'avais besoin de mieux comprendre. J'espère que mes calculs ne sont pas faux et que les conclusions sont justes. Je pense retrouver des valeurs de capacités qui sont suggérées pour réduire le phénomène.
Détails :
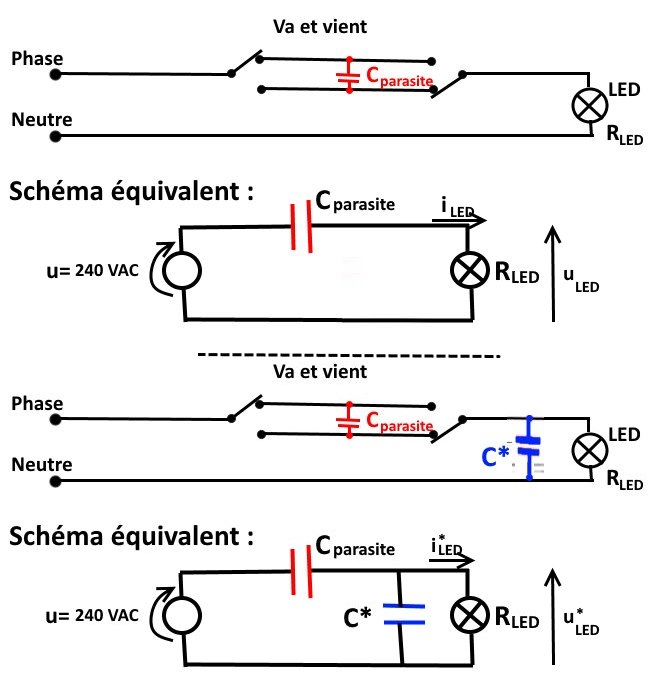
voici un schéma électrique équivalent :
Et voici mes calculs :
(j'espère qu'ils ne sont pas trop faux...)
Si on fait l’hypothèse que le courant résiduel est dû à une capacité parasite entre les 2 fils du va-et-vient ( Cparasite en rouge sur le schéma), on voit alors qu’il peut passer un courant dans l’ampoule à LED.
On voit aussi que si on intervertit la phase et le neutre, cela ne devrait pas faire grand-chose (le schéma équivalent ne change pas vraiment car les 2 fils du va et vient n’ont pas bougé physiquement). Donc, cela ne devrait pas supprimer le phénomène de lampe qui reste allumée.
Rem : J’ai encore un doute sur la bonne compréhension du phénomène. Je me demande si il n’y a pas également un phénomène inductif (une boucle qui, par induction à cause des champs magnétiques créés par les fils, crée une force électromotrice aux bornes de la lampe). Car le fil de neutre qui va directement à la lampe ne longe pas obligatoirement le fil de phase, ce qui peut créer une grande boucle. Les calculs suivants ne prennent pas cela en compte.
1/ Calcul de la résistance équivalente de la lampe LED :
La puissance d’une lampe led est : P_LED = U² / R_LED
D’où : R_LED = U² / P_LED = 6 Kohm environ
(en prenant P_LED de l’ordre de 10 W, et U = 240 V)
2/ Cherchons une évaluation de ce condensateur parasite :
On ne met pas encore de condensateur C*.
L’ampoule claire faiblement. Soit k le paramètre tel que la tension parasite soit k fois moins grand que la tension u de 240 VAC en mode éclairage normal. On a :
u_LED_parasite = u / k
Appliquons la formule du pont diviseur à u_LED_parasite :
R_LED / (z_parasite + Rled ) . u = u / k
D’où : z_parasite + Rled = Rled * k
En prenant la norme de ces impédances complexes, on a :
z_parasite² + R_LED ² = R_LED² . k²
z_parasite² = R_LED² . ( k² - 1)
!!z_parasite !! = R_LED . racine( k² - 1)
Or, Z_parasite = 1/jwC_parasite
D’où : C_parasite = (1/racine(k²-1) ) * ( 1/ (w * R_LED) )
On peut simplifier racine(k2-1) : si k>=3 (courant 3 fois plus faible) on a : racine(k²-1) = k à 20% près
D’où : C_parasite = ( 1/ (k *w * R_LED)
en remplaçant la pulsation w et R_LED, on obtient :
C_parasite = 0,5 µF / k (approximation pour k >=3)
(si le courant parasite dans la LED est 5 fois plus faible que le courant en mode allumé, cela veut dire que le condensateur parasite est de 0,5 / 5 = 0,1 µF
3/ Ajoutons un condensateur C* pour limiter le phénomène :
Sans ajouter de capacité, on a : u_LED = R_LED . i_LED
Avec la capacité C*, on a : u*_LED = R_LED . i*_LED
Appelons k* le coefficient tel que u*_LED = u_LED / k*
Cherchons la valeur du condensateur C* permettant de réduire la tension aux bornes de la lampe d’un facteur k* :
u*_LED = u_LED / k*
appliquons la formule du pont diviseur et remplaçons u*_LED, et aussi utilisons u_LED = u / k :
u . ( z*//R _LED ) / ( z*//R_LED + z_parasite) = ( u / k ) / k*
( z*//R _LED ) / ( z*//R_LED + z_parasite) = 1 / (k . k*)
k . k* ( z*//R _LED ) = ( z*//R_LED + z_parasite)
Je fini par une formule du style :
1/z* = (k . k* - 1) / z_parasite - 1 / R_LED
En remplacant 1/z* par j w C* et 1 / z_parasite par j w Cparasite
C* = (k . k* -1) . Cparasite + j / (w .R_LED)
Soit : C* = racine[ (k.k* - 1)² C parasite² + 1 /(w. R_LED)² ]
C* = racine[ (k.k*)² Cparasite² + 1 / (w . R_LED)² ] (si on fait l’hypothèse que k.k* > 3)
En effectuant les calculs :
C* = racine[ (k*² (0,5 µF)² + (0,5 µF)² ]
Je fini par trouver qu’il faut prendre un condensateur de (surtout si on dit : k* >3) :
C* = k* . 0,5µF environ
Donc, si on veut réduire le courant passant dans la led d’un facteur 3, il faut prendre C* = 3 x 0,5 µF
-----