vibration des trous noirs

[Zefram Cochrane]

Bonjour,
dans le cadre de la métrique de Schwarschild et d'une chute libre depuis la coordonnée de départ Ro, je peux calculer
d'où la vitesse instantanée du chuteur
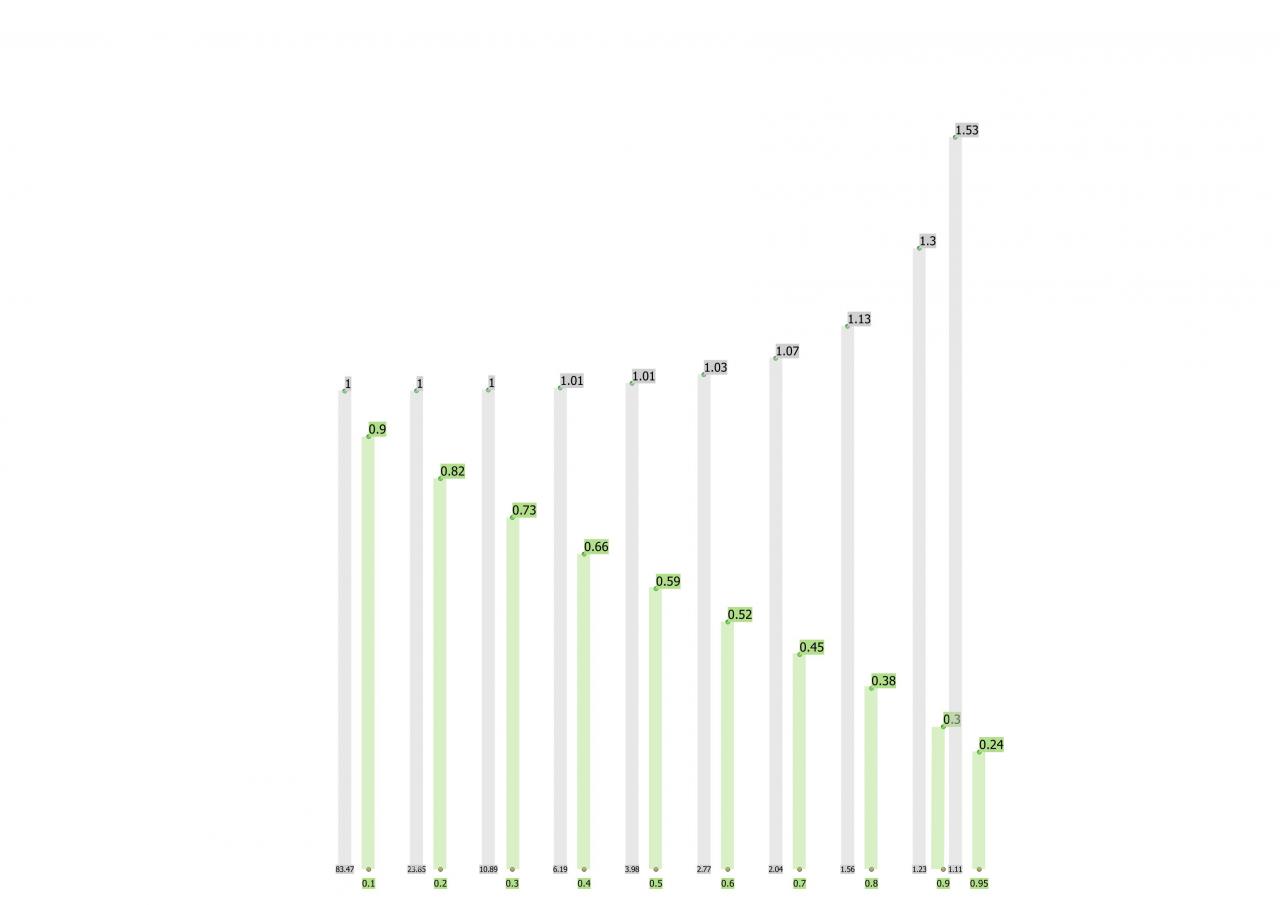
et d'où la relation entre la coordonnée R et la vitesse instantanée :

pour on a R = Rs et ce indendamment de la coordonnée de départ Ro.

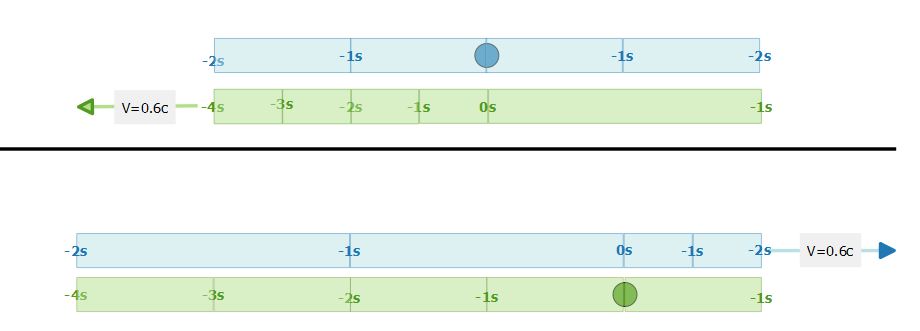
Autrement dit si on imagine un astre dense avec un rayon proche de Rs et à la surface duquel sont empilés verticalement des sections cylindriques la vitesse du chuteur lorsqu'il arrivera un niveau du sol tendra vers la vitesse de la lumière.
ce qui pose le problème d'un astre gelé puisque si le temps semble gelé à la surface d'un TN, si on augmente encore la densité de l'astre dense tel que son rayon devienne égal à Rs. un observateur situé au niveau d'un cylindre ne verra jamais celui situé à la base de la pile chuter dans l'astre dense devenu TN.
mais, la contradition se lève de plusieurs manière je pense parce que si le temps se gèle à la base de la pile, cela veut dire que le cylindre à la base est infiniment redschifté donc disparaît et comme le temps n'est pas gelé pour celui du dessus, il peut entamer une chute libre dans le vide du premier cylindre entraînant le reste de la piledans sa chute.
Un observateur siuté dans le cylindre de base lorsqu'il entamera sa chute aura une vitesse relative par rapport au cylindre situé juste au dessus égal à la vitesse de la lumière, donc, en partant de l'hypothèse qu'il chute à c depuis l'horizon du TN jusqu'à la singularité centrale, il ne verra jamais le second cylindre de la pile commencer à chuter. ( à confirmer SVP)
l'autre point concerne le rayonnement de hawking : est-il possible? qu'un TN pulse du fait qu'il aie un température de surface non nulle et qu'il y ai finalement un écoulement de temps propre même très faible?
-----

[Mailou75]

Salut Zef,

Je n’ai pas la réponse à ta question mais je vois au moins deux incohérences dans l’énoncé du problème :

- Tu ajoutes de la masse (energie ) au système en cours d’expérience. C’est interdit et c’est la cause de ton problème, mais j’imagine que tu le savais...

- Tu parles d’une vitesse de chute vallant c au passage en Rs. Attention cette vitesse vaut c (45°) dans un repère de Painlevé (~ Newton avec lumière courbe), c’est donc dr/dTau. Si tu regardes ici https://forums.futura-sciences.com/a...ml#post5882616 graph de gauche, tu vois que la lumière entrante (rayon bleu) a un angle superieur à 45°, c’est Vert qui est à 45°. Il ne va donc pas aussi vite que la lumière.

[Zefram Cochrane]

Bonsoir,
on avait calculé que la vitesse coordonnée pour un observateur à l’oo( vitesse apparente du chuteur pour l’observateur à l’oo) est:

et nous avions calculé que

J’ai du mal à interpréter le sens physique de cette formule parce que pour moi elle ne correspond à rien de mesurable.
Nous avions également calculé la longueur propre d’une corde tendue depuis une station spatiale sationnaire à la coordonnée Ro jusqu’à l’horizon du TN en faisant l’intégration suivante:

Donc en imaginant que chaque cylindre à une longueur propre
on a la relation:

Ce qui correspond à la vitesse à laquelle le chuteur voit défiler une longueur de cylindre en une durée ; cela correspond donc à la célérité, c’est-à-dire:

d’où
quand , R → Rs.

La vitesse que je mentionne n'est pas mais c'est la vitesse de passage du chuteur à l'horizon du TN. On a la même chose avec Rindler :
tu as un train de wagons automoteurs stationnaire initialement le long d'un quai inertiel de grande longueur.
à T=0s, les wagons accélèrent et l'observateur du quai situé à T=0s en tête de train calcule la vitesse de défilement des wagons à partir de sa montre. Si le dernier wagon était proche de l'horizon de Rindler, l'observateur le verra défiler avec une célérité presque infinie, soit une vitesse instantanée proche de la vitesse de la lumière.

Pour le premier point que tu mentionnais on imagine qu'un petit lutin s'amuse depuis une position éloignée de l'autre coté de l'astre dense à envoyer de l'énergie pour en augmenter la densité jusqu'à atteindre un poids critique.
@+
Zef

[Pio2001]

ce qui pose le problème d'un astre gelé puisque si le temps semble gelé à la surface d'un TN, si on augmente encore la densité de l'astre dense tel que son rayon devienne égal à Rs. un observateur situé au niveau d'un cylindre ne verra jamais celui situé à la base de la pile chuter dans l'astre dense devenu TN.

Bonjour Zefram,
Dans une vieille discussion à présent verrouillée, Mach3 laissait entendre que dans le cas particulier d'un trou noir "en croissance", on pourrait voir l'horizon, qui grossit, avaler des objets :

si on regarde un objet chuter vers un trou noir en croissance, on le verra disparaitre une fois que le trou noir aura grossi.

[A voir en vidéo sur Futura]

[Mailou75]

Salut,

Je ne suis pas trop d’accord avec ton histoire de corde tendue. Si tu peux tendre une corde entre les obervateurs a r constant se sera ton espace «rigide» (au sens corde de Bell). La longueur de cette corde c’est la parabole de Flamm. C’est une somme de petites longueurs locales, mais ce sont les longueurs percues par les r constants.

L’observateur eloigné voit ces longueurs contractées de z+1 (beaucoup proche de l’horizon et peu juste devant lui). Comme tu le sais le Y (gamma) de la chute libre depuis l’infini vaut en tout point de la chute... z+1! Celui qui chute voit* les longueurs locales compressées de Y, il voit donc les mêmes r que l’observateur éloigné. Enfin je crois...

* voit juste sous ses pieds, ce qu’il voit au loin est un autre sujet

A plus

Mailou

[Zefram Cochrane]

Bonjour,

Je ne suis pas trop d’accord avec ton histoire de corde tendue. Si tu peux tendre une corde entre les obervateurs a r constant se sera ton espace «rigide» (au sens corde de Bell). La longueur de cette corde c’est la parabole de Flamm. C’est une somme de petites longueurs locales, mais ce sont les longueurs percues par les r constants.

Cela veut dire dans le cadre de mon exemple que si l'observateur situé dans le cylindre de longueur dr situé au sommet de la pile demande à un peintre de prendre des bandes de couleur tous les dr et commençant par le haut, le peintre peindra la section situé à l'intersection des deux cylindres situés en hauteur et au fur et à mesure qu'il descendra peindre une bande tous les (z+1) longueur propre de cylindre.
D'où :

L’observateur eloigné voit ces longueurs contractées de z+1 (beaucoup proche de l’horizon et peu juste devant lui).

Donc c'est comme en RR, si un cylindre fait 4s de longueur propre, Bleu qui chute vers la droite se trouve au milieu de son cylindre et lorsqu'il croise Vert (qui se trouve à la base du sien mais il y a un quart de longueur d'un autre cylindre peinte en dessous), il voit sont cylindre occuper 5/4 fois la longueur d'un cylindre stationnaire.

Comme tu le sais le Y (gamma) de la chute libre depuis l’infini vaut en tout point de la chute... z+1! Celui qui chute voit* les longueurs locales compressées de Y, il voit donc les mêmes r que l’observateur éloigné. Enfin je crois...
* voit juste sous ses pieds, ce qu’il voit au loin est un autre sujet

Comme en RR, à tout instant propre tau, il voit défiler la pile de cylindre avec une certaine célérité, d'où la vitesse instantanée qui en découle.

Bonjour Zefram,
Dans une vieille discussion à présent verrouillée, Mach3 laissait entendre que dans le cas particulier d'un trou noir "en croissance", on pourrait voir l'horizon, qui grossit, avaler des objets :

Oui parce que la masse du TN est proportionnel au rayon dans le cadre de la métrique de Schwarzchild ( le mécanisme de grossissement du TN n'est pas connu me semble t'il).
Par contre je ne crois pas que cela explique pourquoi le second cylindre va démarrer sa chute.
Quand je parle de "disparition", j'entends "cesse d'être causalement influencé par".

Le cylindre à la base de la pile qui se trouve à la surface de l'astre dense verra cette surface disparaître lorsque la densité sera suffisante pour transformer l'astre dense en TN.
Et, comme il est proche de la surface du TN, il atteint rapidement la vitesse de la lumière par rapport au second cylindre. L'obsrvateur du premier cylindre voit donc le second cylindre disparaître.
Le second cylindre voit le premier cylindre chuter, donc il chute également. En atteignant l'horizon d'un TN sa vitesse instantanée est c par rapport à un observateur qui serait stationnaire juste au dessus de l'horizon du TN. Cet observateur voyant le troisième cylindre arriver vers lui à une vitesse <c, je ne vois pas pour quelle raison, à l'instant où le second cylindre passe l'horizon du TN, sa vitesse realtive par rapport au troisième cylindre serait différente de c.
Et ainsi de suite...

[Mailou75]

Salut,

Désolé mais ce n’est pas limpide... tu parles de haut/bas puis droite/gauche, tout à coup on a un 5/4 parachuté sans aucune application numérique, je ne comprend rien à tes schémas etc...

Si tu le veux bien démarre avec un trou noir déjà formé et donne des valeurs à tes dr. Je ne saurais participer à une discussion sur un «modèle*d’effondrement» car ce modèle n’existe pas (ou présente toi au Nobel) donc pas d’ajout de masse en cours d’experience stp.

[yves95210]

Je ne saurais participer à une discussion sur un «modèle*d’effondrement» car ce modèle n’existe pas (ou présente toi au Nobel) donc pas d’ajout de masse en cours d’experience stp.

Enfin si, le modèle d'effondrement existe, et correspond certainement à une réalité physique.
Mais effectivement il ne nécessite pas d'"ajout de masse" (sauf si on parle de la partie de la masse initiale de l'étoile qui se retrouve progressivement sous l'horizon des évènements).

[Mailou75]

Ajouter de la masse a volume égal ou reduire le volume a masse égale pour moi c’est kif kif, c’est un effondrement. Non je ne crois pas que le modèle existe, on fait s’effondrer des «coques de photons» ou de particules mais a aucun moment une boule pleine. Pour ça il faudrait que le diagramme affiche une phase de supernova, je n’en ai jamais vu de tels. M’est d’avis que quand on aura un modèle pour ça on aura peut être un modèle pour autre chose...

Mais l’idée n’est pas de s’éloigner du sujet. Je cherche au contraire a simplifier l’ennoncé pour que le problème posé soit «traitable» avec les formules dont on dispose aujourd’hui.

[yves95210]

Non je ne crois pas que le modèle existe, on fait s’effondrer des «coques de photons» ou de particules mais a aucun moment une boule pleine.

L'idée que tu te fais d'une étoile m'a l'air un peu bizarre. Faudrait que tu consultes un astrophysicien (ça serait bien s'il y en avait un qui passait par là de temps en temps).

Mais l’idée n’est pas de s’éloigner du sujet. Je cherche au contraire a simplifier l’ennoncé pour que le problème posé soit «traitable» avec les formules dont on dispose aujourd’hui.

Hors-sujet par rapport à votre discussion, peut-être, mais pas par rapport à la vocation du forum "Astronomie et Astrophysique" (et non "modèles basés sur la RG sans rapport avec la réalité physique")...

Mais bon, je ne voudrais pas déranger.

[Mailou75]

Tu déranges pas. Je voulais juste dire que les coques qu’on fait s’effondrer sont vides. Aucune ne décrit d’épisode nova, si tu trouves que ça colle à la réalité...

[JPL]

Faudrait que tu consultes un astrophysicien (ça serait bien s'il y en avait un qui passait par là de temps en temps).

Ceux qui ont essayé sont repartis dégoûtés.

[Zefram Cochrane]

Bonsoir,
Amanuensis m'a fait remarquer un jour que la métrique de Schwarzschild décrivait un TN éternel dans un espace infini.
Cela ne me paraît non plus un cas de figure très réaliste. Pourtant le modèle qui sert de base à la métrique de Kerr donne plutôt de bons résultats.
En attendant, j'ai fais un schéma.
J'ai pris Rs = 1s.l et comme altitude de départ Rmax = 500s.l
ensuite grâce à ma formule, j'ai calculé Ro pour des vitesses V allant de 0.1c à 0.95c.
Grâce à cette formule :
https://forums.futura-sciences.com/a...ml#post4613724
j'ai calculé la longueur propre séparant le Stationnaire de l'horizon du TN.
Après, j'ai considéré que le Stationnaire était à la base d'un tube de 1s.l de longueur propre de hauteur et j'ai du rechercher manuellement qu'elle était la coordonnée Ri correspondante au sommet du tube.
Après grâce à dr'=1/RACINE(1-Rs/Ro) , j'ai calculé la distance apparente séparant le Stationnaire du sommet du tube.
Enfin, j'ai calculé grâce au TLs (EDR) , à quelle distance apparente le chuteur (qui chute depuis Rmax) voit le sommet du tube lorsqu'il passe le travers du Stationnaire à V.

en bas du tube gris se trouve la coordonnée Ro du Stationnaire, en haut la hauteur apparente du tube de son point de vue; en bas du tube vert se trouve la vitesse atteinte par le chuteur et au sommet, la hauteur apparente du tube de son point de vue.

[Mailou75]

Salut,

Faut se creuser la tête pour te suivre... je vais essayer de résumer ce que je comprends :

- Le trou noir a un rayon Rs=1sl
- On fait partir des voyageurs en chute libre depuis une coordonnée r=500Rs (on cherche une approximation d'un observateur à l'infini ?)
- On cherche à quelle altitude r=Ro ils auront atteint une vitesse donnée (V est la donnée d'entrée)
- On place pour chaque Ro (de chaque V) un tube longueur propre locale L'=1sl (Un peu grand pour parler d'infinitésimal avec un Rs de la même taille...)
- On calcule la coordonnée r=Ri du sommet du tube (soit la longueur apparente du tube pour l'observateur éloigné L=Ri-Ro < L')
- On calcule la distance apparente entre Ro et Ri (longueur du tube) pour le stationnaire en Ro (on vient de faire deux opérations inverse étrange qu'on ne retombe pas sur L')
- On calcule la distance propre qu'occupera le tube dans l'espace du voyageur en chute libre (compression de la longueur propre du tube, on doit retomber sur L)

J'ai du mal à comprendre l'expérience et sa complexité m'interroge sur ce qu'elle cherche à prouver... mais j'ai regardé tes chiffres et ce qu'il disent c'est (je prends 0,8c en application numérique) :

- Ro=1,56 est bien l'altitude à laquelle un objet lâché de l'infini atteint B=0,8 car z+1=rac(1-1/1,56)=0,6=1/Y
- Ensuite je ne sais pas trop ce que tu fais mais on dirait que tu appliques une aberration redshift (z+1=3) sur une longueur impropre soit 1,13/3=0,38. Je ne pense pas que ceci soit autorisé...

C'est plus simple que tu ne l'imagines en fait :

- D'après ce que j'en ai compris, chez Schw, r est la longueur vue par l'observateur éloigné disons un intervalle de dr=1sl (même je préfèrerait diminuer cette longueur car l'expérience ne montrerait rien)
- Localement cet intervalle vaut dr'=dr/(z+1) il est plus long, à Ro=1,56 il vaut dr'=1,66sl avec des règles locales
- Quand le voyageur traverse cette longueur propre elle sera compressée de 1/Y soit... dr=1sl (et c'est pour ça que le trajectoires de chute sont newtoniennes, sinon ça n'aurait aucun sens)
- En espérant ne pas me tromper je dirais que c'est à chaque fois des distances qui sont vues ET qui pourraient être mesurées avec des mètres locaux (mais ton expérience ne l'est pas) ou en mouvements

Je ne crois pas être le mieux placé pour te répondre, je patauge encore, mais déjà si tu fais un énoncé compréhensible et une petite application numérique (qui évite les Ro, Ri etc) tu as plus de chance de recevoir de l'aide

Bon courage