L'argument de Schild pour la nonexistence des referentiels de Lorentz sur terre

[mahoumaru]

Salut,

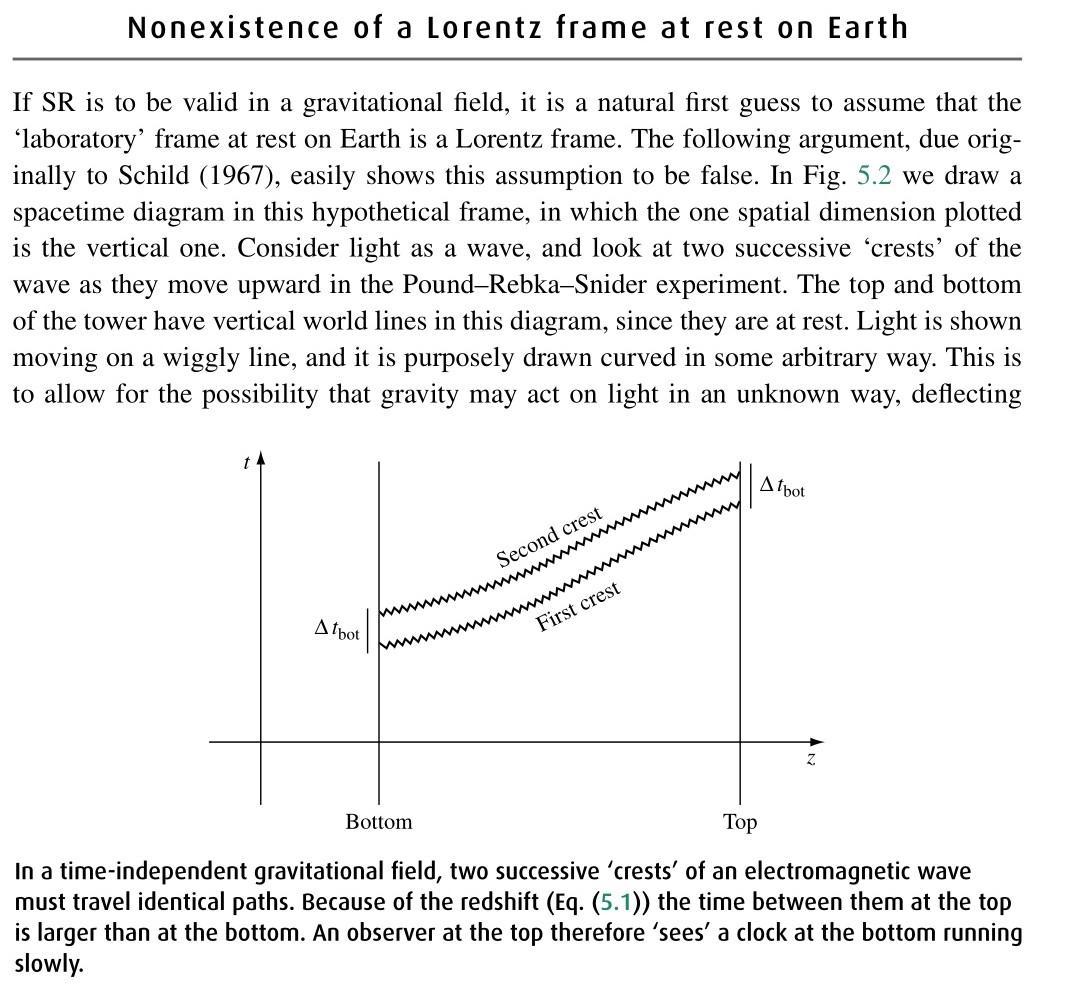
Comment cela se fait-il que dans son livre "A first course in general relativity", au chapitre 5 (preface to Curvature), pour illustrer l'argument de Schild, Schutz ait pu dessiner des world line (désolé, je me souviens plus de l’appellation en français) courbés pour les photons? Un extrait du livre sur Google books

Cela ne viole-t-il pas le postulat qui veut que la vitesse de la lumière soit la même dans tous les référentiels (ce qui veut dire, d'après ce que j'ai compris, que v = c = 1 et donc que les world line d'un photon devrait toujours avoir une pente 1 dans le diagramme d'espace temps, ce qui n'est plus le cas, ou du moins, me semble ne plus être le cas si on trace des lignes courbées comme il l'a fait dans son illustration)?

Intrigué par ça, j'ai essayé de trouver une autre description de l'argument et j'ai trouvé ça sur einstein.stanford.edu:

To see why this is such a pivotal experiment for general relativity, consider the following simplified experiment. Imagine two experimenters, Thelma and Louise, where Thelma is standing on the ground and Louise is on top of a tall step ladder. Thelma sends exactly 10 cycles of yellow light to Louise, who then waits until her equipment has registered all 10 beats of the light. Because the light signal Louise received has lost some energy climbing up the earth's gravity well to the top of the ladder, it has been red shifted to a lower frequency. Louise has to wait longer than it took Thelma to send all ten beats of the light signal in the first place. The reason that this experiment contradicts special relativity is because, first of all, both Thelma and Louise are at rest relative to each other. They are moving with exactly zero velocity with respect to each other. This means that they share exactly the same reference frame in special relativity. But, this necessarily means that a single, flat space-time patch should be exactly sufficient upon which to describe both their world lines, and those of the wavelets in the light ray they exchanged. Their world lines should form the opposite sides of a rectangle in which the light ray forms the diagonal. By a simple geometric construction, however, we see that this cannot occur because the light wavelets take longer to receive than to send. This can only be accommodated if the space-time patch is not flat, thereby showing that the gravitational redshift demands space-time curvature. This is a direct deduction from observation, and is the essential underpinning of the entire rubric of curved space-time.

Ici, ils parlent de diagonal (donc, je suppose, de lignes droites), ce qui correspond à ce que j'ai compris des explications de Schutz, indépendamment de l'illustration qu'il a utilisé.

Mais j'aimerais comprendre comment c'est possible de dessiner une world line courbée pour un photon comme il l'a fait dans son livre et donc, ce que je n'ai pas bien saisi.
Merci d'avance.
-----

[yves95210]

Salut,

Cela ne viole-t-il pas le postulat qui veut que la vitesse de la lumière soit la même dans tous les référentiels (ce qui veut dire, d'après ce que j'ai compris, que v = c = 1 et donc que les world line d'un photon devrait toujours avoir une pente 1 dans le diagramme d'espace temps, ce qui n'est plus le cas, ou du moins, me semble ne plus être le cas si on trace des lignes courbées comme il l'a fait dans son illustration)?

Ce n'est qu'en espace-temps "plat" (celui de la relativité restreinte) que les lignes d'univers des photons (géodésiques de genre lumière) sont des droites dans le diagramme d'espace-temps.

Et le paragraphe que tu cites explique justement que, dans l'expérience proposée, le fait de représenter ces lignes d'univers par des droites conduit à une contradiction, d'où la conclusion que localement (à l'échelle de l'expérience) l'espace-temps n'est pas plat.

[mahoumaru]

Salut, merci pour ta réponse rapide.
Je tiens à préciser que ce n'est pas l'expérience en soit ou l'argument qui me pose des problèmes, mais le diagramme utilisé par Schutz !

L'argument de Schild consiste, si j'ai bien compris, à partir de l'hypothèse qu'on est dans un univers "plat" et de montrer que cela conduit à une contradiction avec les résultats de l'expérience menée. Selon ta réponse (et ce que je pensais déjà avoir compris), les lignes d'univers devraient être droites et non courbes. Ce serait donc une erreur de la part de l'auteur du livre ?

[yves95210]

Selon ta réponse (et ce que je pensais déjà avoir compris), les lignes d'univers devraient être droites et non courbes. Ce serait donc une erreur de la part de l'auteur du livre ?

Celles du diagramme dans le livre de Schulz ?
Je ne vois pas de quelle figure tu parles, mais seules certaines pages du livre sont accessibles sur google books. Mais si le diagramme est censé illustrer l'argument de Schild aboutissant à une contradiction (et non donner la solution correcte), effectivement les lignes d'univers devraient être droites.

[A voir en vidéo sur Futura]

[Nicophil]

Bonjour,

ce qui n'est plus le cas, ou du moins, me semble ne plus être le cas si on trace des lignes courbées comme il l'a fait dans son illustration)?

Si si, sa ligne est courbée mais la particule n'accélère pas.

[Matmat]

ça signifie juste que l'argument "il n'y a pas d'accélération cinématique de thelma par rapport à louise" n'est pas suffisant pour considérer que les diagrammes de minkowski représentent exactement la situation

(...They are moving with exactly zero velocity with respect to each other. This means that they share exactly the same reference frame in special relativity )

[mahoumaru]

Bonjour,

Si si, sa ligne est courbée mais la particule n'accélère pas.

ça signifie juste que l'argument "il n'y a pas d'accélération cinématique de thelma par rapport à louise" n'est pas suffisant pour considérer que les diagrammes de minkowski représentent exactement la situation

(...They are moving with exactly zero velocity with respect to each other. This means that they share exactly the same reference frame in special relativity )

Hum, je suis désolé, mais je ne suis plus sûr de comprendre.
Comment la ligne peut elle être courbée (donc avec changement de pente), si la particule n'accelere pas ?

@Matmat, je crois comprendre un peu ce que tu veux dire (il s'agit de la raison de la raison de l'échec de la RR, non ?), mais cela ne me dit pas vraiment comment les lignes d'univers des photons peuvent être courbées, sans que cela implique un changement de vitesse ?

@yves, merci pour ta réponse. Désolé que la partie concernée n'apparaisse pas. Voici une image de ce dont je parle :

[mach3]

Dans le MTW, pages 187 à 189, l'argument de Schild est présenté en deux temps. D'abord on considère que les rayons lumineux sont des droites. On obtient un parallélogramme, dont les côté opposés de genre temps devrait faire la même durée, sauf qu'on sait que ce n'est pas le cas (mesure expérimentale du redshift), donc on peut en déduire que l'espace-temps n'est pas plat.

Cependant, on pourrait rétorquer que c'est parce la gravité modifie le comportement de la lumière. Pour prendre en compte cela on admet que les rayons, au lieu d'être droits, pourrait avoir une forme différente, à cause de la gravité qui les modifierait (par exemple peut-être que la gravité change la valeur de c?), peu importe comment.

On peut alors reformuler l'argument, en accordant que les rayons sont peut-être courbes, mais dans ce cas, les deux rayons devraient être courbés de la même façon, ce qui fait que les deux côtés de genre temps de notre parallélogramme déformé devrait quand faire la même durée, contrairement à ce qu'on observe. Donc l'espace-temps ne peut pas être plat, même si on accorde que la lumière pourrait être influencée par gravité dans le cadre de la RR.

Au passage, un ancien fil à lire sur l'argument de Schild : https://forums.futura-sciences.com/p...sim-sabat.html

m@ch3

[mahoumaru]

@mach3,
Ah... d'accord ! Merci beaucoup pour la réponse et le lien (autant MWT, que l'ancien fil), là je crois avoir compris et je peux maintenant continuer ma lecture sereinement.

Merci à tous ceux qui ont répondu.