Bonjour à tous,
J'ai une question qui me trotte dans la tête que je n'arrive pas à éclaircir ^^
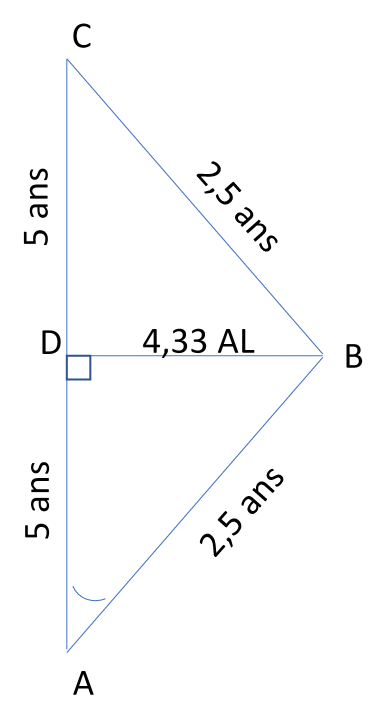
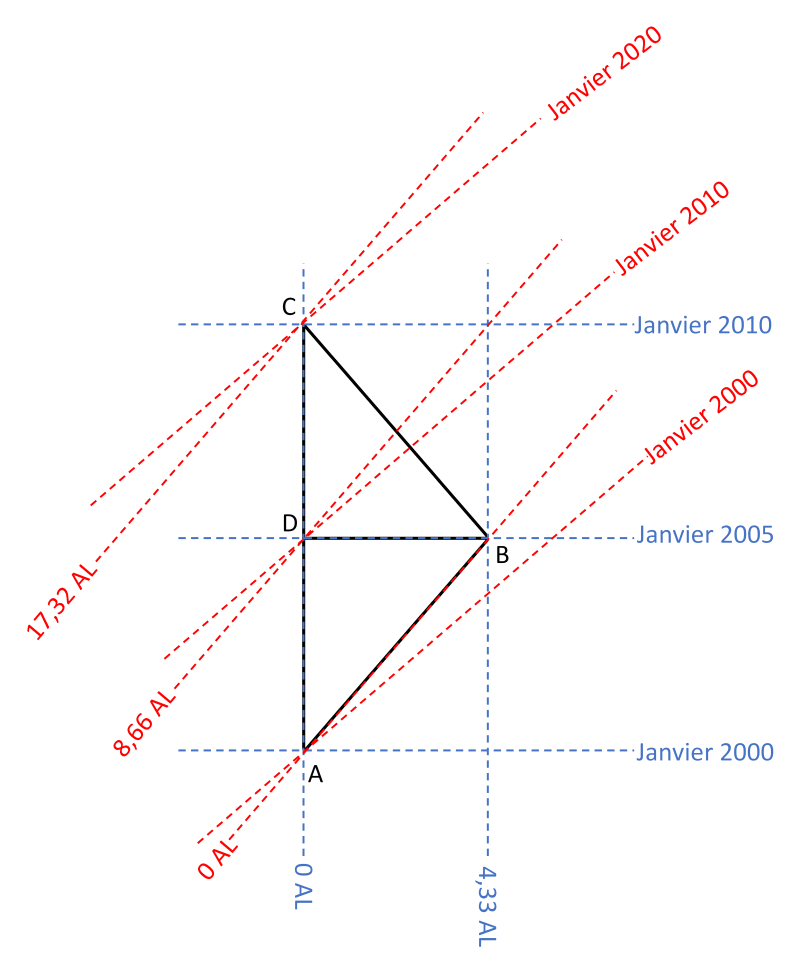
Si j'ai bien compris (dans les très grande lignes) la relativité restreinte, c'est que si on considère un point A avec une horloge et un point B avec une autre horloge qui sont synchronisées et que le point B fait un petit voyage dans l'espace avec une vitesse proche de C, alors lorsqu'il va revenir près de A leurs 2 horloges ne seront plus synchronisée, celle de B aura moins avancée que celle de A.
Mais ce que je ne comprends pas, c'est que si on se place du point de vue de B, c'est A qui se déplace à une vitesse proche de la lumière et qui revient.
Pourquoi ce serait l'horloge de B qui avancerait ? On m'a toujours dit que la vitesse était relative à un autre objet ^^. Du coup, pourquoi ce serait B qui se déplace ? quel moyen j'ai de savoir que c'est B qui va faire le voyage et non A ?
Merci d'avance de vos réponses
-----