Okay et merci. J'irai voir à l'occasion, mais pour les math en suivant l'histoire de la fourmi je me suis rendu compte que je comprenais pas la notion de différentielle donc c'est pas gagné
-----

Okay et merci. J'irai voir à l'occasion, mais pour les math en suivant l'histoire de la fourmi je me suis rendu compte que je comprenais pas la notion de différentielle donc c'est pas gagné

Bonjour, Pachacamac
Si j'en comprend un peu, avec une vitesse d'éloignement constante et égale à c sur le même axe, l'information est invariable et reste la même.

Pas tout à fait et ta formulation est trop flou.
Dans tous les cas même en dehors de ce problème lié à l’extension de l'univers l'information reste la même puisqu'il s’agit d'un photon ou d'un groupe de photons qui se propage dans le vide à la vitesse notée c de 300 000 km/s. On peut effectivement dire qu'ils se propagent selon un axe qui relie le lieu d’émission ( la galaxie qui a émis ces photons ) et le lieu de réception.( par exemple un télescope situé sur Terre ou sur un satellite). Au départ de ces photons la distance entre la galaxie et la Terre s’agrandit à une vitesse qui est plus grande que la leur c'est à dire c. ( à cause de l'expansion de l'univers )
mais la vitesse d’éloignement entre ces photons et la Terre n'est pas constante car elle dépend entre autre de la distance. Donc plus ces photons se rapprocherons de la Terre plus la vitesse d’éloignement entre eux et la Terre du à l'expansion va diminuer. Le "paradoxe" c'est que même si au départ ils avancent moins vite que le but ( la Terre ) s’éloigne, ils vont quand même arriver sur Terre.
C'est l'occasion ou jamais de dire c'est incroyable mais vrai !
Dernière modification par pachacamac ; 12/01/2023 à 20h04.

Un fil parmi d'autres, avec des liens vers d'autres fils, qui peut permettre d'y voir plus clair sur les différentielle : https://forums.futura-sciences.com/m...rentielle.html
m@ch3
Never feed the troll after midnight!

Bonjour Pachacamac
Et si tu reproduisais cette expérience en laboratoire en restant concentré seulement sur les deux éléments en éloignement, en oubliant l'Univers ?

@leopold11 : je n'ai pas de laboratoire, ni le matériel nécessaire (qui serait nécessairement sophistiqué), ni les comptétences pour réaliser cette expérience. Peut être que l'ESA ou la NASA qui ont pleins d'ingénieurs et de techniciens en mécanique et des spécialistes en caoutchouc pourrait la réaliser. (faudrait que tu demandes à Thomas Pesquet)
En plus simple il pourrait y avoir des simulations numériques ( il y en a une sur la page Wikipédia mais elle est pas très parlante).
@mach3 : merci pour le lien qui à l'air vraiment top pour aborder les différentielles.
Note que pour l'instant au niveau mathématique mon cerveau reste très occupé par le problème de la fourmi et de l’élastique. En plus, inconsciemment et à l'insu de mon plein gré, plutôt que d 'essayer de comprendre la démonstration il s'acharne à vouloir montrer que c'est impossible.
C'est dommage parce que je ne pourrais pas vous faire part de mes réflexions, qui s'appuient sur les première secondes de l’étirement et qui me semblent béton au niveau logique car elles vont vite être considérées hors charte par la modération.
Dernière modification par pachacamac ; 13/01/2023 à 11h50.

Bonjour,
je peux me tromper, mais le problème de la fourmi n'est pas l'analogue du problème de la propagation de la lumière dans un univers en expansion. En regardant vite fait la solution proposée sur wiki, on voit une résolution graphique du problème dans laquelle l'élastique s'allonge tout simplement de 2 cm chaque seconde (il passe de 4 à 6, 8 puis 10 cm....).
Ce n'est pas équivalent à l'élastique s'allonge avec un taux de 0,5 cm/s/cm. Au bout de la première seconde l'élastique mesure bien 6cm mais ça diverge après.
Yves avait proposé un problème plus "raccord" avec la cosmologie dans lequel une voiture roulant à vitesse constante v=100 km/h, part d'un point A pour aller à un point B séparés de 100 km à t=0, la route s'allongeant avec un taux de 0,1m/s/km.
On avait montré que dans ce cas c'était possible pour la voiture d'atteindre B, mais pour une séparation initiale entre A et B proche de 280 km ça ne l'était plus.
Discussion de 2022 à retrouver.

Salut Lansberg,
J'avais propose en #7 la même analogie que Yves mais avec A et B séparé de 1000km , la route s étend de 200 km/s et une voiture qui roule à 100 km/h j'y réfléchi encore.
Sinon pour l 'analogie élastique/expansion de l'univers, le problème est aussi abordé dans le forum "mathématiques-superieur"
Note pour la modération : merci de pas fermer un de ces forums pour cause de doublon, là bas on y discute de l'aspect mathématique du problème de la fourmi et ici de la récession des galaxies
Dans le dernier post de ce fil : quelqu'un pose aussi le problème de la validité de cette comparaison : je te recopie ce qu'il a écrit:
Re : le problème de la fourmi sur un élastique
Bonjour.
J'ai du mal aussi à voir le rapport entre l'histoire de la fourmi sur l'élastique et l'histoire de l'expansion de l'univers.
Sur wikipedia il est dit
Citation Envoyé par Wikipedia
Relation avec l'expansion de l'Univers
Compte tenu de l'expansion de l'Univers, on peut penser que la lumière de galaxies suffisamment lointaines pourrait ne jamais nous atteindre, particulièrement la lumière de celles qui s'éloignent de nous à une vitesse supérieure à celle de la lumière. Si l'expansion est uniforme, c'est-à-dire que chaque galaxie s'éloigne de nous à une vitesse proportionnelle à sa distance actuelle (et que cette vitesse ne change pas), on est dans la situation exacte du puzzle, ce qui montre que la lumière finira toujours par nous être visible. Cependant, dans l'état actuel de nos connaissances, l'expansion semble accélérer, et la logique du problème ne s'applique plus.
Or juste avant pour le problème de la fourmi sur l'élastique il est dit
Citation Envoyé par Wikipédia
Une fourmi (le point rouge) marchant sur l'élastique à la vitesse constante de 1 cm/s. L'élastique mesure initialement 4 cm et est étiré à vitesse constante de 2 cm/s.
Si je ne me trompe pas ces deux situations ne sont pas identiques.
1). Pour l'univers on a une expansion qui dépend de la distance et du temps : On ajoute une distance (qui n'est pas constante) qui dépend de la distance actuelle (multipliée par une constante) et ce par unité de temps.
Si on voit ça sous la forme d'une suite on a :
distance(t+1)=distance(t) + distance(t)*cst= distance(t)*(1+cst)
2). Pour l'élastique on a une expansion qui ne dépend pas de la distance mais juste du temps : On ajoute une distance (qui est constante) et ce par unité de temps.
distance(t+1)=distance(t) + cst
On a donc une suite géométrique pour 1). et une suite arithmétique pour 2).
L'analogie proposée par Wikipédia concernant la fourmi sur l'élastique et l'expansion de l'univers est-elle donc fausse ?

J'avais déjà failli la citer, mais Nicophil m'a grillé avec sa fourmi
Elle est là : https://forums.futura-sciences.com/d...e-lumiere.html, avec des contributions fort utiles de Archi3 et Lansberg
A lire en sautant une bonne partie des messages car la discussion avec Daniel1958 était partie un peu dans tous les sens, comme d'habitude (mais comme c'était un de ses premiers fils sur le forum on ne savait pas encore trop à qui on avait affaire, et que nos explications étaient peine perdue)...

Dans le cas de la fourmi, il faut comprendre que l'accroissement est constant (2 cm chaque seconde) mais le taux d'accroissement de l'allongement de l'élastique diminue (comme jusqu'à présent pour le taux d'expansion de l'univers ). À partir du moment ou la vitesse de déplacement de la fourmi reste constante, inexorablement elle se rapproche de l'extrémité de l'élastique.
C'est comme si on remboursait une dette qui s'accroit d'une somme constante au cours du temps avec un remboursement lui aussi constant. Avec le temps, on finit par honorer la dette car mécaniquement le taux d'intérêt tend vers 0.
Maintenant si le taux devient constant (comme dans le cas de l'expansion de l'univers dans un avenir lointain), il y a une limite au-delà de laquelle il devient impossible d'atteindre l'objectif.

Ce n'est pas la même situation. Dans le premier cas c'est le taux d'expansion qui est constant (ce qui correspond à une expansion accélérée), dans le second c'est la vitesse d'éloignement de l'extrémité de la route qui est constante, donc le taux d'expansion diminue constamment (et tend vers 0).Yves avait proposé un problème plus "raccord" avec la cosmologie dans lequel une voiture roulant à vitesse constante v=100 km/h, part d'un point A pour aller à un point B séparés de 100 km à t=0, la route s'allongeant avec un taux de 0,1m/s/km.
On avait montré que dans ce cas c'était possible pour la voiture d'atteindre B, mais pour une séparation initiale entre A et B proche de 280 km ça ne l'était plus.

Super ! On a ta résolution au message #51 pour un taux constant.J'avais déjà failli la citer, mais Nicophil m'a grillé avec sa fourmi
Elle est là : https://forums.futura-sciences.com/d...e-lumiere.html, avec des contributions fort utiles de Archi3 et Lansberg
A lire en sautant une bonne partie des messages car la discussion avec Daniel1958 était partie un peu dans tous les sens, comme d'habitude (mais comme c'était un de ses premiers fils sur le forum on ne savait pas encore trop à qui on avait affaire, et que nos explications étaient peine perdue)...
Je vois d'ailleurs une petite erreur dans l'intégrale de mon message #65. Il faut lire dx / (v - x/10000)


Recheche expérimentateur ou connaisseur des élastiques
J'ai trouvé une démonstration du problème de la fourmi que j'ai comprise entièrement sauf que j'ai un doute sur la validité de la première étape.
Si on prend un élastique mettons de 10 cm, qu'on fait une marque au dixième de sa longueur donc à 1 cm, puis qu'on étire l’élastique jusqu'à ce que sa longueur double et atteigne 20 cm.
Est ce que la marque faite à un cm va se trouver à deux centimètres de l'origine ?
Dernière modification par pachacamac ; 13/01/2023 à 14h43.

Bien sûr. Et une deuxième marque faite à 2 cm va se retrouver à 4 cm, etc.Recheche expérimentateur ou connaisseur des élastiques
J'ai trouvé une démonstration du problème de la fourmi que j'ai comprise entièrement sauf que j'ai un doute sur la validité de la première étape.
Si on prend un élastique mettons de 10 cm, qu'on fait une marque au dixième de sa longueur donc à 1 cm, puis qu'on étire l’élastique jusqu'à ce que sa longueur double et atteigne 20 cm.
Est ce que la marque faite à un cm va se trouver à deux centimètres de l'origine ?
C'est ce qu'on appelle coordonnées spatiales comobiles en cosmologie (sauf que l'élastique n'a qu'une dimension, et qu'on n'a donc besoin que d'une coordonnée spatiale).

Super le dernier fils conseillé ci-dessus ouvert par Daniel 1958. J'ai tout lu et les post recommandés # 51,58,60 et 65 ont répondu à tous mes questionnements sur cette question. J' en ai retenu aussi que si je veux entièrement les comprendre je n'ai d'autres choix que de faire de sérieuses révisons sur quelques bases élémentaires en math.
Sur le problème de la voiture qui roule à 100 km/h entre A et B séparé initialement de 1000km et qui s' étend de 200 km/s voici le résultat numérique :
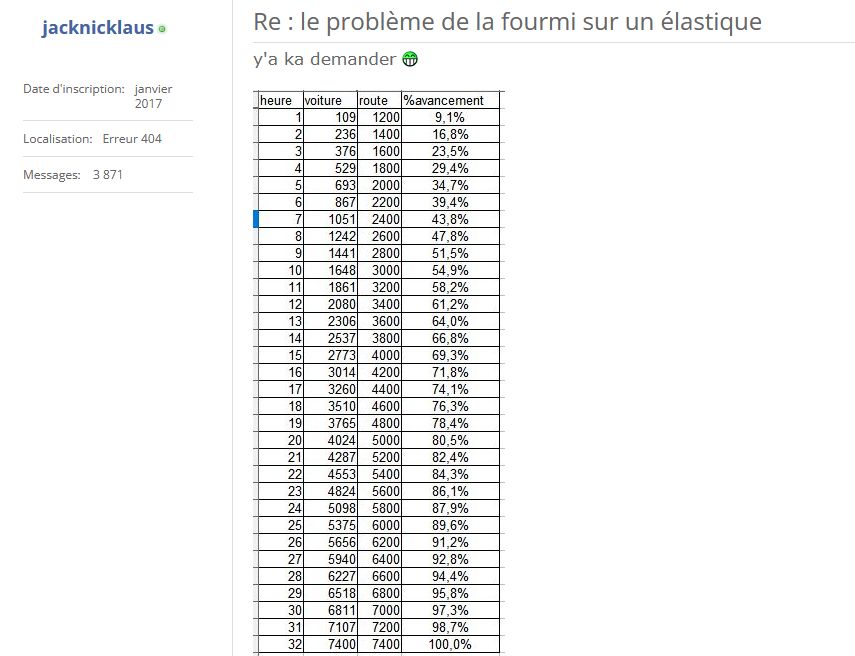

32 h de voyage seulement pour une route de 1000 km qui s'allonge de 200 km chaque seconde ??


Je confirme, la route s'allonge de 200 km par heure.
Aussi avec ce tableau si on soustrait la distance parcourue de la longueur de la route, on voit qu'au début la distance qui reste à parcourir augmente et c'est après 9 de route qu'elle commence à diminuer.

Je suis un peu perplexe.
Un expert pourrait-il valider ou infirmer les deux propositions suivantes ?
L'expansion de l'univers fonctionne comme ça :
1). On a une expansion qui vaut 1 par unité de temps.
Si entre deux points de l'espace on a une distance de 100 au temps 0 alors au temps 1 on a une distance de 101 et au temps 2 on a une distance de 102 et au temps 3 on a une distance de 103 etc.
2). On a une expansion qui vaut 1 par unité de temps pour 100 de distance (1 % par exemple).
Si entre deux points de l'espace on a une distance de 100 au temps 0 alors au temps 1 on a une distance de 101 et au temps 2 on a une distance de 101+ 101*1/100=102.1 et au temps 3 on a une distance de 102.1 + 102.1*1/100)= 103,121
Dans le cas 1). on a une progression arithmétique des distances et dans le cas 2). on a une progression géométrique des distances.
Quel est le bon modèle de l'expansion ?

@Pachacamac
Oui, ça colle cette fois !
t = d/v * (exp(v / v') -1)
d = 1000 km ; v = 200 km/h ; v' = 100 km/h
t = 1000/200 * ( exp(200/100) - 1 )= 31,94 h

Le paramètre qu'on utilise généralement est le taux d'expansion de l'univers (ou paramètre de Hubble), noté H.L'expansion de l'univers fonctionne comme ça :
1). On a une expansion qui vaut 1 par unité de temps.
Si entre deux points de l'espace on a une distance de 100 au temps 0 alors au temps 1 on a une distance de 101 et au temps 2 on a une distance de 102 et au temps 3 on a une distance de 103 etc.
2). On a une expansion qui vaut 1 par unité de temps pour 100 de distance (1 % par exemple).
Si entre deux points de l'espace on a une distance de 100 au temps 0 alors au temps 1 on a une distance de 101 et au temps 2 on a une distance de 101+ 101*1/100=102.1 et au temps 3 on a une distance de 102.1 + 102.1*1/100)= 103,121
Dans le cas 1). on a une progression arithmétique des distances et dans le cas 2). on a une progression géométrique des distances.
Quel est le bon modèle de l'expansion ?
Le cas 1) ci-dessus correspond à un taux d'expansion décroissant, puisque il vaut 1/100 par unité de temps à l'instant t=0, et par exemple il vaudra 1/200 par unité de temps à l'instant t=100.
Mais cet exemple n'obéit pas à l'équation de Friedmann (obtenue à partir de l'équation d'Einstein appliquée à un espace-temps spatialement homogène et isotrope), et ne peut donc pas être "le bon modèle".
En revanche si on applique la même règle à partir d'une distance nulle à l'instant t=0 (ce qui donne un taux d'expansion initial infini...), elle correspond à un des cas particuliers de l'équation de Friedmann, avec densité de matière nulle, courbure spatiale négative, et constante cosmologique nulle. Mais ce n'est toujours pas "le bon modèle" pour notre univers, puisque, selon les observations, sa courbure spatiale à grande échelle est nulle, ou en tout cas négligeable par rapport à sa densité de matière.
Le cas 2) correspond à un taux d'expansion constant 1/100, ce qu'on observerait (toujours selon l'équation de Friedmann) dans un univers vide de matière mais avec une constante cosmologique (ou densité d'"énergie noire") strictement positive. En fait notre univers finira par ressembler à ce modèle quand la matière se sera suffisamment diluée pour que sa densité d'énergie soit négligeable par rapport à celle de l'énergie noire.
De manière générale, l'équation de Friedmann dans un univers "de poussière", représentant notre univers observable (depuis l'époque du CMB), où la densité d'énergie du rayonnement est négligeable par rapport celle de la matière (ou "poussière"), s'écrit
oùest la densité d'énergie de la matière(*),
la constante cosmologique,
peut prendre les valeurs -1 (courbure spatiale négative), 0 (courbure nulle) ou 1 (courbure positive).
est le facteur d'échelle (croissant si l'univers est en expansion) et
, en notant
la dérivée de
par rapport au temps.
(*) autrement dit,est une masse volumique, et elle évolue comme
.

Je crois plus clair de répondre que c'est 2/ le bon raisonnement, mais avec un taux multiplicateur H qui décroit dans le temps (pour se stabiliser à une valeur constante dans le cas d'une cte cosmo positive).
Parcours Etranges

Merci pour cette confirmation.Envoyé par Gilgamesh
Je crois plus clair de répondre que c'est 2/ le bon raisonnement, mais avec un taux multiplicateur H qui décroit dans le temps (pour se stabiliser à une valeur constante dans le cas d'une cte cosmo positive).
J'étais en train de me faire des nœuds dans le cerveau ().
Même s'il est vrai que la réponse d'Yves95210 élargit les possibilité qu'on puisse obtenir une croissance qui ressemble à une suite arithmétique si le taux de croissance varie de manière adéquate dans le temps, je préfère quand même la version simple.
Est-ce qu'on peut résumer en posant que l'espace créé peut aussi être source de création d'espace ?
Pour le principe.
Comme lorsqu'on a de l'argent sur un compte bancaire, il y a également des intérêts à partir des intérêts.
Chaque euro compte dans l'accroissement et on ne se pose pas la question de son origine (est-ce que c'est un intérêt dont on ne doit pas tenir compte ou est-ce que c'est la somme qu'on avait initialement ?)
Ici l'accroissement des accroissements semble plus naturel.

pour faire simple : sans constante cosmologique, l'expansion ne serait ni linéaire, ni exponentielle (suivant la densité, R(t) finirait soit par croitre comme une puissance de t, soit s'arrêter et décroitre)
Avec constante cosmologique comme ça semble etre le cas, elle a aussi un comportement compliqué au début, elle commence par décélérer, puis réaccelérer , et finit par une croissance exponentielle quand la densité d'énergie est dominée par l'énergie du vide.
Donc aucun modèle simple de R(t) n'est applicable, et aucun ne correspond à un élastique qui croitrait en progression arithmétique ou géométrique (sauf l'état asymptotique avec la constante cosmologique mais on n'y est pas encore vraiment).
En revanche le résultat qualitatif qui est qu'un photon allant "localement à c" peut rejoindre un objet distant même si sa vitesse de récession a toujours été > c reste valable et est similaire au moins qualitativement au problème de la fourmi sur l'élastique.
Après pour aller plus loin il faut accepter de se plonger un peu dans les expressions mathématiques et connaitre un peu le comportement des intégrales ...

Les "un peu" sont bien évidemment des euphémismes, c'est de la plongée en eau très profonde.


C'est une interprétation possible de la constante cosmologique : un capacité de l'espace à créer de l'espace, qu'on peut interpréter comme une gravité répulsive. C'est sous cette forme que Einstein l'a introduite dans son équation.
Mais il y a en fait deux interprétations possibles :
* la première comme on vient de le voir est d'en faire une caractéristique sui generis de l'espace, c'est l'interprétation géométrique de Λ qui à la dimension L-2, l'inverse du carré d'une longueur. On la met à gauche de l'équation, côté tenseur d'Einstein (Rµν + 1/2 Rgµν), qui représente l'espace-temps, le contenant, donc la géométrie.
Rµν + 1/2 Rgµν + Λgµν = κTµν
* la seconde, qui a l'avantage de faire le lien avec la théorie quantique des champs (TQC), est d'en faire une caractéristique du vide, c'est l'interprétation énergétique de Λ. Dans la théorie quantique des champs, un vide de densité d'énergie ρ non nulle se traduit par une pression négative, une tension autrement dit, de même valeur (à un facteur c² près) et de signe opposé à la densité d'énergie.
P = -ρ.
C'est l'équation d'état du vide. Le signe de la gravité est donné par (ρ + 3P), et on voit qu'indubitablement c'est négatif pour un vide énergétique. Le vide gravite répulsivement. Or la TQC impose que l'état d'énergie du vide soit non nul. Ce qui nous sert sur un plateau la constante cosmologique et son interprétation physique, et fait le lien entre les deux grandes théories qui fondent toute la Physique.
Le lien entre la densité d'énergie et Λ est tel que :
ρc² = Λc4/(8πG)
Le "petit" soucis est que la valeur prédite par la TQC n'est pas du tout dans les clous en terme d'ordre de grandeurs par rapport à la valeur mesurée par la cosmologie.
Dans ce cas, ça revient à mettre Λ à droite de l'équation, du côté du le tenseur énergie-impulsion qui décrit le contenu (en énergie et impulsion) de l'espace-temps.
Rµν + 1/2 Rgµν = κTµν - Λgµν
C'est aujourd'hui l'interprétation dominante, d'où le terme d'énergie sombre qui est majoritairement utilisé pour désigner la cte cosmo responsable de l'accélération de l'univers.
Dernière modification par Gilgamesh ; 14/01/2023 à 19h58.
Parcours Etranges

Normalement avec un parcours un peu scientifique même ancien, tu aurais du avoir vu à un moment les différentielles et les intégrales ... même si tu as oublié. C'est un peu le minimum pour faire des calculs en science...(Réponse à Pachacamac bien sur pas à Gilgamesh !)
Dernière modification par Archi3 ; 14/01/2023 à 19h46.

@ les dérivées et les intégrales oui, les équations différentielles aussi, mais pas les différentielles me semble t'il. J'ai regardé le programme des TS spécialité math c'est pas au programme, j'ai regardé aussi ce lien que mach3 m'avait conseillé ci , d'une part c'est un peu compliqué (pour moi) et je ne me souviens pas les avoir rencontrées , d'autre part le primo posteur dit qu' on lui a introduit cette notion alors qu'il était en deuxième année d'une prépa intégrée dans une école d'ingénieur.
Dernière modification par pachacamac ; 14/01/2023 à 20h41.

Aussi tu parlais des expressions mathématiques et du comportement des intégrales nécessaires pour comprendre pourquoi l'expansion a d’abord décéléré puis s'est accéléré.
S'il suffit d'un peu de math je serai curieux de voir ça et ravi de plonger dans ces équations.

