là tu as tort. Aucun modèle n'est exact mais ça n'empêche pas de postuler une distribution de probabilité sur l'ensemble des modèles. C'est ce qu'on appelle l'approche bayesienne et si elle est parfois contestée elle n'en demeure pas moins mathématiquement valide.Envoyé par Archi3
ah bon alors quelle est cette distribution de probabilité quand il n'y a qu'un seul modèle disponible?
Il n'y a jamais qu'un seul modèle. Ce que tu appelles "un" modèle est en fait un ensemble de modèles, qui diffèrent les uns des autres par un certain nombre de paramètres. C'est sur ces paramètres qu'on postule une distribution. Si on a "plusieurs" modèles, c'est-à-dire finalement plusieurs classes de modèles qui dépendent de paramètres, on peut éventuellement postuler une loi de probabilité sur les classes de modèles et des distributions (conditionnelles donc) sur les paramètres. C'est ce que je fais couramment dans mon travail (sauf qu'il s'agit de modèles eux-mêmes probabilistes et qu'il s'agit de génétique des populations).
Déjà ce n'est pas pareil de parler de la distribution des paramètres d'un modèle et de différents modèles. Bien sur que si, on peut n'avoir qu'un modèle, il suffit que tu t'intéresses à un truc qui n'a jamais intéressé personne d'autre (par exemple expliquer le nombre de fourmis dans ta cuisine en fonction de la saison), que tu pondes un modèle pour le prédire, et tu n'en auras qu'un ! je te défie alors de calculer ou d'estimer un quelconque truc qui représente la "probabilité que ton modèle soit juste" - et qui ne serait surement pas 1 bien qu'il soit tout seul !
Meme chose pour la "distribution de probabilité de paramètres" qui n'existe pas plus. Ce que tu peux estimer, c'est la vraisemblance, c'est à dire la probabilité que tu estimes la réalité observée si ton modèle est supposé juste. Mais ce n'est pas une probabilité que ton modèle soit juste (qui est encore une fois zéro ...). Rien n'empêche par exemple la vraisemblance de deux modèles différents d'être de 90 %.
Dernière modification par Archi3 ; 08/10/2016 à 12h04.
Dans l'approche bayesienne, on postule une distribution sur l'ensemble des modèles. La question n'est pas de savoir si elle "existe", c'est un choix du modélisateur, ni plus ni moins. Compte tenu de ce choix, et compte tenu des observations, on peut calculer une loi de probabilité, dite a posteriori, sur l'ensemble des modèles. Cette loi peut servir à chosir un modèle. Maintenant, il peut arriver que plusieurs modèles aient la même (densité de) probabilité a posteriori et dans ce cas on ne peut pas les départager. Ca signifie, soit que le système n'est pas identifiable et dans ce cas il n'y a à peu près rien à faire, soit qu'on a besoin de plus d'observations.
encore une fois non , il n'y a pas de distribution de probabilité (au sens d'une mesure d'intégrale 1) sur l'ensemble des modèles, qu'elle soit bayesienne ou pas. Je t'ai donné un contre exemple trivial avec un seul modèle ou la seul distribution imaginable serait P=1, et encore une fois un modèle n'est qu'un modèle, c'est à dire ne vise jamais à être parfaitement exact, donc sa "probabilité" qu'il soit "juste" est simplement zéro.
d'ailleurs je te défie de trouver un seul article scientifique faisant ce genre de chose, et comme j'ai dit la référence donnée par Cotissois ne fait pas du tout ça.
j'aurais du mal à n'en trouver qu'un mais on doit pouvoir en trouver mille sans difficulté. Bon j'arrête de discuter ce point, je commence à penser que tu es de mauvaise foi et je vais m'énerver.
la meilleure façon que tu aurais de prouver ma mauvaise foi, c'est d'en trouver un justement ... (je ne pas demandé de n'en trouver qu'un !)
sur d'autres sujet que le climat, penses tu par exemple qu'on ait calculé une probabilité que la théorie des cordes ou de la matière noire soit juste ? si ça existe, j'aimerais bien connaitre sa valeur !!
Il y a un chapitre entier du dernier rapport du GIEC sur l'évaluation des modèles. Ca serait bien si on partait de là. Ca éviterait de discuter dans le vide.
Dix secondes pour écrire une bêtise, parfois des heures pour montrer à tous que c'en est une...
La validation ds modèles ne semble pas du tout se faire en calculant je ne sais quellle distribution de probabilités de je ne sais pas au juste quoi.
Par contre, toute une stratégie est mise en oeuvre qui vaut sans doute la peine de s'y attarder un peu
Dans le résumé du chapitre, on peut lire ceci
Que je traduisIn this chapter,
model evaluation covers simulation of the mean climate, of historical
climate change, of variability on multiple time scales and of regional
modes of variability. This evaluation is based on recent internationally
coordinated model experiments, including simulations of historic and
paleo climate, specialized experiments designed to provide insight into
key climate processes and feedbacks and regional climate downscaling.
Dans ce chapitre l'évaluation des modèles couvre les simulations du climat présent, de l'historique des changements climatiques , de la variabilité aux différentes échelles de temps et des modes régionaux de variabilité. Cette évaluation est basée sur des expériences numériques coordonnées internationalement incluant des simulations historiques et paléoclimatiques, des expériences spécialisées destinées à investiguer des processus climatiques clés et les rétroactions ainsi que des des expériences de réduction d'échelle du climat global au climat régional (je n'arrive pas à traduire "downscaling" plus simplement , il doit bien y avoir plus concis je suis preneur , mais on a progressé, merci )
Dernière modification par yves25 ; 08/10/2016 à 15h53.
Dix secondes pour écrire une bêtise, parfois des heures pour montrer à tous que c'en est une...
"Downscaling": réduction d'échelle ?
N'a de convictions que celui qui n'a rien approfondi (Cioran)
Plus concis que "vers" c'est difficileTa traduction est bien mais je mettrais "jusqu'à" à la place de vers. Il est difficile sans faire lourd de traduire la nuance apportée par "down" ou alors "depuis... en descendant jusqu'à l'échelle..." mais est-ce que cela apporte quelque chose de plus ?
Rien ne sert de penser, il faut réfléchir avant - Pierre Dac
C'est en tout cas cohérent avec cette définition (où les statistiques pointent leur nez).
N'a de convictions que celui qui n'a rien approfondi (Cioran)
Oui, merci .i c'est nettement mieux mais reste à dire de quelles échelles on parle. J'ai modifié en conséquence.
Dernière modification par yves25 ; 08/10/2016 à 15h53.
Dix secondes pour écrire une bêtise, parfois des heures pour montrer à tous que c'en est une...
Oui, la définition st bien nécessaire en fait quant aux statistiques, ça n'a rien à voir avec celles d'Archi qui correspondent à ...je ne sais toujours pas quoi... mais il paraît que je ne comprends rien
Dix secondes pour écrire une bêtise, parfois des heures pour montrer à tous que c'en est une...
[hors sujet]Sauf que downscaling est ici un participe présent et non un substantif [/hors sujet]
Rien ne sert de penser, il faut réfléchir avant - Pierre Dac
Je ne sais pas trop ce que tu appelles "mes" statistiques alors que je disais seulement que les "distributions de probabilité" des modèles, ça n'existait pas, contrairement à ce que disait minushabens. Ce qui ne veux évidemment pas dire qu'il n'existe pas d'évaluation de leur qualité ...
Justement à propos des prédictions locales et du "downscaling", un article assez stupéfiant publié ici :
http://journals.ametsoc.org/doi/full...S-D-13-00255.1
et dont un compte rendu est ici :
http://www2.ucar.edu/atmosnews/persp...te-variability
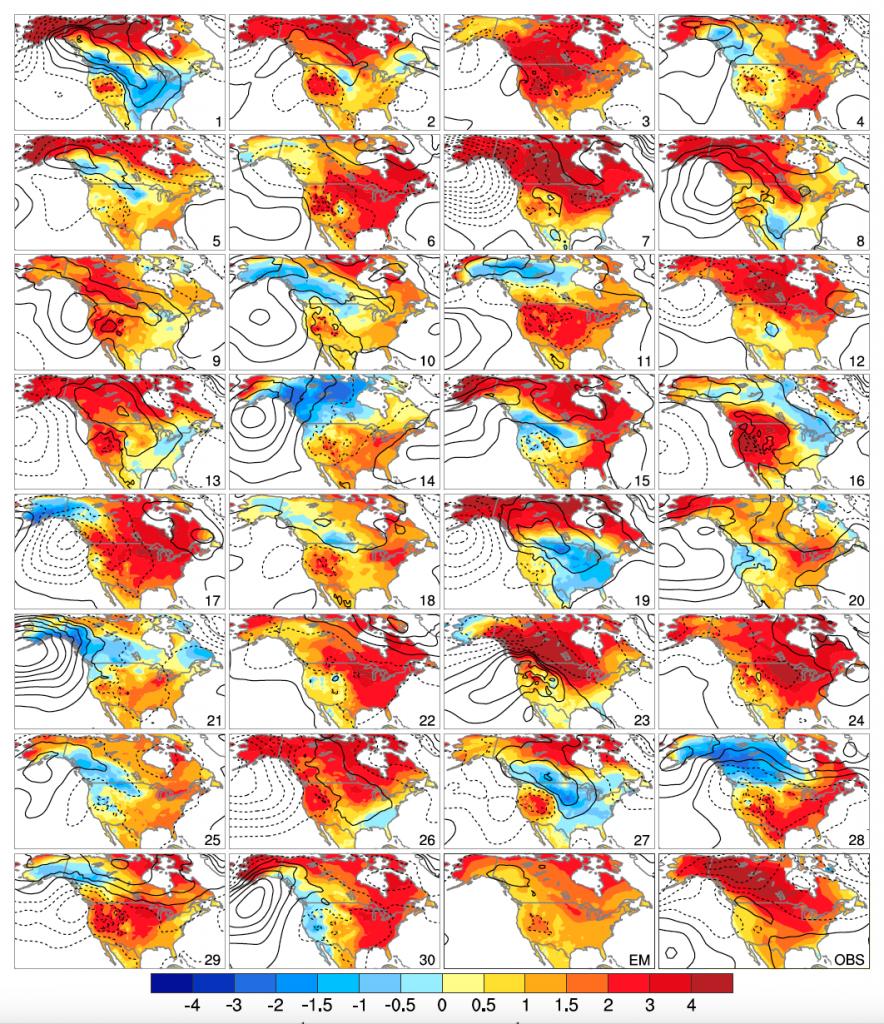
les auteurs ont réalisé 40 simulations avec le même modèle en changeant très légèrement les conditions initiales, de 1920 à 2100, en changeant la température de moins d'un "trillionieme" (millième de milliardième en bon français) de °C. La figure reproduit les pentes observées localement (pas globalement) sur l'Amérique du Nord, et elles sont très différentes selon les runs ! bref les prédictions locales sont dominées par le caractère stochastique du climat, ce qui a mon sens empêche toute prédiction locale sensée? à moins que le vrai climat ne soit plus déterministe que les modèles, mais alors ça veut dire qu'on ne peut pas non plus utiliser les modèles actuels pour des prédictions locales.
Merci pour le lien, c'est une étude assurément intéressante.
Elle dit que dans un état thermodynamique global légèrement différent, le système climatique répond peut-être par une organisation sensiblement différente.
Peut-être. Il faut bien voir que ce n'est pas le système climatique qui est testé, mais le modèle.
Pour moi c'est comme dire qu'on sait pas à quelle heure il va neiger... cela n'empêche pas de savoir que ce sera plus probablement en hiver. Surtout, on le savait déjà, que les variations locales sont beaucoup plus difficiles à prédire que les variations globales. Bref, je ne vois pas quelle est l'information nouvelle ou intéressante dans cet article. Pourrais-tu expliquer ce que tu y vois?
Dernière modification par Jiav ; 10/10/2016 à 19h20.
ce qui n'était pas évident, c'est que le RC moyen local soit inférieur à la variabilité naturelle (ce qui est possible même si la moyenne globale est supérieure à la variabilité naturelle puisqu'on moyenne sur de nombreuses régions pour prendre la moyenne). Mais pour les conséquences humaines, elles sont plutot due à la variation locale , après tout, tu te fiches quand tu habites dans une région de la moyenne mondiale non?
Que tu te fiches de ce qui arrive à des "étrangers à ta région", je crains de ne pas en douter.
Mais ton raisonnement est foireux même en dehors de toute considération éthique: autant jouer à la roulette russe avec 5 amis, sur le prétexte qu'on se moque de la moyenne des dégâts. Cela te fera comme même une chance sur six de jamais comprendre ton erreur de raisonnement.
Bravo pour la méthode de l'épouvantail, je n'ai pas écrit que je me fichais des "étrangers à [ma] région" (bizarre de mettre des guillemets à ce qui n'est pas une citation), mais de "la moyenne mondiale" : il n'y a pas de raison de penser que les étrangers à la région vivent autre chose que toi , c'est à dire une variabilité dominée par la part chaotique du climat.
Quant à la roulette russe, c'est une comparaison foireuse, puisque justement elle introduit une espérance mathématique de décès bien supérieure à la variabilité naturelle, ce qui est exactement l'inverse du cas étudié ici.
Ok, ton raisonnement est toujours "surprenant", mais il n'a pas la connotation xénophobe que j'y avais vue. Mes excuses donc. (pour l'usage des guillemets, voir ici)
Ton raisonnement demeure "surprenant" car:
1) parmi les impacts les plus importants du réchauffement, il y a la montée du niveau des océans et leur acidification, deux phénomènes pour lesquels la variabilité locale n'a aucun impact. Il est improbable que tu l'ignores.
2) les modèles n'ont jamais été construits pour être précis concernant les variations locales. Si les modèles font une erreur e1 sur la température globale, il est très probable qu'ils feront une erreur e2>>e1 sur les variations locales. Ton raisonnement tient e2 pour parole d'évangile, alors que tu dénigre régulièrement e1. Cela se peut que tu l'ignores, mais il est difficile d'y voir un raisonnement objectif.
A l'échelle globale, la variabilité reste forte quand même comme le montre la figure jointe mais elle se réduit notablement quand on calcule les tendances sur 20 ans au lieu de 10.
Le climat simulé par ce modèle semble fort chaotique, ça serait à vérifier avec d'autres modèles mais l'exercice mobilise des moyens gigantesques. Faut pas trop rêver dans l'immédiat.
La situation est similaire à ce qui se passe en météo et c'est pour cette raison que les simulations d'ensemble sont plutôt plus fiables sur l'échéance à long terme.
Les tendances globales sur 20 ans sont assez resserrées , non?
A noter qu'il s'agit de la RCP 8.5. Le forçage est donc fort et il l'emporte largement sur la variabilité décennale générée par ce modèle.
Dernière modification par yves25 ; 11/10/2016 à 18h07.
Dix secondes pour écrire une bêtise, parfois des heures pour montrer à tous que c'en est une...
Sur cette étude, j'ai fait mon résumé, mais je ne comprends pas trop la conclusion des auteurs. La variabilité naturelle ne se juge pas par un modèle déterministe.
En météorologie, l'exercice de deux prévisions légèrement différentes sur l'état initial est une mesure de la prévisibilité liée à la seule incertitude des conditions initiales. L'effet papillon qui se produit vient de la forme mathématique des équations. On ne juge pas du fonctionnement réel de la Nature, c'est juste qu'il y a mauvaise prévisibilité pour celui qui a une méthode déterministe.
Pour le climat, il n'y a pas d'incertitude sur les conditions initiales puisqu'on a une longue fenêtre de calibration avant de passer en mode déterministe. Du coup, l'exercice de deux prévisions légèrement différentes traduit la sensibilité des équations à des perturbations qui n'existent pas. Néanmoins, cela permet de réaliser à quel point le modèle déterministe est chaotique et pourquoi il faut être au point sur la calibration initiale. Ce n'est pas révolutionnaire mais c'est pédagogique.
La variabilité naturelle se juge elle uniquement par l'historique. Les prévisions climatiques ont une variabilité naturelle simulée. Cela permet de réaliser ce qui est possible, mais cela ne dit pas ce qui se passera. Néanmoins, le principe de précaution, qui est la doctrine à l'origine du GIEC et de la CNUCC, a besoin de simuler une variabilité naturelle pour savoir ce qui est possible.
Que veux tu dire?Sur cette étude, j'ai fait mon résumé
Ils ne prétendent pas avoir estimé la variabilité du climat mais bien celle de leur modèle. Leur conclusion est plutôt celle cimais je ne comprends pas trop la conclusion des auteurs. La variabilité naturelle ne se juge pas par un modèle déterministe.
We anticipate analysis of this ensemble, alone or in combination with other ensembles and/or regional climate simulations, will lead to novel and practical results that will inspire probabilistic thinking and inform planning for climate change and climate model development for many years to come.Ce n'est pas clair, en tout cas pour moi. Cette variabilité simulée donne une idée de la variabilité dans les projections mais ça n'empêche en rien que la moyenne d'ensemble (surtout la moyenne d'ensemble d'un modèle ) ne puisse pas être crédible comme l'est la moyenne d'ensemble d'un modèle météo.Les prévisions climatiques ont une variabilité naturelle simulée. Cela permet de réaliser ce qui est possible, mais cela ne dit pas ce qui se passera
Dix secondes pour écrire une bêtise, parfois des heures pour montrer à tous que c'en est une...
Très improbable. On le voit souvent invoqué pour la météo, mais en réalité l'effet papillon (l'augmentation des écarts de prédiction à partir d'écarts initialement faibles) est une caractéristique des modèles déterministes avec un faible nombre de dimension (i.e. comme ceux proposés par Lorentz dans les années 70). Quand on augmente le nombre de dimension (i.e. les modèles actuels), les effets chaotiques disparaissent et deviennent rapidement indiscernables d'un bruit stochastique. En fait on peut le voir avec les figures présentées par Yves: si le modèle était chaotique, on devrait avoir une variance sur 20 ans égale ou plus grande que la variance à 10 ans. Au contraire on voit une réduction, ce qui est un effet de moyennage typique des modèles stochastiques. On pourrait toujours imaginer qu'il y a un effet chaotique sur 10 ans, puis un moyennage, mais c'est improbable juste avec l'information que c'est modèle détaillé, donc avec un grand nombre de dimensions.
pour ce qui est de la montée des eaux, elle est toujours de 3mm par an donc 30 cm par siècle : les extrapolations très supérieures proviennent de modèles hasardeux non confirmés par l'expérience (et qui si ils étaient vrais impliqueraient qu'on ne peut pas vraiment l'éviter de touts façons).
Quant à l'acidification, elle n'est pas due au réchauffement mais au pouvoir acide du CO2, qui n'a rien à voir avec son absorption dans l'IR, mais c'est un détail... : elle n'a rien à voir avec les modèles climatiques de toutes façons, dont il est question sur ce fil.
tu penses bien que ce n'est pas par plaisir que les modèles ne sont pas précis, si ils pouvaient l'être pour les variations locales on ne s'en priverait pas. Je ne sais pas ce que tu appelles "dénigrer" e1, je n'ai fait que comparer des modèles aux observations : c'est inacceptable selon toi ?2) les modèles n'ont jamais été construits pour être précis concernant les variations locales. Si les modèles font une erreur e1 sur la température globale, il est très probable qu'ils feront une erreur e2>>e1 sur les variations locales. Ton raisonnement tient e2 pour parole d'évangile, alors que tu dénigre régulièrement e1. Cela se peut que tu l'ignores, mais il est difficile d'y voir un raisonnement objectif.
pour ce qui est d'y voir un manque d'objectivité, je te retourne le compliment ...;
