De la source du shell_theorem de Newton

[Ladrix]

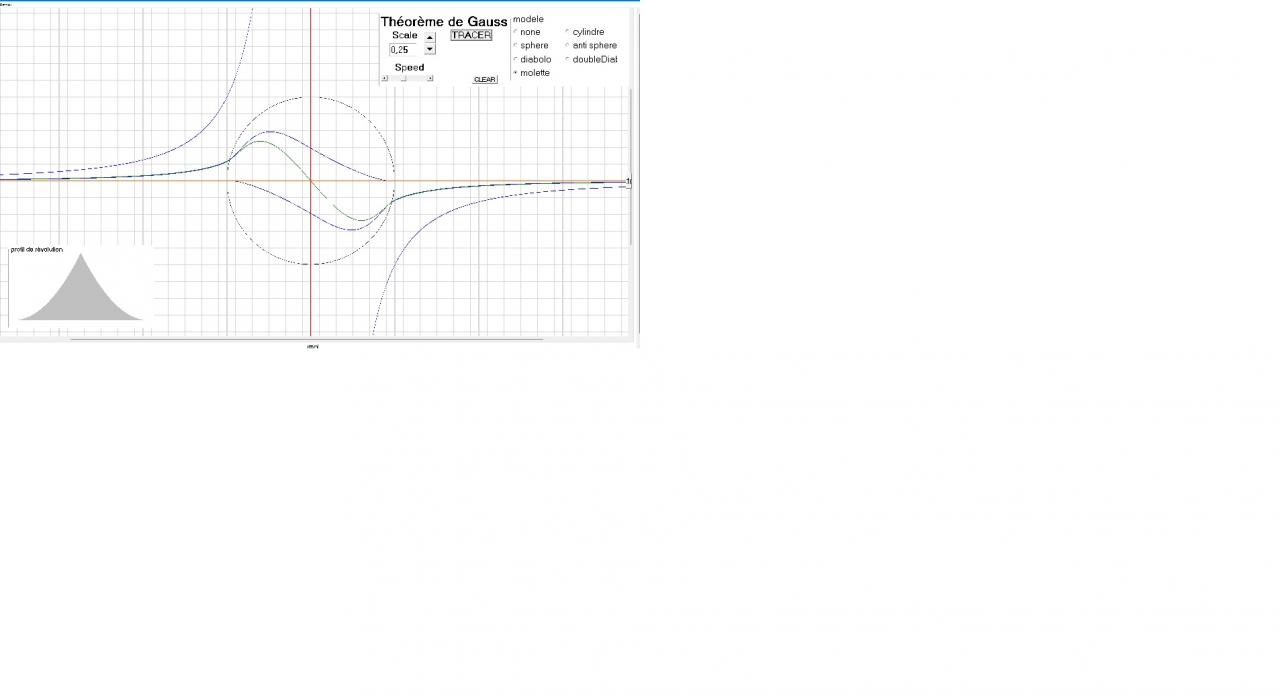
@gts2

Je n'ai pas de problème numérique.
Vous disiez faux pour mes calculs. bon, c'est surement vrai dans l'absolu.
Mais il suffit d'augmenter la finesse du découpage, c'est juste plus long à calculer.

Le théorème de la Gravitation de Gauss dont je dispose s'appuie sur des affirmations comme
La partie sphère extérieure projette le flux vers l'extérieur.
La sphère intérieure génère le flux depuis le centre.
Si la sphère intérieure est vide, il n'y a pas de flux de ce fait, donc le flux interne total est nul.
C'est ce que j'ai cru comprendre.
En fait c'est exact et mon tracé dans "Newton versus Gauss un grand écart négligé ?" #22 est conforme à la conclusion de Gauss. mes calculs consistent en l'intégration numérique conséquente de mx/((x²+y²) (x²+y²)^1/2 sur une base de 4 E9 éléments sur 1E4 positions. soit 4 E13 calculs successifs de la fonction de Newton. (faut un bon algo pour ne pas mourrir de vieillesse avant la fin du calcul)
Mais la causalité de cette curiosité, elle est établie par mes soins en #27 qui traite d'une sphère pleine, mais la même méthode s'applique à la coquille vide et donne le même résultat. somme de la calote sphérique qui accélère et de celle qui freine. Cad la loi développée de Newton f(x) = mx/((x²+y²) (x²+y²)^1/2
(Newton +Pythagore + Thalès )
Pour inside et outside je vous remercie pour cette fonction compactée mais je la retrouve pas sans la page Wiki et pas plus dans les Principia, mais je suis peut être trop expéditif dans mes recherches textuelles...
Comme cet intermède inside outside me semble bouclé (sic) je m'arrêterai là.

Merci encore Gts2 pour vos contributions.

Ladrix
-----

[Archi3]

Bonjour à tous


@Archi3

Pas toutes mais j'ai des projets...

Le Shell_theorem ne traite pas de physique du moins les fonctions Inside et Outside mais d'une correction purement calculatoire de la loi initiale de Newton.
Ces fonctions sont bizarres et non justifiées préalablement. (il me semble)
La inside est différente de la outside par son calcul des limites, why ?
Peut on condenser ces deux recettes en une seule ? je ne sais pas encore.
La confiance n'empêche pas le contrôle.

"contrôle" ? tu veux dire que si on a démontré un résultat analytiquement, et que tu fais un calcul numérique qui n'est pas en accord, tu en déduis que c'est le résultat analytique qui est faux et le calcul numérique qui est juste ?

[Ladrix]

@Archi3
je n'ai pas d'a priori.
Si l'écart indique que les deux approches sont en opposition, ou très éloignées la question qui se pose est
Laquelle des deux s'éloigne le plus du réel (seul critère)
Il reste la réponse que les deux seraient fausses.
Donc une enquête s'impose en oubliant les arguments d'autorité.
Enquête consistant à essayer d'établir la généalogie des deux approches .
Un concept plus juste avec des calculs faux ou un concept plus faux avec des calculs justes.
Je considère par principe que les calculs des Mathématiciens sont justes.

Sur les a-priori

dans mon étude de la gravitation je retouve la fonction développée de Newton.
je trace quelques courbes de celle-ci.
C'est beau, galbé, magnifique. un vrai Physicien consulté me déclare c'est cool ton truc.
Dans mon idée (a-priori) quand j'aurai établi un calcul de mes 4 E9 éléments sur 1E4 points de parcours, je vais obtenir une belle courbe galbée etc.. en rapport avec les tracés initiaux.

Ce fut ouvrageux mais très enrichissant, m'obligeant à me remettre à Delphi 7 après des année d'abstinence.
En effet c'est si je ne m'abuse une intégrale triple, ce qui est pour moi un monde magique...
Je trace le résultat : patatras : c'est la courbe de Newton 1/x² mâtinée Gauss en interne de l'attracteur avec angle vif, très vif horriblement vif en x= 1 et x=-1
Après une petite déprime, c'est le résultat exact à l'approximation près du dx et dy de mes intégrations numériques. (1/1000 du rayon de l'attracteur)
Donc, l'a-priori, moteur de l'effort, doit être oublié au résultat final.
Si l'approche analytique est exacte, les deux méthodes doivent se recouper, le numérique par contre à l'avantage de pouvoir être utilisé pour des variantes de forme par exemple sans contorsions, juste à introduire les valeurs initiales comme le profil de révolution de l'objet étudié.
Cf ma courbe profil baptisé molette (je manque de romantisme)

impossible à obtenir en anlytique, il me semble.

la courbe centrale est l'accélération gravitationelle globale qui n'est pas une droite comme dans la sphère.(Gauss précise cette exception)
la bosse vers le haut ce qui accélère
la bosse vers le bas ce qui freine
en repère externe le 1/x² suivi du -1/x²
J'en déduit la causalité des écarts avec le 1/x² initial .
note sur ce tracé je n'ai pas fait la normalisation à masse constante avec une sphère de rayon 1.(les valeurs scalaires m'indiffèrent à ce point de mon étude)


Ladrix

Ps
Les imperfection de l'image sont dues à une réduction de la copie d'écran par Paint.exe

Note
mon exécutable ne pèse que 1.9 Mo
nécessite 100 Mo de Ram à l'éxécution.
zut, l'image est réduite mais entouré de vide...

[Archi3]

@Archi3
je n'ai pas d'a priori.
Si l'écart indique que les deux approches sont en opposition, ou très éloignées la question qui se pose est
Laquelle des deux s'éloigne le plus du réel (seul critère)
Il reste la réponse que les deux seraient fausses.

donc tu penses qu'une démonstration analytique reposant sur des mathématiques prouvées "pourrait" être fausse ?
qu'on s'entende bien , il se pourrait que la gravité ne soit pas en M/r^2 (d'ailleurs en RG c'est le cas). Mais une fois qu'on postule qu'elle est en M/r^2, le Shell theorem en est une conséquence rigoureuse et incontestable suivant les principes mathématiques. Donc si tu penses qu'il se "pourrait" qu'il soit faux, ça signifie que tu ne fais pas confiance aux principes mathématiques ?

[MissJenny]

je n'ai pas d'a priori.

je suis d'accord avec Archi3. Autant confronter un résultat théorique aux mesures expérimentales a du sens, pusiqu'il est toujours possible que les hypothèses de départ soient erronées, ou qu'un phénomène inconnu intervienne, autant vouloir valider par le calcul un résultat prouvé mathématiquement n'a aucun sens.

Si l'écart indique que les deux approches sont en opposition, ou très éloignées la question qui se pose est
Laquelle des deux s'éloigne le plus du réel (seul critère)

ça va être dur de trouver dans le monde réel une sphère parfaite d'épaisseur nulle et avec aucune autre masse à proximité...

[Ladrix]

@Archi3

Vos affirmations ne sont pas fondées.
Je ne pense rien.

Les mathématiques sont des règles qui régissent les rapports quantitatifs des données collectées par l'expérience.
Elles sont par définition exactes.

Mais une fois qu'on postule qu'elle est en M/r^2

Exact Newtonl le postule et il a raison.
Mais ce postulat est avec une limite qu'il exprime toujours.
Cette fonction n'est exacte que si on peut considérer l'attracteur ponctuel.
Tant que c'est le cas la fonction en 1/x² est exacte.
Mais le Théorème de Gauss nous dit :
Yes mais à l'intérieur de l'attracteur que nenni, c'est x.
Why m'écriais-je dans ma baignoire !!!

Because je réponds ici avec ma courbe de coquille commentée (non c'est l'attracteur plein qui est commenté)
Mais le comment du plein est valide pour le comment du vide.

@MissJenny
La preuve du pudding c'est qu'on le mange.
Le phénomène qui déforme la courbe en x² de loin est la courbe en 1/x² de Newton, il n'y a aucune autre cause que la dispersion sur l'axe x, y et z d'une masse qui n'est pas ponctuelle.
reste à savoir la causalité de la loi 1/x² . Mais c'est inutile la question es tobsolete

il se pourrait que la gravité ne soit pas en M/r^2 (d'ailleurs en RG c'est le cas)

Bonne journée à tous.

Ladrix

Ps
admirez et commentez ma courbe #33
j'en ai d'autres encore plus belles.
Mon algo est conforme aux règles mathématiques.

A noter
Puisqu'on me chipote que l'intégration que je fait numériquement serait imprécise, c'est exact c'est la plus simple:celle par rectangles faite à la volée.
Je l'ai utilisée car mon travail est heuristique, l'exactitude scalaire n'est pas mon but initial. et avant de fignoler faut vérifier que c'est utile.
Mais, qu'a celà ne tienne, je vais prendre un rayon (je suis en coordonnée forestières : cernes en tranches ) multiple de 3 et faire mes intégrations par groupe de 3 points par la méthode de Simpson. J'ai ressorti mon Quinet pour l'occasion.
Je pourrai régresser de 1000 à 999 dx, dy par rayon (je n'ai pas de dz), que nenni, je vais passer à 3000.
Le temps de calcul passra de instantané à un petit clignement des yeux,
Pour le calcul du champ initial (ma base de données 1,2 E7 points => 1.08 E8 points ) je vais passer de 50 ms à 500 ms,
Pour établir la courbe de chaque profil en scannant ma BD, 3 fois très court ça reste pas grand chose.
Mais c'est la ram qui va être juste il m'en faut 1+ Go et W11 est envahissant, je vais devoir le renvoyer dans ses cordes, si je me remémore mes actions salvatrices sur XP du temps jadis. ( si je ne détruit pas W11...)

La solution serait de passer d'une tablette Microsoft Go3 4Go à la même en 8Go, 650 euros, tout réinstaller, j'hésite.

[mtheory]

@Mthéorie
Il n'est pas possible d'accéder au livre de Chandrasekar :
DOWNLOAD OPTIONS
No suitable files to display here.
14 day loan required to access PDF files.

Bien sûr que si, on peut le lire en ligne, je n'ai jamais dit qu'il était téléchargeable sur ce site, il existe en piraté ailleurs mais je ne vais évidemment pas poster le lien, c'est illégal et je ne le donnerai pas non plus en MP.

[Ladrix]

@MTheory

De toutes façon je n'arrive pas à lire un bouquin sur un écran.
il y a 10 pages accessibles dont les pages de garde.

je viens de recevoir la version papier Bernard Cohen et Anne Whitman (University of California Press)
C'est déjà pas mal.

Après je verrai pour le livre de Chandrasekar (le jour du chèque de la retraite je serai peut être moins radin)

Merci encore

Ladrix

[ArchoZaure]

Le mieux à ce stade ce serait de pouvoir jeter un œil sur le code qui produit "l'intégration" (si j'ai bien compris).
Sachant qu'il est facile de se tromper, et pas seulement d'un point de vue informatique, aussi du point de vue mathématique, lorsqu'il s'agit d'ajouter des petites parties permettant de reformer le tout.
Par exemple je me souviens vaguement d'une démonstration qui permet de donner une valeur erronée de la circonférence du cercle à partir d'une mauvaise intégration (pas de problème de code donc ici mais d'algorithme).
Aussi, ajouter des petites sphères est-il l'équivalent d'ajouter des petits points ?....par exemple.

A l'examen du code on sera fixé.

[Ladrix]

@ArchoZaure
vous communiquer mon code.
Oui, bonne idée
Dès que vous aurez publié une ébauche de vos propres travaux.
Merci de nous faire admirer quelques courbes de votre crû.
En effet vous devez exciper de vos qualités pour pouvoir prétendre juger des travaux des autres .
J'ai une Vcard.
Vous avez des références ?

Les miennes sur Futura présentement :
Courbes produite pour une sphère pleine,
courbe produite pour une coquille vide,
Autre courbes suivant profils de révolution,
Causalité de l'anomalie du théorème de Gauss sur la loi F(d) =GMm/d² .
Anomalie énorme qui ne fait moufter personne depuis plus de deux siècles.

éléments communiqués :
La fonction de Newton développée : f(x) = mx/(x²+y²)^3/2
codée en xy/(x²+y²)(x²+y²)^1/2
Calculs sur un système de coordonnées cylindriques (cernes du bois coupé en tranches) projetées en xy éliminant ainsi l'axe z
intégration de base par la méthode des rectangles.
Explications de ma méthode algorithmique.
Les résultats sont conformes aux différents théorèmes à l'exception du dogme 1/x² pour un attracteur non ponctuel. Dogme rejeté par l'auteur de la loi : un certain Isaac Newton...

Note .je ne traite pas avec des ennemis déclarés comme tels. fin de note

J'insiste sur le fait que je ne professe aucune loi différente de celle de Newton, loi que je ne fait qu'appliquer avec la plus grande rigueur. Ce qui agace il me semble.

Dans l'attente fébrile de vous lire,

Ladrix.

note
A propos de pi
avez vous considéré les implications de la longueur de Planck sur la valeur de pi ?
Moi si. Texte sur demande par Mail. MDR
Pour les épicycles c'est une vieille affaire qui a aujourd'hui une très forte cote. autre texte, même remarque.

[Archi3]

@Archi3

Vos affirmations ne sont pas fondées.
Je ne pense rien.

Les mathématiques sont des règles qui régissent les rapports quantitatifs des données collectées par l'expérience.
Elles sont par définition exactes.

du coup si le résultat de ton calcul numérique ne correspond pas aux résultats des mathématiques "exactes par définition", quelle serait ta conclusion ?

[JPL]

Merci de nous faire admirer quelques courbes de votre crû.
En effet vous devez exciper de vos qualités pour pouvoir prétendre juger des travaux des autres .

Et ton code, c’est le tout de ton cru ?

[Ladrix]

@Mach3

du coup si le résultat de ton calcul numérique ne correspond pas aux résultats des mathématiques "exactes par définition", quelle serait ta conclusion

Bonjour Mach3.
Le calcul numérique est forcément l'approximation d'une approche mathématique puisqu'elle l'utilise sur des petits éléments en grand nombre.
C'est ce que je fais : j'applique Newton à Newton.
Si ça correspond vraiment pas, j'ai répondu plus haut à cette éventualité.
J'ai même précisé que mes calculs n'ont pas donné le résultat que j'avais anticipé.
Je me répète.
si le concept traité par méthode analytique est proche du réel son calcul est a eu près exact puisque les règles mathématiques sont rigoureuses. Cas d'un cercle, d'une sphère homogène et isotrope entourée de vide qui ne perturbe pas l'équation. Mais ça n'existe pas.

Si un calcul approché par éléments finis donne un resultat très différent des prévisons analytiques alors la question de pose : le calcul de l'ingénieur est-il faux, ou le concept de base du mathématicien est il erroné.
La réalité tranche.
Calculé par éléments finis suivant des règles mathématiques rigoureuses, l'avion vole correctement, il ne se casse pas dans les limites prévues par un calcul effectivement approximatif . Il en est fabriqué 5000 une affaire en or. En plus on a gagné la guerre. On affinera la méthode pour les contrats suivants.
L'avion du mathématicien lui, ne volera jamais car la fonction rigoureuse qui va le déterminer intégralement (sic) est impossible à établir.
Aucun Mathématicien ne s'y collera de toutes façons.
un petit Smiley

Ladrix

[Ladrix]

@Jpl

L'affaire se corse.
j'aime l'approche en douceur...

c'est bien le trou de mon crû.
Je code en Delphi 7.
Ma technique en tout est d'éviter les choses inutiles comme recalculer 1E9 fois une fonction avec les mêmes données.

Pourquoi cette insidieuse question ?
vous avez fait la même chose ?
Je calcule comme je l'ai précisé .
4E9 éléments sur 1E4 positions en beaucoup moins d'une seconde. ma bd de champ gravitationnel 1.2 E7 points est générée en 50ms (à mon grand étonnement)
Ces courbes je les ai postées ici.
On m'objectera qu'un Pc a 420 euros ne peux pas effectuer tout ces milliards d'opérations dans le temps annoncé. 50 ms total à 5 ns par boucle.
c'est exact. c'est impensable.
Mais le résultat est là.
J'ai expliqué mon algo.
coordonnées forestières cernes découpées en tranches 1000 cernes 1000 tranches au rayon.
Tous les éléments d'une même cerne ont les mêmes paramètres on gagne *500 pour 1000 cernes. en éliminant l'axe z.
au lieu de calculer 1000 fois par rayons la translation de la sphère de 4 E9 éléments on calcule les valeurs d'un cylindre conteneur de toute la couse prévue, sur 10 rayons 12 000 calculs de 4 E9 on en fait au total que 12 E7 points de champ.
cette base de données il suffit alors de la scanner avec le profil etudié soit 2000 lectures et additions par position du trajet de l'attracté. C'est diabolique de rapidité.
Je suis obligé de mettre une tempo pour voir la courbe se générer.
Je peux du coup scanner n'importe quel profil, et avec 2 courbes les profils creux, ou de densité différentes, de quoi remplir des annuaires de très beaux tracés.
J'ai posté le résultat ici. Je n'ai pas tracé mes courbes avec un perroquet et un rötring...
Comme les courbes de sphères vide et pleine sont conformes aux attentes (jamais tracées par ailleurs il me semble) je considère qu'elles sont innataquables à moins de contester Newton et Gauss.

Ladrix.

Je vous comuniquerai des parties de mon code sous peu, le temps de les extraire de mes listings.
A cette heure je vais dormir.

Bonne soirée à vous.

[Archi3]

Si un calcul approché par éléments finis donne un resultat très différent des prévisons analytiques alors la question de pose : le calcul de l'ingénieur est-il faux, ou le concept de base du mathématicien est il erroné.
La réalité tranche.

c'est bien cette question là que j'essaie d'éclaircir dans ta démarche : pour toi, les deux possibilités sont ouvertes, comme quand tu vois débattre deux personnes qui sont en désaccord sur un sujet que tu ne connais pas ?

[Archi3]

Pour préciser "le concept de base ", en l'occurrence, c'est la théorie de l'intégration qui est précisément la théorie qui calcule la limite d'un calcul en éléments finis lorsque tu fais tendre le nombre d'éléments vers l"infini, et leur taille vers zéro.

quand tu fais un calcul avec un très grand nombre d'éléments, tu DOIS (selon cette théorie) trouver un résultat très proche du résultat analytique., sachant que l'intégration finie étant toujours une approximation du résultat analytique, c'est toujours le calcul fini qui est moins précis que la limite théorique.

Si ce n'est pas le cas, et que tu observes des différences significatives, bien plus importantes que ce qui est attendu de la discrétisation, il ne reste que deux possibilités logiques :

a) tu t'es planté dans ton calcul numérique

b) la théorie de l'intégration, qui est démontrée depuis des siècles, qui est utilisée par tous les scientifiques , par exemple ceux qui arrivent à construire des accélérateurs de particules géants qui fonctionnent ou faire atterrir des robots sur des comètes à des centaines de millions de km, serait fausse

donnes tu des probabilités relatives similaires à ces deux hypothèses, ou l'une te parait a priori bien plus probable que l'autre si tu observes une différence significative entre la théorie et le résultat de ton calcul ?

[Ladrix]

Bonjour à tous.

@Archi3 #45
Réveillé par la teuf de mes colocs (des campagnols charmants) je réponds au saut du lit.

Je vais donc me re répéter.

Déjà, les discussions entre gens sur un sujet auquel je ne connais rien me laissent de marbre.
exemple : tout ce qui est chimie, qu'elle soit minérale ou organique.
Dans ce domaine mes limites sont
acide +base = sel +eau.
et
C'est la science des mises en commun des électrons de la dernière couche.

Pour tout un tas de sujets, je ne suis pas intéressé. Exemple récent : différence entre vide et Néant. J'ai bu du petit lait (fermenté)

Pour certains (sujets) je suis passionné.
Concernant ma démarche en Physique.
Je suis Matérialiste stricte (philo)
ainsi toute explication magique est exclue.
Exemple : pas d'exemple ##################.

Si, un exemple qui fera, je pense, consensus.

Le Janus de Petit.
Pas parce que le concepteur aura crû aux extra-terrestres, tout ado, j'y croyais. Je suis certain encore de leur existance (avec des réserves)
Mais parce que la spéculation effrénée même appuyée sur un corpus mathématique reconnu par l'ensemble des Physiciens, j'entend les Docteurs et Doctorants, est du domaine de l'incantation et n'apporte rien à la Science.

Dans le même genre, les théories des Branes qui repoussent l'inconnaissable de l'origine de l'Univers en en imaginant deux autres (inconnaissables ontologiques) dont l'interférence serait notre origine.
Pour le reste : la conservation absolue de l'énergie est un critère de choix entre deux débatteurs. Celui qui la rejette ou en tolère la violation est, à mes yeux celui qui à tort.
Bien sûr, celui qui la respecte peut aussi être dans l'erreur, pour d'autres raisons.

@Archi3 #46
Qui parle de Théorie de l'Intégration. Pas moi.
C'est un outil mathématique qui manie avec brio l'addition.

Quand je calcule une intégration numérique en traitant des bonnes données avec la bonne loi qui gouverne le phénomène, mon résultat est conforme à la même intégration des analystes des mêmes données avec les mêmes lois.
En cas d'écart significatif, il convient, dans tous les cas, de vérifier que les données traitées par les deux méthodes sont les mêmes ainsi que les lois appliquées pour le traitement. Si l'identité est confirmée et que les écarts sont maintenus, l'examen fenêtre tranchera.
Celui dont l'avion tombe à perdu. D'entrée je vous déclare : je ne monterai pas dans l'avion de l'un d'eux.

Il conviendra de contrôler la méthode par éléments finis par des points repères calculables analytiquement. C'est ce que j'ai exposé dans mon étude succinte de la recette Outside du Shell_theorem.
J'en avais fait de même pour mon exécutable sous Delphi à titre préalable.
Concernant des écarts que mes calculs etc... je me permet de renvoyer à mes quelques courbes ornant mes files ici-même.
Je n'ai pas eu le plaisir de voir tracée la courbe en 1/x² intégrée suivant les règles ds Mathématiciens qui nous montrerait l'exactitude du théorème de Gauss sur les coquilles vides, et du cas usuel des attracteurs pleins, et des intermédiaires plus ou moins épais.
Je rappelle pour les lecteurs intéressés à exécuter ces tracés :
A (r) = F(r)/m =GM/r² on rappelle µ =GM pour les astophysiciens.
courbes à tracer de r = -inf à r=+inf en oubliant pas l'intérieur de l'attracteur posé comme sphérique homogène et isotrope. et son centre r=0.
On prendra G=1, M=1, m indifférent (il n'entre pas en ligne de compte ainsi que le rayon de l'attracteur qui n'est pas dans la loi de Newton)
l'algo devra être le même sur tout le trajet de l'attracté car celui-ci ne calcule pas, il tombe indifférent au silence éternel ...
On comparera les deux courbes, et après celà on parlera de leurs écarts éventuels.
Ceci fait, il sera temps de dire si mes calculs sont faux et de combien.


Je conclu :
Archi3 vous m'imposez des opinions qui ne sont pas les miennes.

Les machines qui vont dans l'espace le sont grâce aux calculs des Ingénieurs ainsi que les machines des Physiciens qui résistent à des contraintes techniques colossales.
Les Mathématiciens on fourni les moyens aux Ingénieurs pour exécuter leurs calculs. Les Maths sont l'outil indispensable à l'artisan, mais c'est l'artisan qui met en oeuvre l'état de la science.

Concernant le dernier point :
Contrairement à l'opinion d'Einstein (130) je ne joue pas au dés...

Au plaisir de vous lire.

Ladrix (158)

[Archi3]

J'observe toujours avec une grande curiosité les stratégies de défense mises en oeuvre par certaines personnes quand on leur pose des questions très simples qui les conduiraient à dévoiler leurs contradictions si elles y répondaient : discours très longs pour détourner la question (c'est ton cas), réponses agressives personnelles , rupture brutale de la conversation, interdiction de poursuivre avec menaces de sanction (dans les cas où on a le pouvoir de le faire, ça peut aller à des conséquences plus dramatiques comme condamner quelqu'un au bûcher ou le faire interner). Ca me rappelle utilement à quel point l'humanité peut être irrationnelle sous des dehors rationnels, au cas où j'aurais tendance à l'oublier.

Bref je vous ai posé une question très simple : au cas où votre intégrale numérique ne donne pas le même résultat que l'intégrale analytique déduite de la théorie, qui est admis comme valable et sans erreur de calcul depuis des siècles, qu'est ce que vous envisagez qui puisse être remis en cause ? votre intégrale numérique, ou le résultat analytique ?

Je n'impose absolument aucune opinion, je demande juste la votre pour comprendre dans quel buts vous faites vos calculs, et ce que vous cherchez à vérifier au juste, c'est tout. Votre réponse devrait tenir en quelques lignes si vous aviez une idée claire de ce que vous cherchez à faire.

[Archi3]

Je n'ai pas eu le plaisir de voir tracée la courbe en 1/x² intégrée suivant les règles ds Mathématiciens qui nous montrerait l'exactitude du théorème de Gauss sur les coquilles vides, et du cas usuel des attracteurs pleins, et des intermédiaires plus ou moins épais.

si tu étudies un peu la physique, tu auras ce plaisir
à l'extérieur, c'est une conique : ellipse, parabole ou hyperbole suivant les conditions initiales (énergie totale spécifique 1/v^2 - GM/r négative, nulle ou positive) de foyer confondu avec le centre attracteur
à l'intérieur là où c'est plein, la force est en -kr , c'est un oscillateur harmonique, la trajectoire est une ellipse de centre confondu avec le centre attracteur
à l'intérieur quand c'est vide, F=0, la trajectoire est une droite parcourue à vitesse constante.

Les bouts de trajectoire se raccordent selon leurs conditions initiales et finales (position et vitesse finale de l'une donne la position et vitesse initiale de la suivante)

[Deedee81]

Bonjour,

J'observe toujours avec une grande curiosité les stratégies de défense mises en oeuvre par certaines personnes quand on leur pose des questions très simples qui les conduiraient à dévoiler leurs contradictions si elles y répondaient : discours très longs pour détourner la question (c'est ton cas) [...]

J'avais peu suivi cette discussion. Mais là clairement je ne peux qu'être d'accord avec toi.

Ladrix, les messages trop long, noyer les poissons, pinailler et le bavardage inconsistant et de mauvaise foi, c'est franchement pas apprécié ici.
De plus il aurait été de bon aloi de répondre aux questions car là on est en train de plonger profondément dans la violation du point 6 de la charte.

Je ne crois pas que ce dialogue de sourd s'en sorte.
Et, Archi3, je pense que tes deux derniers messages sont une bonne conclusion en soi.

Donc je vais fermer.

Merci,