Fréquence d'échantillonage : décimation

[NicoEnac]

Bonjour,

Ma question va sans doute paraître ridicule mais cela me turlupine depuis quelques jours et je ne trouve pas la réponse sur le net alors je me lance ici.

Je dispose en entrée d'échantillons audios dont la fréquence d'échantillonnage est de 48 kHz.
Mon appareil fonctionne quant à lui à 32 kHz, soit 1.5x moins vite.
Si j'avais du passer à 24 kHz, j'aurais moyenné les échantillons à 48 kHz 2 par 2 et j'aurais obtenu ce que je voulais.
Or ici, je dois faire une décimation selon un nombre non entier (1.5). Comment feriez-vous ?

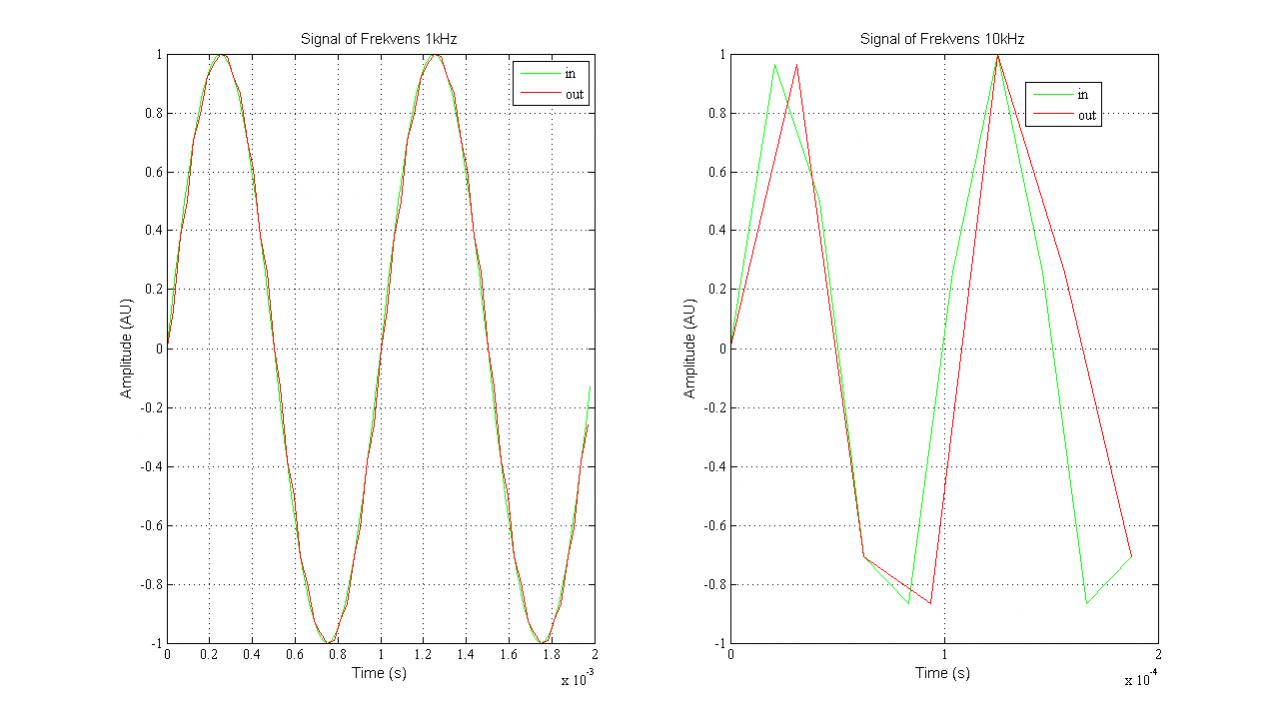
Le plus curieux, c'est que j'ai testé le principe de prendre 2 échantillons sur 3 en supprimant bêtement le 3ème et...ça marche !
Je ne m'explique pas que cela ne déforme pas horriblement le signal, du moins à l'oreille.
Cela vous semble correct ou je loupe quelque chose ?

Je vais essayer d'expliquer mieux la procédure que j'utilise :
e(n) sont mes échantillons d'entrée qui arrivent toutes les millisecondes, je les reçois donc par paquet de 48.
s(n) sont mes échantillons de sortie que j'envoie toutes les millisecondes, je les envoie donc par paquet de 32.

Pour cela, j'ai simplement fait :
s(0) = e(0)
s(1) = e(1)
s(2) = e(3) (j'ignore e(2))
s(3) = e(4)
s(4) = e(6) (j'ignore e(5))
s(5) = e(7)
etc...
s(31) = e(46) (j'ignore e(47))

Et à l'oreille, aucune dégradation !

Merci à ceux qui pourront éclairer ma lanterne !
-----

[jls28]

Salut,

moi j'ai une autre idée :

d'abord passer de 48khz à 96khz

c'est facile il suffit d'interpoler chaque paire d'échantillons successif;
(entre deux échantillons on peut en interpoller un autre).

ensuite passer de 96khz à 32khz ...

je crois que ça pourrait fonctionner...

[Gwinver]

Il y a thériquement quelques précautions à prendre.
Un signal échantillonné à 48 kHz est sussceptible d'avoir une bande passante allant jusqu'à 24 kHz, disons 20 kHz dans les faits car c'est probablement de l'audio.
Passer à 32 kHz nécessite d'abord d'effectuer un filtrage passe-bas pour éliminer tout ce qui est supérieur à 16 kHz, disons 15 kHz pour avoir un peu de marge.
Ensuite, il y a deux possibilités, passer au multiple commun de 48 kHz et 32 kHz comme suggéré par jls28, soit directement le ré-échantillonnage.
Pour toutes ces opérations, les fonctions traitement du signal d'Octave sont utilisables.
Sinon, je crois que certains logiciels libres audio ont ce genre de fonctions (filtrage passe bas et ré-échantillonnage)

[Antoane]

Bonjour,

Le plus curieux, c'est que j'ai testé le principe de prendre 2 échantillons sur 3 en supprimant bêtement le 3ème et...ça marche !
Je ne m'explique pas que cela ne déforme pas horriblement le signal, du moins à l'oreille.

Pour comparer, on va imaginer que l'oreille est un system échantillonant à 48kHz, c'est plus simple pour l'explication.
Imagines que tu envoies ce signal s généré dans un haut-parleur. L'oreille + le HP filtrent le signal. Ton oreille ensuite re-échantillone le signal s à 48kHz, qu'obtiendrais-tu ?
Un truc proche de :
e(0)=s(0)
e(1)~(2s(1)+s(0))/3=(2e(1)+e(0))/3
e(2)~(2s(1)+s(2))/3=(2s(1)+s(3))/3
e(3)~s(3)=e(3)
...
(fais un dessin si ce n'est pas clair : temps en abscisse, évolution des signaux e, s et celui mesuré à l'oreille).
Comme s varie peu entre deux échantillons, e(1)~(2e(1)+e(0))/3, e(2)~(2s(1)+s(3))/3, etc., donc le message est peu modifié.

Un exemple en image, avec en entrée un signal sinus de fréquence 1kHz à gauche et 10kHz à droite :

Dans le cas du signal 10kHz, on observe bien que la supposition "s varie peu entre deux échantillons" perd de sa validité...

Pour info le code Matlab utilisé (sur-complexe, mais permet de tester des signaux avec harmoniques), si tu veux jouer avec :

% clear
h1=1/48e3; % sampling time
f0=1e4; % frequency of the input signal
nstep=1e2; % number of samples
nstep=floor(2/(h1*f0));
t=h1*[0:nstep+1]; % time vector
harmo=[1 0 0 0 0 0 0 0 0 0 0]; % harmonic content of the signal, dc-compoennet excluded. harmo=[1 0 98 2] yields : sin(2pi*f0*t)+98*sin(2pi*3*f0*t)+2*sin(2pi*4*f0*t)
sizing=harmo'*ones(1,length(t));
In= sum(sizing.*sin(2*pi*[1:length(harmo)]'*t*f0)); % input signal

h2=1/32e3;
Out=In; % build output signal
Out(3:3:end)=[] % build output signal
t2=h2*[0:length(Out)-1]; % build time vector for output signal
figure, plot(t, In, 'g', t2, Out, 'r'), 
legend('in','out'), xlabel('Time (s)'), ylabel('Amplitude (AU)'), title(sprintf('Signal of Frekvens %i kHz',f0/1e3))
grid on

Je dispose en entrée d'échantillons audios dont la fréquence d'échantillonnage est de 48 kHz.
Mon appareil fonctionne quant à lui à 32 kHz, soit 1.5x moins vite.
Or ici, je dois faire une décimation selon un nombre non entier (1.5). Comment feriez-vous ?

Il y a plusieurs solutions, en fonction des efforts que tu veux faire et de la quantité d'information que tu veux garder.
- comme tu l'as fait : hyper-simple ;
- en interpolant les valeurs de s entre les temps d'échantillonnage :
* linéairement : s(1)=(e(1)+e(2))/2, s(2)=e(3), s(3)=(e(4)+e(5))/2...
* avec une fonction plus complexe : carré ou sinus cardinal par exemple

Si je ne m'abuse, avec une interpolation par sinus cardinal, tu ne perds aucune information du signal de départ (enfin, sauf toute la partie du spectre située au delà de 16kHz, mais ça, c'est la faute à Shannon).

[A voir en vidéo sur Futura]