Réalisation d'un circuit de conversion sinus <-> cosinus

[abdelhak64]

Merci à mes collègues,
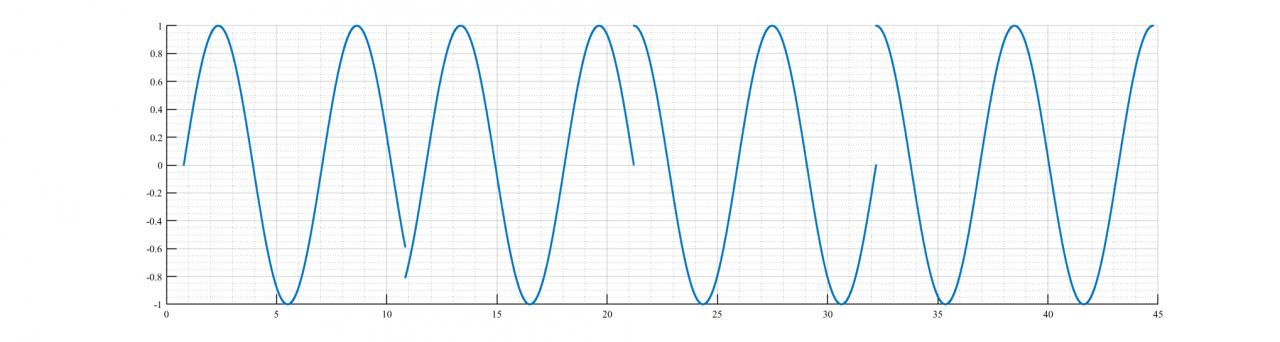
Je prépare un projet pour un rapport de stage, je me suis bloqué sur un circuit qui a pour tache de convertir le sinωt en cosωt et le cosωt en sinωt (sinωt ------>cosωt et cosωt ------> sinωt). J'ai pensé à utiliser un dérivateur ou un intégrateur mais les deux change le signe soit du cos soit du sin. et je ne peux pas utiliser un circuit inverseur car je ne dois pas l'utiliser que si le signe change. SVP si quelqu'un a une idée pour m'aider, je serai très reconnaissant et merci d'avance
-----

[penthode]

il faudrait préciser un peu le CdC....

fréquence , etc....

[abdelhak64]

Il s'agit d'un circuit qui ne va recevoir en entrée que des signaux sinusoïdaux (soit cos(ωt) ou sin(ωt) avec ω la fréquence du signal d'entrée). et en sortie je veux que le signal soit cosωt si le signal d'entrée est sin(ωt) et vice-versa et merci

[DAUDET78]

Il s'agit d'un circuit qui ne va recevoir en entrée que des signaux sinusoïdaux (soit cos(ωt) ou sin(ωt) avec ω la fréquence du signal d'entrée).

Le Monsieur te demande la valeur de la fréquence

[A voir en vidéo sur Futura]

[abdelhak64]

La valeur de la fréquence est 1KHz. Mais je veux que le circuit soit réalisable pour un intervalle autour de 1kHz

[DAUDET78]

pour un intervalle autour de 1kHz

un intervalle de combien ?
Un circuit intégrateur ou dérivateur ne fonctionne, pour un déphasage de 90°, qu'à une fréquence fixe.

Ca sert à quoi d'avoir le sinus et le cosinus dans ton utilisation ?

C'est plus facile de partir d'une fréquence carrée à 2Khz, de faire un diviseur par 2 avec deux bascules "D", et de filtrer les deux signaux de sortie qui sont en quadrature par des filtres actifs passe-bas pour obtenir des signaux analogiques cosinus et sinus .

[abdelhak64]

Dans mon projet j'essaye de réaliser une porte logique qui transforme le cosx en sinx et vesse-versa. pour la fréquence je peux prendre une fréquence constante de 1Khz.

[penthode]

une porte logique ne traite pas les signaux analogiques sinusoïdaux...

il faudrait être clair sur la demande !

[abdelhak64]

ce n'est pas une porte logique au sens classique, ça sera une porte logique qui sera utiliser dans un circuit quantique. Bien sur l'étape de la conversion sera classique mais il sera intégré dans un circuit quantique. D'ailleurs mon sujet entre dans le cadre de l'information quantique

[DAUDET78]

ce n'est pas une porte logique au sens classique, ça sera une porte logique qui sera utiliser dans un circuit quantique.

Tu peux détailler ?

[abdelhak64]

Les circuits quantiques sont des circuits qui ne sont constitués que par des composants supraconducteurs. La logique quantique utilise des qubits au lieu de bits. dans mon travail qui est évidemment théorique j'essaye de combiner des circuits quantiques avec des circuits classiques pour réaliser des taches bien définies. je te donne un exemple simple par l'algorithme de shor qui sert à factoriser un nombre entier et toutes les étapes de cet algorithme peuvent être effectuer classiquement sauf l'étape correspondante au calcul de la période qui nécessite un calculateur quantique

[DAUDET78]

Et que viens faire le sinus et le cosinus dans cette galère ?
D'où vient le 1Khz ?

[abdelhak64]

Ne te moque pas. le problème est plus délicat.

[abdelhak64]

Il veut que j'utilise le fait que sin(-x)=-sinx. or c'est une faute grave lorsqu'il s'agit d'un espace de plus de 2 dimensions

[micka_ch]

Bonjour,

Dans le cas 1 tu as uin(t)=sin(wt) et uout(t)=cos(wt)=sin(wt+90), donc ton circuit doit déphaser de +90°.
Dans le cas 2 tu as uin(t)=cos(wt) et uout(t)=sin(wt)=cos(wt-90), donc ton circuit doit déphaser de -90°.

Donc ton circuit doit réaliser 2 fonctions différentes dépendamment de l'entrée, et a moins d'avoir une référence de phase/temps absolue, on ne peut pas savoir si c'est un sinus ou un cosinus...

sin(-x)=-sinx. or c'est une faute grave lorsqu'il s'agit d'un espace de plus de 2 dimensions

là j'ai pas compris, cette identité est valide si x € R non ? ça veut dire quelque chose sin(x) si x n'est pas scalaire ? Je crois que j'ai déjà vu une définition pour le sinus d'un nombre complexe, mais jamais dans un cas pratique/physique.

Salutations

[Antoane]

Bonjour,

là j'ai pas compris, cette identité est valide si x € R non ? ça veut dire quelque chose sin(x) si x n'est pas scalaire ? Je crois que j'ai déjà vu une définition pour le sinus d'un nombre complexe, mais jamais dans un cas pratique/physique.

On peut donner du sens à sin(z) pour z complexe en passant par les formules d'Euler :
Cela aboutit d'ailleurs à une relation assez perturbante entre du sinus (que l'on a l'habitude de voir borné, dans R) et du sinus hyperbolique (que l'on a l'habitude de voir partir vers l'infini, dans R)
C'est parfois utile dans des calculs en analyse de Fourier, même si rester en exponentielles complexes est souvent, je trouve, préférable.

On peut éventuellement donner du sens au sinus d'une matrice carrée ayant les bonnes propriétés en passant par les formules d'Euler et en utilisant la définition de l'exponentielle d'une matrice, qui utilise la décomposition en série entière de l'exponentielle :

On peut aussi directement passer par la décomposition en série entière du sinus.

Pour les matrices d'autres dimensions, mis à part une application élément par élément, ou une redéfinition au cas par cas du sinus, je ne vois pas...

Pour plus de détails, voir du côté du forum de maths ou autres gens compétents



abdelhak64, il va falloir que tu décrives en détails ce que tu veux faire, pourquoi, dans quel contexte si tu veux de l'aide précise.

[abdelhak64]

Bonjour,
Voila, tu as bien compris mon problème. Je cherche un circuit qui tient compte de l'entrée. Si c'est un sinus qui est à l'entrée on doit inverser le signe (pour un dérivateur par exemple).
pour l'égalité sin(-x)=-sinx, tout le monde sait que c'est une égalité vraie. Si on ne travaille pas avec des nombres réels (sin et cos comme fonction) alors l'utilisation de cette relation peut entrainer la perte d'information sur notre signal de départ. on sait que les deux parties de l'égalité correpondent à la composition de deux fonctions f et g:

(1)- pour sin(-x): x ---f---> (-x) ---g--->sin(-x) gof(x)
(2)- pour -sin(x): x ---g--->sin(x) ---f--->-sin(x)=sin(x+π) fog(x)

Si j'utilise (2) je vais perdre l'information sur mon signal -x qui se transforme en x+π que je veux utiliser ulterierement.
Pour la question d'un espace à deux dimensions. Si on considère par exemple la rotation sur un cercle de rayon 1, alors on va voir que l'utilisation de la relation sin-x=-sinx va nous permettre de calculer le sinus mais il va automatiquement m'inverser le signe de cos. la première transformation (1) correspond à une inversion autour de l'axe horizontale tandis que la deuxième correspond à une rotation autour du centre O du cercle d'un angle de π.
Peut être que je n'ai pas bien expliqué mon problème au départ. mais j'espère que quelqu'un peut m'aider à résoudre ce problème.
En cherchant sur internet j'ai trouvé un circuit qui permet de calculer l'arcsin d'un signal
https://forum.allaboutcircuits.com/t...g-opampa.4734/
alors j'ai eu l'idée de passer de sin-x vers -x puis inverser le signe et ensuite retourner à sinus, mais là je dois trouvé un autre circuit qui me permettra de passer de x à sinx et ce sera trop long.
Merci

[Antoane]

Bonjour,

pour l'égalité sin(-x)=-sinx, tout le monde sait que c'est une égalité vraie. Si on ne travaille pas avec des nombres réels (sin et cos comme fonction) alors l'utilisation de cette relation peut entrainer la perte d'information sur notre signal de départ.

Non, ou en tous cas pas plus que dans R.

on sait que les deux parties de l'égalité correpondent à la composition de deux fonctions f et g:

(1)- pour sin(-x): x ---f---> (-x) ---g--->sin(-x) gof(x)
(2)- pour -sin(x): x ---g--->sin(x) ---f--->-sin(x)=sin(x+π) fog(x)

Si j'utilise (2) je vais perdre l'information sur mon signal -x qui se transforme en x+π que je veux utiliser ulterierement.

Si tu utilises (2), tu obtiens en sortie -sin(x) = sin(-x) = sin(x+π) = sin(x+3864261π). Il y a la même perte d'information dans les trois cas : celle due à la surjectivité du sinus sur l'espace considéré.
x existe encore, il peut encore servir si besoin : tu peux envoyer (le même) x sur trois (ou plus) blocs différents :
- un qui applique la fonction sin ;
- un qui applique la fonction cos ;
- un qui applique la fonction identité ;
- etc.
Et faire ce que tu veux des sorties.

Si tu as du mal à manipuler le concept de sinus d'argument complexe, utilise les exponentielles complexes. Ou même leur développement en série entière.

Pour la question d'un espace à deux dimensions. Si on considère par exemple la rotation sur un cercle de rayon 1, alors on va voir que l'utilisation de la relation sin-x=-sinx va nous permettre de calculer le sinus mais il va automatiquement m'inverser le signe de cos.

Non. Essaye de démontrer proprement, formellement que :

Ou bien écrit proprement, formellement, ce qui te pose problème.

La première transformation (1) correspond à une inversion autour de l'axe horizontale tandis que la deuxième correspond à une rotation autour du centre O du cercle d'un angle de π.

Pas une inversion, une symétrie.
Tout ça est très nébuleux essaye de mettre au clair tes idées, de formaliser proprement ton raisonnement. Pour l'instant, tu écris des faits établis et bien connus pour arriver au dernier moment, par un coup de baguette magique, à une conclusion assez extraordinaire.


Ce qu'on regarde quant on prend la projection d'un point (du cercle trigo) sur l'axe des ordonnées n'est pas le sinus du point mais le sinus de son argument - qui est un réel.

Mais on s'éloigne du problème...

Peut être que je n'ai pas bien expliqué mon problème au départ.

Je pense qu'on est à peu près tous d'accord
Essaye de nous faire un schéma indiquant clairement :
- d'où vient le (ou les) signal d'entrée (par que système est-il généré), par rapport à quoi il est synchronisé (en l'absence de synchronisation externe, sinus et cosinus sont identiques) ;
- vers quoi sont dirigés les signaux de sortie, à quoi ils servent.

[abdelhak64]

L'exposition du problème et plus simple et la discussion nous a fait dérouter de mon problème essentiel. qui est le suivant:
Réalisation d'un circuit qui permet la transformation suivante:
(Uin:sinωt ------>Uout:cosωt et Uin:cosωt ------> Uout:sinωt)
si j'utilise un dérivateur j'aurai
(sinωt ------>-cosωt et cosωt ------> sinωt)
si j'utilise un inverseur plus un dérivateur j'aurai
(sinωt ------>cosωt et cosωt ------> -sinωt)
pour les paramètres de mon signal tel que la fréquence je peux les adapter au circuit.
En ce qui concerne la discussion sur le sinus ce que tu as commenter est valable tant qu'on n'as pas ajouter une phase au circuit. à savoir que le passage de sin<---> cos correspond à ajouter ou soustraire une phase de 90°

[Antoane]

Réalisation d'un circuit qui permet la transformation suivante:
(Uin:sinωt ------>Uout:cosωt et Uin:cosωt ------> Uout:sinωt)

Ton circuit n'a qu'une unique entrée et doit seul deviner s'il s'agit d'un sinus ou d'un cos ?
- si oui : c'est a priori impossible, il faut une référence des phase, i.e. un temps défini comme le temps zéro. Quelle est donc ta référence ? ;
- si non : j'ai toujours pas compris

En ce qui concerne la discussion sur le sinus ce que tu as commenter est valable tant qu'on n'as pas ajouter une phase au circuit. à savoir que le passage de sin<---> cos correspond à ajouter ou soustraire une phase de 90°

[abdelhak64]

Merci Antoine pour ta réponse. C'est justement ce que tu viens de dire. mon circuit n'as qu'une seule entrée et il dois deviner si c'est un cosinus ou un sinus (càd il doit agir suivant la phase du signale qui est soit 0 ou 90°). pour la référence de phase excuse moi je n'ai aucune idée sur la notion de "référence de phase".

[DAUDET78]

pour la référence de phase excuse moi je n'ai aucune idée sur la notion de "référence de phase".

Si tu as un signal alternatif, comment peux tu savoir si c'est un sinus ou un cosinus ? c'est la même forme !
La différence entre un sinus et un cosinus, c'est sa valeur au temps t=0 ("référence de phase")
- si la valeur du signal est 0, c'est un sinus.
- si la valeur du signal est au max, c'est un cosinus.

[abdelhak64]

Merci DAUDET78, mais comment je peux l'utiliser dans mon circuit

[Antoane]

Est-ce que ton signal ressemble à ça :


Pendant quelques périodes c'est un sinus, pendant quelques autre c'est un cos, et ainsi de suite?

[abdelhak64]

Mon signal est exactement pareil mais l'alternance entre le cos et le sin n'est pas ordonné.

[PA5CAL]

Bonsoir

Comme indiqué plus haut, en plus du signal d'entrée, il est nécessaire de disposer d'une référence temporelle, concrète ou virtuelle, permettant de dire si la portion de sinusoïde produire à un instant donné est un sinus ou un cosinus.

Cette référence pourrait être par exemple un signal d'horloge synchronisé avec la sinusoïde, ou bien une impulsion produite à t=0.

A défaut, si les portions de sinusoïde sont exclusivement et strictement de la forme U₀.sin(ωt) et U₀.cos(ωt), alors il n'est possible de savoir à quelles formes on a affaire qu'après le premier changement d'une forme à l'autre. Dans l'exemple de signal d'Antoane (#24), le premier changement permet de déduite qu'on est passé de sinus à cosinus cas le signe de l'ancienne forme correspond au signe de la dérivée de la nouvelle forme.

Partant, chaque discontinuité dans le signal d'entrée ou dans sa dérivée indique un changement de forme, et donc peut servir à produire la forme souhaitée du signal de sortie (cela pourrait se limiter à changer de façon convenable le signe d'un signal correspondant de la dérivée du signal d'entrée).

De quoi disposes-tu actuellement en terme de référence temporelle ?

[abdelhak64]

Bonjour, je veux remercier tous les gens qui ont participé à cette discussion et qui m'ont aidé à situé au moins les fils à suivre pour résoudre mon problème. tout simplement pour récapituler j'ai deux voies à suivre:
1- Utiliser une référence de phase comme m'a proposé Antoane. J'ai commencé déjà à me documenter à ce sujet malgré des difficultés trouvés pour avoir des documents en Francais et qui traitent un peu de la théorie.
2- Il y'a un autre voie que je ne sais pas si il donnera quelque chose et que j'explique comme suit:
Le seul changement de phase qui me permet de faire une conversion entre le cos et le sin c'est de changer la phase (wt) en (-wt+90°). à savoir que
sin(-wt+90°)=coswt et cos(-wt+90°)=sinwt.
Voila donc les étapes que je dois suivre: sin(wt)---1--->(wt)---2--->(-wt)---3--->(-wt+90°)---4--->sin(-wt+90°)=cos(wt)
ce qui est intéressant dans cette méthode c'est que cette transformation me donnent le résultat indépendamment du signal d'entrée. voila pour le cos:
cos(wt)=sin(-wt+90°)---1--->(-wt+90°)---2--->(wt-90°)---3--->(wt)---4--->sin(wt)
l'étape 1 correspond à un circuit de calcul de arcsin que j'ai déjà donné le lien
l'étape 2 correspond à une inversion de signe. pas de problème
l'étape 3 correspond à l'ajout d'une phase . pas de problème également
mais c'est l'étape 4 qui me posera un problème.
Merci beaucoup mes collègues. je vais vous informer de tout avancement à ce sujet et de votre part si quelqu'un peut encore me donner quelque chose d'utile je serai très reconnaissant

[Antoane]

Bonjour,

Il n'est pas possible de faire ce que souhaites en ne faisant qu'appliquer une fonction (aussi complexe soit-elle, impliquant arcsin, sin, cos, etc.) au signal. Tu peux t'en convaincre en supposant que tu est capable de reproduire électroniquement toutes les fonctions mathématiques que tu connais.
Ta méthode consistant à utiliser arcsin ne fonctionne que sur [-pi, pi].
Une solution est de passer par une détection des transitions entre les états (comme proposé par PA5CAL), ou bien d'obtenir une référence de temps (ou de phase, c'est pareil).

Pour la mise en oeuvre, je ne connais pas grand chose à ce domaine mais n'y a-t-il rien à récupérer du côté des démodulateurs / modulateurs I-Q ?
Sinon : DSP ou micro-contrôleur

[abdelhak64]

Bonjour,
Merci Antoane pour votre soutien. Je vais essayer de voir toutes les solutions que tu m'as proposé. D'ailleurs pour l'autre méthode je n'ai trouvé que des circuits qui convertissent des signaux périodiques comme le signal carré en signal sinus mais pas pour un signal sous forme d'une droite linéaire (x=wt)