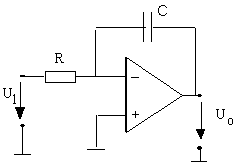
AOP : 1/jw = intégration ?
Discussions similaires
-
Par invite69ee30f1 dans le forum Mathématiques du supérieur
Réponses: 2
Dernier message: 09/03/2015, 20h59
-
Par invite00c17237 dans le forum Mathématiques du supérieur
Réponses: 1
Dernier message: 26/01/2014, 23h22
-
Par invite6997af78 dans le forum Mathématiques du supérieur
Réponses: 9
Dernier message: 13/11/2011, 20h45
-
Par invite204ce29c dans le forum Physique
Réponses: 6
Dernier message: 27/02/2007, 15h36
-
Par invite781ac61b dans le forum Physique
Réponses: 4
Dernier message: 06/01/2007, 19h01