Bonjour,
Je voulais faire part d'un problème de maths lié à l'électronique, que j'ai mis trois semaines à résoudre.
Pourtant, après avoir trouvé la solution, je me dis : C'était pourtant pas si difficile !
Ce problème sert à calculer les résistances à mettre autour d'un comparateur à hystérésis pour avoir les seuils VT+ et VT- voulus, tenant compte des tensions d'alim, VsatMAX, VsatMIN liés au comparateur utilisé.
Et cela pour deux types :
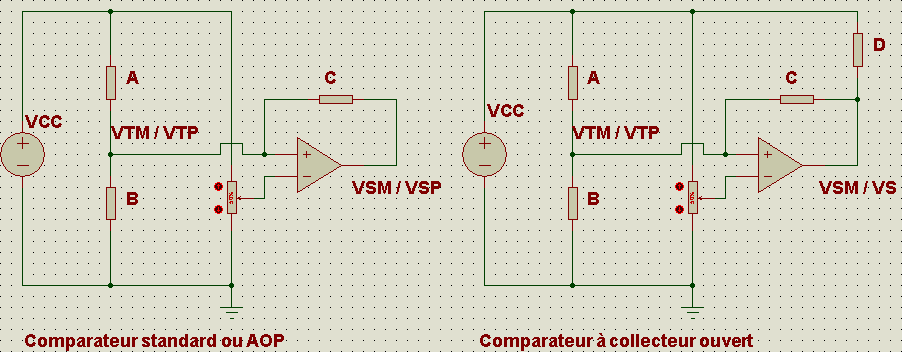
- Le comparateur "standard" donnant des tensions min et max égales à VsatMIN, VsatMAX
- Le comparateur à collecteur ouvert comme le célèbre LM311. Dans ce cas, on a VsatMIN, mais VsatMAX est inexistant ici.
Quand V+ > V-, la sortie est flottante, c et d sont donc en série. Le calcul de c n'est alors pas difficile pour avoir le vs voulu entre c et d(voir schéma)
Le choix de cette tension est prévue dans les calculs.
Le calcul consiste à écrire les formules de courants dans les deux états possibles du comparateur, et de passer par un système d'équations pour déduire les valeur de résistances.
Pour le cas du collecteur ouvert, et vu le schéma, il parait évident qu'il faille choisir un vs compris entre VT+ et VCC.
Il existe aussi des cas impossibles, avec des résistances calculées infinies ou négatives, je ne me suis pas penché là dessus.
Code:vcc : Tension d'alim vtm : Seuil VT- vtp : Seuil VT+ vsm : Vsat- (VsatMIN) vsp : Vsat+ (VsatMAX) vs : Tension de sortie voulue entre RC et RD lorsque la sortie est flottante. a : RA b : RB c : RC d : RD
Comparateur standard
Calculs pour atteindre VT- (V+ < V-, Comparateur à l'état bas)
On fixe c pour éviter une infinité de solutions. De l'ordre de 100k pour le pas trop charger la sortie en courant et faire bouger VsatMIN, VsatMAX
Formules réécrites sous la forme i=u/r.Code:ia = ib + ic // Loi des noeuds
Tension sur a (Ua) écrite : (vcc - vtm) car "Ua" n'est pas fixe et dépend de l'état du comparateur. Même logique pour "Uc" écrite sous la forme (vtm - vsm)
A partir de ce résultat, on peux déduire b lorsque le comparateur a changé d'état :Code:vcc - vtm vtm vtm - vsm --------------- = --------------- + --------------- a b c vcc - vtm c*vtm b*vtm - b*vsm --------------- = --------------- + --------------- a b*c b*c vcc - vtm c*vtm b*vtm - b*vsm --------------- = --------------- + --------------- a b*c b*c vcc - vtm c*vtm + b*vtm - b*vsm --------------- = -------------------------------- a b*c b*c*(vcc - vtm) = a(c*vtm + b*vtm - b*vsm) b*c*vcc - b*c*vtm = a*c*vtm + a*b*vtm - a*b*vsm b*c*vcc - b*c*vtm - a*b*vtm + a*b*vsm = a*c*vtm b(c*vcc - c*vtm - a*vtm + a*vsm) = a*c*vtm a*c*vtm b = ----------------------------- c*vcc - c*vtm - a*vtm + a*vsm
vtm devient vtp
vsm devient vsp
A partir de ces deux formules de b, on peut écrire le système d'équations :Code:a*c*vtp b = ----------------------------- c*vcc - c*vtp - a*vtp + a*vsp
Code:b(c*vcc - c*vtm - a*vtm + a*vsm) = a*c*vtm b(c*vcc - c*vtp - a*vtp + a*vsp) = a*c*vtp b*c*vcc - b*c*vtm - a*b*vtm + a*b*vsm = a*c*vtm b*c*vcc - b*c*vtp - a*b*vtp + a*b*vsp = a*c*vtp b*c*vcc*vtp - b*c*vtm*vtp - a*b*vtm*vtp + a*b*vsm*vtp = a*c*vtm*vtp // Multiplie par vtp b*c*vcc*vtm - b*c*vtm*vtp - a*b*vtm*vtp + a*b*vsp*vtm = a*c*vtm*vtp // Multiplie par vtm b*c*vcc*vtp - b*c*vtm*vtp - a*b*vtm*vtp + a*b*vsm*vtp = a*c*vtm*vtp b*c*vcc*vtm - b*c*vtm*vtp - a*b*vtm*vtp + a*b*vsp*vtm = a*c*vtm*vtp -- ------------------------------------------------------------------------ b*c*vcc*vtp-b*c*vcc*vtm + 0 + 0 + a*b*vsm*vtp - a*b*vsp*vtm = 0 b*c*vcc*vtp - b*c*vcc*vtm + a*b*vsm*vtp - a*b*vsp*vtm = 0 b*c*vcc*vtp + a*b*vsm*vtp = a*b*vsp*vtm + b*c*vcc*vtm b(c*vcc*vtp + a*vsm*vtp) = b(a*vsp*vtm + c*vcc*vtm) // Factorise par b, qui sera éliminé à la ligne suivante c*vcc*vtp + a*vsm*vtp = a*vsp*vtm + c*vcc*vtm // Plus de b dans le calcul a*vsm*vtp - a*vsp*vtm = c*vcc*vtm - c*vcc*vtp -a*vsm*vtp + a*vsp*vtm = - c*vcc*vtm + c*vcc*vtp // * (-1) a*vsp*vtm - a*vsm*vtp = c*vcc*vtp - c*vcc*vtm a(vsp*vtm - vsm*vtp) = c*vcc*vtp - c*vcc*vtm c*vcc*vtp - c*vcc*vtm a = --------------------- // Ne dépend plus de b vsp*vtm - vsm*vtp c*vcc*vtp - c*vcc*vtm a = --------------------- vsp*vtm - vsm*vtp a*c*vtp b = ----------------------------- c*vcc - c*vtp - a*vtp + a*vsp
Comparateur de type collecteur ouvert
Comparateur en haute impédance
On est dans le cas où V+ > V-
Calculs pour atteindre VT+
On fixe d pour éviter une d'avoir une infinité de solutions.Code:vtp = ub // La tension "Ub" est la tension de seuil VT+
c et d en série (ic = id), sortie flottante.
Dimensionner c pour fixer la tension de sortie d'état haut, notée vs
On ne laisse pas "Uc", "Ud" écrites telles-quelles, car ces tensions ne sont pas fixes et dépendent de l'état du comparateur.Code:uc c = --------------- ic vs - vtp c = --------------- // de la forme r=u/i ud ----- d
Code:vs - vtp c = --------------- vcc - vs ---------- d d c = (vs - vtp) * ---------- vcc - vs d*vs - d*vtp c = -------------- vcc - vs
Pour calculer a, on a besoin de passer par les courants, et la loi des noeuds
Donc :Code:ib = ia + ic
En faisant un système d'équations, trouver une expression de a indépendante de bCode:ia = ib - ic
Réécrite avec les courants sous la forme i=u/r
Extraire bCode:vcc - vtp vtp vs - vtp --------------- = --------------- - --------------- a b c vcc - vtp c*vtp b*vs - b*vtp --------------- = --------------- - --------------- a b*c b*c vcc - vtp c*vtp - (b*vs - b*vtp) --------------- = ------------------------ a b*c vcc - vtp c*vtp - b*vs + b*vtp --------------- = ------------------------ a b*c b*c*(vcc - vtp) = a(c*vtp - b*vs + b*vtp) a(c*vtp - b*vs + b*vtp) = b*c*vcc - b*c*vtp // Repère 1 b*c*vcc - b*c*vtp a = -------------------- c*vtp - b*vs + b*vtp
Calculs pour atteindre VT-Code:a(c*vtp - b*vs + b*vtp) = b*c*vcc - b*c*vtp a*c*vtp - a*b*vs + a*b*vtp = b*c*vcc - b*c*vtp a*c*vtp = a*b*vs - a*b*vtp + b*c*vcc - b*c*vtp b(a*vs - a*vtp + c*vcc - c*vtp) = a*c*vtp a*c*vtp b = ---------------------------- a*vs - a*vtp + c*vcc - c*vtp
Code:vtm = ub // La tension "Ub" est la tension de seuil VT- ib = ia + ic vtm vcc - vtm vsm - vtm ------------ = ------------ + ------------ b a c vtm c*vcc - c*vtm a*vsm - a*vtm ------------ = ------------- + ------------- b a*c a*c a*c*vtm = b(c*vcc - c*vtm + a*vsm - a*vtm) a*c*vtm - a*b*vsm + a*b*vtm = b*c*vcc - b*c*vtm // Repère 2 Système d'équation avec les deux formules des courants selon l'état du comparateur : a(c*vtp - b*vs + b*vtp) = b*c*vcc - b*c*vtp // Récupère le Repère 1 a*c*vtm - a*b*vsm + a*b*vtm = b*c*vcc - b*c*vtm // Récupère le Repère 2 a*c*vtp - a*b*vs + a*b*vtp = b*c*vcc - b*c*vtp a*c*vtm - a*b*vsm + a*b*vtm = b*c*vcc - b*c*vtm a*c*vtm*vtp - a*b*vs*vtm + a*b*vtm*vtp = b*c*vcc*vtm - b*c*vtm*vtp // Multiplie par vtm a*c*vtm*vtp - a*b*vsm*vtp + a*b*vtm*vtp = b*c*vcc*vtp - b*c*vtm*vtp // Multiplie par vtp a*c*vtm*vtp - a*b*vs*vtm + a*b*vtm*vtp = b*c*vcc*vtm - b*c*vtm*vtp a*c*vtm*vtp - a*b*vsm*vtp + a*b*vtm*vtp = b*c*vcc*vtp - b*c*vtm*vtp -- ----------------------------------------------------------------------- - a*b*vs*vtm + a*b*vsm*vtp = b*c*vcc*vtm - b*c*vcc*vtp - a*b*vs*vtm + a*b*vsm*vtp = b*c*vcc*vtm - b*c*vcc*vtp a*b*vs*vtm - a*b*vsm*vtp = b*c*vcc*vtp - b*c*vcc*vtm b(a*vs*vtm - a*vsm*vtp) = b(c*vcc*vtp - c*vcc*vtm) // Factorise par b, qui sera éliminé à la ligne suivante a*vs*vtm - a*vsm*vtp = c*vcc*vtp - c*vcc*vtm // Plus de b dans le calcul a(vs*vtm - vsm*vtp) = c*vcc*vtp - c*vcc*vtm c*vcc*vtp - c*vcc*vtm a = --------------------- vs*vtm - vsm*vtp d*vs - d*vtp c = -------------- vcc - vs c*vcc*vtp - c*vcc*vtm a = --------------------- vs*vtm - vsm*vtp a*c*vtp b = ---------------------------- a*vs - a*vtp + c*vcc - c*vtp
-----