CAN/CNA diviser par 2^n ou 2^n-1

[totola]

Bonjour,

J’ai toujours eu du mal à comprendre pourquoi pour un CNA on définit le pas en divisant la pleine échelle par 2^n – 1 alors qu’on divise par 2^n pour le CAN.

Je trouve aucune ressource expliquant cette différence. J’ai donc creusé un peu le sujet et je suis arrivé à l*‘explication suivante. J’aimerais bien avoir un retour afin de savoir si je ne fais pas complètement fausse route. Merci

Je prends l’exemple d’une conversion sur 3 bits.

Pour le CAN*:

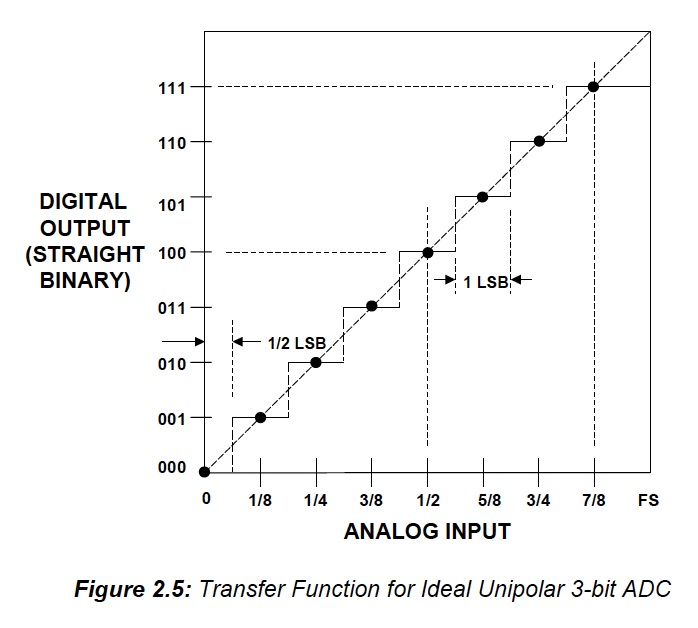
[0;1q[ → 000
[1q;2q[ → 001
[2q;3q[ → 010
[3q;4q[ → 011
[4q;5q[ → 100
[5q;6q[ → 101
[6q;7q[ →110
[7q;8q[ → 111

On découpe bien la plage de tension en 8 intervalles et on affecte une valeur numérique par plage de tension. La division par 2^n est évidente.

Pour le CNA*:

1) si je choisis d’effectuer la conversion inverse en choisissant de diviser par 2^n aussi (et pourquoi pas??)*:

000 → 0q
001 → 1q
010 → 2q
011 → 3q
100 → 4q
101 → 5q
110 → 6q
111 → 7q

Ce qui fait que je sous estime systématiquement la valeur analogique d’origine de 1q au maximum*:

par exemple*:

- une tension de 0.9q est numérisée en 000 et sera restituée à 0q → on sous estime de 1q max
- une tension de 7.9q est numérisée en 111 et sera restituée à 7q → on sous estime de 1q max
- une tension de 3.9q est numérisée en 011 et sera restituée à 3q → on sous estime de 1q max
etc.

2) si je choisis un pas en divisant cette fois pas 2^n-1 (et pourquoi pas non plus?)*:

Alors par rapport au CAN j’obtiens un nouveau pas q’ = 1.14q (environ)


000 → 0q’ = 0q
001 → 1q’ = 1.14q
010 → 2q’= 2.29q
011 → 3q’= 3.43q
100 → 4q’= 4.57q
101 → 5q’= 5.71q
110 → 6q’= 6.86q
111 → 7q’ = 8q

à ce moment là*:

- une tension de 0.9q est toujours numérisée par le CAN à 000 et sera toujours restituée à 0q donc toujours une sous estimation de 1q max dans ce cas.
- une tension de de 7.9q est numérisée par le CAN en 111 et sera restituée à 7q’=8q, cette fois ci on surestime de 1q max (ce qui n’est pas vraiment plus grave..)
- En revanche, une tension de 3.9q numérisée en 011 sera restituée à 3q’=3.43q soit environ au milieu de l’intervalle et grosso modo on va avoir une erreur max de + ou – 0.5q ce qui est mieux que dans le cas précédent où on sous-estime systématiquement de 1q max.

En résumé, je dirais que diviser par 2^n – 1 dans le cas de la restitution permet de conserver une erreur max de 1q aux extrémités de la caractéristiques mais de réduire cette erreur à 0.5q (en plus ou en moins) au voisinage du milieu de la caractéristique. Ce qui est théoriquement mieux en effet.

Maintenant je rajouterais quand même qu’à partir d’un certain nombre de bits, en pratique cette différence doit devenir très largement négligeable par rapport aux autres erreurs… Donc pourquoi se casser la tête et ne pas diviser par 2^n dans tous les cas…*?? J’avoue que je n’ai pas de réponse là dessus…


Merci de vos retours
-----

[Vincent PETIT]

Bonjour,
Le problème que tu vois est le même que pour une boucle en langage informatique C. En langage C si tu veux faire une boucle de 10 itérations tu peux faire une boucle qui démarre de 0 jusque 9

for (int i = 0; i <= 9; i++)
{
   ... /* 10 itérations allant de 0 à 9 inclus */
}

ou alors

for (int i = 0; i < 10; i++)
{
   ... /* 10 itérations allant de 0 à 10 exclus, donc de 0 à 9 au final */
}

Pour les ADC et les DAC, le résultat de la conversion démarre forcément de 0 et pas de la valeur 1. Le fait qu'on démarre de 0 amène à faire un -1 à la fin comme dans les boucles en langage C par exemple.

Les puristes utilisent V_REF/2^N-1 parce que mathématiquement c'est ce qui se passe mais faire V_REF/2^N en ayant connaissance des défauts de l'ADC, ou du DAC, (INL, DNL, le bruit) donne un résultat tellement proche que ça revient au même.


ps : dans ton exemple de CNA ou CAN de 3 bits, le résultat est contenu dans 8 valeurs mais allant de 0 à 7. D'où le -1 dans la formule du puriste.

[Jack]

Les puristes utilisent V_REF/2^N-1 parce que mathématiquement c'est ce qui se passe mais faire V_REF/2^N en ayant connaissance des défauts de l'ADC

Je ne suis pas d'accord.
Pour moi, il faut bien diviser par 2ⁿ.

Prenons le cas du plus simple des ADC: le comparateur. Avec un Vref de 8V pour simplifier, nous aurons bien '0' pour une tension 0V < Vin < 4V et '1' pour 4V < Vin < 8V. Le quantum est bien égal à Vref/2^N = 8/2 = 4V, le nombre de bits N étant égal à 1.
Pour un ADC 2 bits:
00 -> 0V à 2V
01 -> 2V à 4V
10 -> 4V à 6V
11 -> 6V à 8V
q = 8/4 = 2V

[totola]

Oui, c'est tout à fait ça pour l'ADC. Ma remarque portait sur le DAC à savoir la conversion inverse. Toute la littérature sur le sujet indique une division par 2^n-1. Je proposais une explication que je n'ai lue nulle part, voilà pourquoi je cherche des avis à ce sujet.

Merci.

[A voir en vidéo sur Futura]

[Jack]

De nombreux DAC divisent par 2^N. C'est d'ailleurs le principe de base come énoncé dans ce document d'ANALOG DEVICE qui est un des principaux (ou le principal?) fabricants de ce type de composants.

Ce qui gène, c'est qu'on arrive pas à générer V_FS (Full Scale) en sortie. En effet, pour un convertisseur 8 bits, Vout_max = V_FS x 255 /256 alors qu'en divisant par 2^N-1 = 255, Vout_max = V_FS x 255 /255 = V_FS.
Mais il suffit de regarder la doc de DAC ou d'ADC pour constater que pour la plupart, on a bien affaire à une division par 2^N.

[Jack]

Toute la littérature sur le sujet indique une division par 2^n-1

Quelle littérature?
En général, les cours délivrés par les profs de physique appliquée divisent en effet par 2^N-1

[Vincent PETIT]

Il me semble aussi que dans toutes les docs j'ai pu lire, y compris le document d'Analog Devices que tu cites, il est question de (2N)-1.

Il est écrit en bas de la page 2.4 (page 5 du navigateur) qui donne l'exemple d'un ADC 3 bits

The full-scale analog input voltage is defined by 7/8 FS, (FS – 1 LSB).

Après entendons nous bien, ça ne fait quasiment aucune différence.

Pour reprendre l'exemple de Jack

Pour un ADC 2 bits:
00 -> 0V à 1 999V
01 -> 2V à 3,999V
10 -> 4V à 5,999V
11 -> 6V à 7,999V

[Jack]

On parle du quantum, donc de l'intervalle analogique correspondant à une modification d'un bit de la valeur numérique.
Pour calculer la valeur du quantum q, on divise par 2^N et pas 2^N-1.

C'est ce qui explique le "7/8 FS, (FS – 1 LSB)" auquel tu fais allusion et qui est le "problème" que je citais dans un message précédent au sujet des DAC: on n'arrive pas à la valeur pleine échelle.
Quant à l'ADC, la plage de tension correspondant à la valeur numérique est comprise entre (V_FS – q) et VFS. Ca me semble logique et cohérent vu qu'une valeur numérique nulle correspond à la plage 0 à q.

Je crois qu'en fait on veut dire la même chose mais si on veut être précis, pour le calcul du quantum, il faut bien diviser par 2^N .

[gts2]

Bonjour,

Le point de vue DAC ADC n'est pas tout à fait symétrique
- ADC, on associe à des intervalles les valeurs 0,1,2,3 cela fait fait bien quatre intervalles qui couvre 0-4q soit 2ⁿ
- DAC, on associe aux valeurs 0,1,2,3 les tension 0 1q 2q 3q, la valeur max vaut bien 3q soit 2^n-1 si on définit q par rapport à Vmax ; dit autrement le DAC renvoie le début de l'intervalle de l'ADC

Pour ce qui est de l'erreur de 1q, les ADC décalent (toujours ?) de 1/2LSB et donc 0 correspond à 0-q/2, ce qui crée une erreur de +-q/2 et non 0-q ; cela pose juste un problème à pleine échelle.

[polo974]

Dans le pdf:

Notice that there are 16 distinct possible levels, ranging from the all-zeros code 0000, to the all-ones code 1111.
It is important to note that the analog value represented by the all-ones code is not full-scale (abbreviated FS), but FS – 1 LSB.
This is a common convention in data conversion notation and applies to both ADCs and DACs.

soit en français:

Notez qu'il existe 16 niveaux possibles distincts, allant du code composé uniquement de zéros 0000 au code composé uniquement de uns 1111.
Il est important de noter que la valeur analogique représentée par le code tout à un n'est pas pleine échelle (en abrégé FS), mais FS – 1 LSB.
Il s'agit d'une convention courante dans la notation de conversion de données et s'applique à la fois aux ADC et aux DAC.

C'est une convention, où en fait on prend en gros Vref comme valeur Full Scale, et non la valeur max sortie du CNA (DAC).

C'est assez pratique, car Vref est une entrée du système, et non une sortie. Et comme les ingés sont en général des gens pratiques...

[Jack]

Pour ce qui est de l'erreur de 1q, les ADC décalent (toujours ?) de 1/2LSB et donc 0 correspond à 0-q/2, ce qui crée une erreur de +-q/2 et non 0-q ; cela pose juste un problème à pleine échelle.

Non, ce n'est pas systématique.
Je pense qu'il faut tout simplement consulter la doc du composant que l'on compte utiliser.

[totola]

Ok, merci de la réponse et pour le partage du pdf.
En effet, le mieux est de consulter la doc.

[jiherve]

bonjour,

il y a des amateurs de diptères ici, car si la question peut se poser pour 4 ou 6 bits mais à partir de 8bits on taquine sous le % donc souvent mieux que les conditionnements amont/aval.
Néanmoins pour vous occuper je vous soumets le problème suivant: que peut on faire des bits (lsb) inutilisés sur un DAC 10bits utilisé en 8 ou 6 bits ?
JR

[antek]

Dans ce cas ce sont les "hsb" qui sont inutilisés, non ?
Ka ne m'a pas trop occupé, je me suis contenté d'attendre la réponse, et de toute façon je ne vois pas

[jiherve]

bonjour,
en général on utilisera les msb pour garder la dynamique mais dans certains cas (imagerie couleur) il faudra bricoler les lsb.
JR

[totola]

Bonjour,
si je comprends bien ce doc

DAC.png

dac2.png

Vfull scale = 4.095 V et pour ce DAC 12bits il faut bien effectuer 4.095 / (2^12 -1) pour retrouver 1mV/bit annoncé

[jiherve]

bonjour,
oui 2^12 -1 = 0xFFF= 4095.
mais si tu divises par 4096, ce qui est plus facile car c'est un bête décalage ,tu commets une erreur de 25ppm et en général c'est dans le bruit!
JR

[Jack]

Ob divise bien par 4096 et pas 4095: de 0 à 4095 ça fait bien 4096 valeurs