Bonjour,
Dans le post sur l'axiome des parties est évoqué l'univers constructible de Von Neuman.
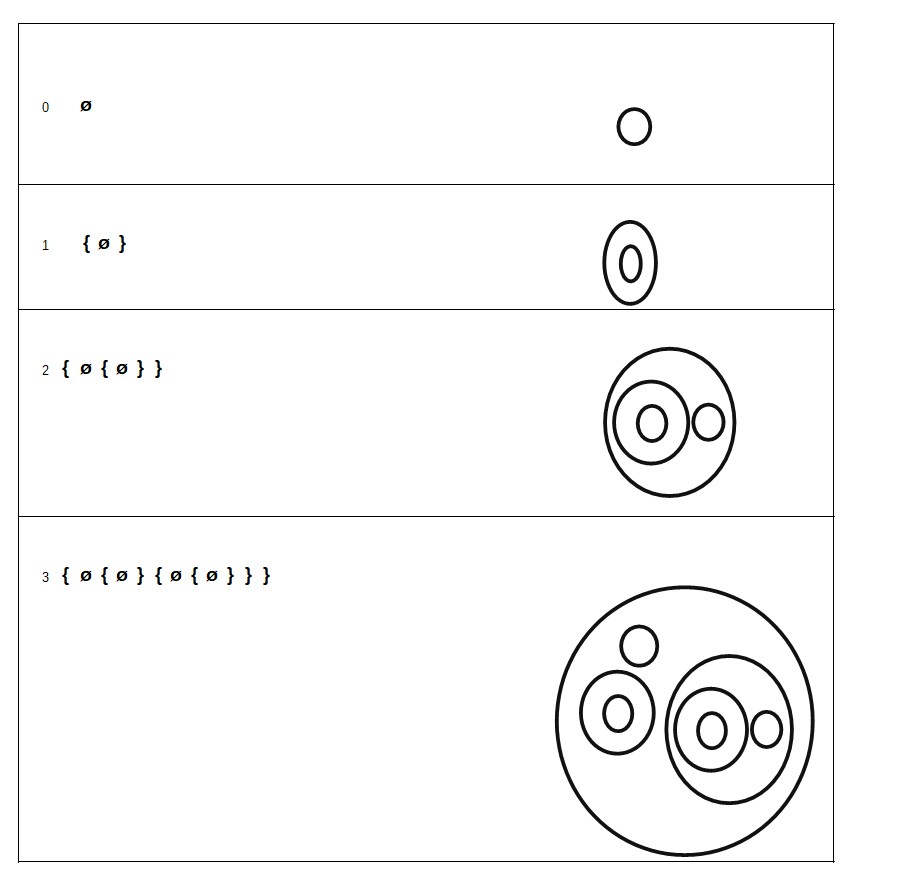
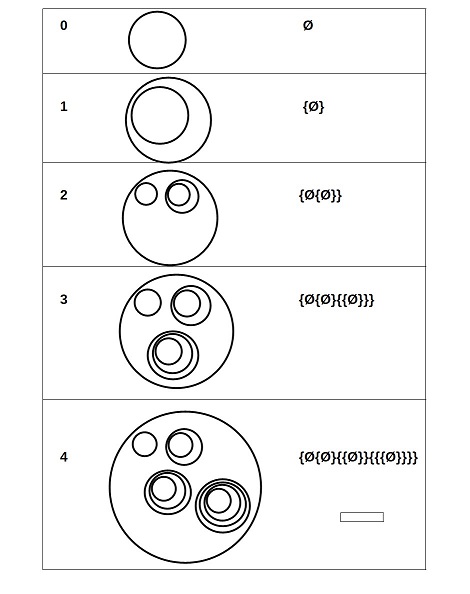
Je pense avoir saisi l'idée pour la construction mais je souhaite une confirmation, En indexant selon les ordinaux je représente cette construction ainsi (avec les nombres= indexations, l'écriture en extension et les diagrammes de VENN correspondants aux index):
Est ce correct?
Sans questions il n'y a que des problèmes sans réponses.
Bonjour,
On parle d'univers constructible seulement pour la construction selon Gödel. Ici on dit simplement univers de Von Neuman. Et il manque un élément à ta dernière étape.
Non il ne manque rien a la derniere etape, mais par contre je ne vois pas ce qu'apporte ces diagrammes a la comprehension du phenomene..Envoyé par Superbenji
Ce dont il s'agit ici, c'est la construction des ordinaux de Von Neumann.
Ah oui en effet. J'avais compris que les diagramme correspondaient à l'ensemble des parties de l'ensemble précédent... Du coup oui, c'est peut être des ordinaux dont il parlais.
Ouf
En fait j'avais pas compris ce qu'était un sous ensemble, j'avais cette idée en tête:
{} : 1 ensemble que je note A
{{}} : 1 ensemble B qui a le sous ensemble A pour élément
{{{}}} : 1 ensemble C ayant pour sous ensembles A et B au lieu de simplement voir un ensemble C qui a pour sous ensemble l'ensemble B.
Sans questions il n'y a que des problèmes sans réponses.
Petit édit coloré qui correspond à avertir le lecteur sur la qualité douteuse de ce que je peux écrire... la partie 1 de la phrase ci dessus me semble fausse mais la partie 2 pas forcement claire, car dans l'idée de la compréhension en dessinant autrement j’obtiens le diagramme ci dessous dans lequel j'identifie que la couleur entourant un cercle rempli de couleur (l'ensemble vide) peut-être considérée comme délimitant un ensemble (lui même sous ensemble) hors pour {{{}}} cela ne fonctionne pas car cercle noir entouré par un anneau blanc puis un anneau noir etc.. il reste quelque chose que je n'ai pas encore compris à mon avis.
Dernière modification par Liet Kynes ; 03/10/2020 à 18h43.
Sans questions il n'y a que des problèmes sans réponses.
Liet Kynes, exactement quelles sont tes motivations profondes quand tu essaye de comprendre la theorie des ensembles ?
Je pense que c'est avoir un support pour raisonner juste, savoir comment ne pas être en dehors de ce que je cherche à isoler lorsque je considère quelque chose.
Sans questions il n'y a que des problèmes sans réponses.
... aussi être en mesure de pouvoir continuer à échanger avec mon gamin, (il est en terminal, maths//physique/maths expert/HLP) sans lui dire trop de conneries.
Sans questions il n'y a que des problèmes sans réponses.
Alors ce n'est pas une motivation suffisante pour se mettre a etudier la theorie des ensembles. C'est pour cela que tu est toujours a cote de la plaque. Je te conseille fortement d'arreter car cela fait plusieurs mois que tu pretends vouloir etudier la theorie des ensembles et que tu tournes en boucle sur les meme petits bidouillages sans aucun interet pour le sujet, sans jamais vraiment demarrer serieusement. Tu ne comprends toujours pas en quoi consiste ZFC, et tu en est tres loin. Ce n'est pourtant pas mysterieux ni complique (au moins au debut), mais tu n;arrives pas a "accrocher". Laisse tomber, et va chercher reponse a comment raisonner juste ailleurs que dans ZFC ou la logique mathematique.
Si tu veux apprendre a raisonner juste fait plutot de la geometrie elementaire du college, ou lit les premiers livres des elements d'Euclide. Ca te sera surement plus profitable.
Ok, c'est au moins une réponse rassurante quant à mes préoccupations.
Sans questions il n'y a que des problèmes sans réponses.
En gros, tu étudies les bases de la philologie pour pouvoir aider ton gamin en grammaire ....
Et en plus tu comprends le vocabulaire de travers ...
Le conseil de Syborgg est bon.
Cordialement.
Bonjour , j'ai peut-être compris le principe. Si j'indexe aux ordinaux le nombre de sous ensembles des ensembles suivants :
0 {} : 0 sous ensemble
1 {{}} 1 sous ensemble
2 {{{}}} : 1 sous ensemble
3 {{{{}}}}: 1 sous ensemble
...
J’obtiens en dénombrant le nombre de sous ensembles de chaque ensemble, la suite 0,1,1,1,1,1... l'idée est-elle bien de considérer une formule unique qui permet de passer d'un index à l'autre? car si j'ai bien compris, la hiérarchie cumulative de Von Neumann utilise une seule formule qui permet que chaque ensemble possède pour éléments tout les ensembles précédents d'après https://fr.wikipedia.org/wiki/Axiome...hie_cumulative
Est-ce que je peux illustrer cela en disant que la schématisation ci dessous contient une formule unique pour les index de 0 à 2 puis une autre au passage de l'index 2 à 3 ?
Sans questions il n'y a que des problèmes sans réponses.
Mais apparemment ignoré. J'ai du mal à voir le lien entre des maths "relativement pointues" du XXème siècle et l'échange avec un élève de terminale qui ne va pas dépasser le XIXème et encore.
A priori, même s'il fait une fac de maths ou une prépa, la hiérarchie cumulative de von Neumann n'est pas ce sur quoi il va passer du temps ni même voir.
Quand à "raisonner juste", la 1ère des choses serait d'être méthodique et lucide et donc de ne pas s'attaquer dès le début à des choses trop difficiles, d'écouter ceux à qui on pose des questions et j'en passe. Mais cela a déjà été dit.
Donc au final la théorie des ensembles n'est accessible qu'avec des pré-requis ultra solides mais on l'utilise quasi dès le primaire. Je me souviens avoir fait des probas au lycée et l'on parlait d'ensembles aussi.
C'est souvent présenté comme une base pour raisonner. Puis quand je cherche à savoir de quoi il s'agit, je me rend compte que ce que je crois savoir est complétement faux, certains concepts utiles pour appliquer sur des problèmes concrets (surtout pour trouver des combinaisons, des probabilités) ont été adaptés d'un point de vue pragmatique.. bref ce que j'ai appris à l'école ce ne sont que des process.
Sans questions il n'y a que des problèmes sans réponses.
On peut aussi constater qu'il y a une différence entre les concepts élémentaires qu'on enseigne très tôt et s'attaquer à quelque chose de très formalisé conçu par Von Neumann qui volait assez haut.
Oui mais apprendre implique d'écouter ceux qui expliquent, pas de répéter ce qu'on croit savoir en boucle.
Il est évident que le problème est du coté de l'école en effet
Je me résout à intervenir à l'encontre de mes décisions : Vous mélangez théorie naïve, accessible en primaire, et les théories mathématiques accessibles bien plus tard.
C'est la même chose avec les opérations sur les entiers que l'on commence en CP et les théories axiomatiques de Peano que l'on doit voir en L3 voire M1
Je suis Charlie.
J'affirme péremptoirement que toute affirmation péremptoire est fausse
J'ai une formation technique (BTSA productions animales), le but de l'apprentissage n'était pas théorique mais pratique: savoir utiliser une méthode dans un but précis. Ce n'est pas une critique de l'école.Il est évident que le problème est du coté de l'école en effet
J'en suis conscient, les bases lorsque l'on a une progression non régulière dans l'apprentissage (étape par étape) sont le point de repère avec un retour permanent à celui ci lorsqu'une notion plus avancée est mal comprise. Il est difficile de raccrocher les wagons, c'est même contre productif si on a pas une continuité dans la démarche (travail régulier nécessaire mais pas forcement compatible avec le temps disponible dans la vie adulte ): on a parlait de Sysiphe il y a peu de temps.
Pour ce qui est de mon gamin, j'aurai aimé pouvoir être là quand il va aborder plus avant les maths, il m'a expliqué que le programme de cette année était vraiment plus intéressant,motivant et cela me fait plaisir, je trouve dommage de ne pas pouvoir être encore un peu à ces côtés pour partager pleinement son enthousiasme.
Sans questions il n'y a que des problèmes sans réponses.
Pour mieux connaître mon profil:
http://maths.btsa.free.fr/index.html voir en particulier dans: http://maths.btsa.free.fr/pages.php?choix=101
http://documents.irevues.inist.fr/bi...pdf?sequence=1
Sans questions il n'y a que des problèmes sans réponses.
pm42 : la construction des ordinaux de Von Neumann (ainsi que le fait que tout bon ordre est isomorphe a un seul ordinal de V.N.) est assez elementaire et facile a comprendre pour quelqu'un qui a un minimum de pratique mathematique. Je dirai qu'un bon eleve de terminale S pourrait tout a fait comprendre a digerer ceci, ou au moins un etudiant de premiere annee de maths. En fait ZFC est limpide et assez facile a comprendre jusqu'a un certain point, mais encore faut il avoir vraiment l'envie de s'y mettre. Les choses commence a se corser avec le forcing cependant...
Liet Keynes : pourquoi ne pas suivre mon conseil de faire plutot de la geometrie plane elementaire au niveau college/lycee, mais en t'efforcant de comprendre parfaitement les preuves et en faisant des tas d'exercices ? crois moi, ca te sera bien plus profitable !
Que les choses se compliquent avec le forcing je suis bien placé pour agréer (mon mémoire de master (comme on dirait aujourd'hui) portait sur le forcing avec un nouveau quantificateur), mais ZFC n'est pas aussi simple qu'il y paraît et c'est d'ailleurs un de ses pièges.
Je suis Charlie.
J'affirme péremptoirement que toute affirmation péremptoire est fausse
Je suis assez d'accord mais je pense que le primo-posteur n'a pas ce niveau justement et qu'il ne s'y prend pas du tout bien pour l'acquérir.
Mes remarques auraient été différentes avec quelqu'un qui ferait preuve de rigueur intellectuelle et qui serait capable d'écouter au lieu de s'acharner dans une voie sans issue.
Ceci dit, je pense que tu es optimiste sur "un bon élève de terminale S". J'ai l'impression que c'est plutôt abordable à un excellent élève qui est capable de prendre de l'avance sur le programme de 1ère année de fac/prépa.
D'où ce qu'ai écrit plus haut.
Le problème est que quand on ne comprend pas la théorie élémentaire des ensembles (disons celle de Cantor), c'est difficile de s'attaquer à une théorie formelle.
Le plus gênant, c'est qu'on considérait cette théorie élémentaire comme enseignable à des collégiens, et qu'on n'a pas vraiment besoin de plus pour aider un lycéen, voire un étudiant en licence. Encore faut-il accepter de lire les définitions comme elles sont et de ne se servir que des propriétés mathématiques pour faire des maths. Sans rajouter des baratins accessoires et trompeurs.
Cordialement.
Je precise mon propos : je parlais de ZFC jusqu'aux ordinaux, cardinaux, operations diverses et variees sur ces derniers, cardinaux reguliers, singuliers. Je pense qu'on sera d;accord pour dire que tout ceci est facile d'acces et limpide pour qui comprend et accepte "l'esprit" general de la theorie.
J'ai appris à me méfier du concept de "facile d'accès et limpide" : c'est peut-être le cas pour toi, pour Mediat et gg0. Je suppose que cela l'était aussi pour moi quand je faisais des études de maths.
Mais l'expérience montre qu'être à l'aise avec ce niveau d'abstraction nécessite pratiquement tout le temps la combinaison d'un esprit fait pour, d'une formation de bon niveau et pour l'avoir vécu, de ne pas perdre l'entrainement.
Je suis d'accord avec cela mais, je précise le mien : l'axiome des parties est mal compris généralement, le schéma d'axiomes de substitution n'est pas si évident, la distinction classe / ensemble peut poser quelques problèmes etc ...
Je suis Charlie.
J'affirme péremptoirement que toute affirmation péremptoire est fausse
C'est clair qu'on n'est pas tous "cablés" pareil, et certaines personnes ont beaucoup de mal à comprendre des choses qui paraissent évidentes à d'autres et les disparités individuelles existent pour tout les domaines qu'ils soient cognitifs ou physiques. Rien qu'à voir les (vrais) test de QI : ce qui est mesuré par ces tests est assez peu sensible à l'apprentissage, pourtant la variabilité inter-individuelle existe. Et m'est avis que quelqu'un avec 80 de QI aura beaucoup plus de mal (à effort équivalent) à faire des mathématiques que quelqu'un avec 120 de QI (sans jugement sur le reste de sa personne et dans les autres domaines).
Bref dans l'ensemble intelligence i si on a un cardinal limité on exprimera au plus card p(i) en conséquence et si le reste est à chercher dans les éléments du complémentaire de i inclus dans i cela risque pas de faire grand chose de plus
Sans questions il n'y a que des problèmes sans réponses.
Tu continues à enfiler comme des perles des mots de mathématiques ...
