DM Important Barycentres

[NathalieHi]

Bonsoir ,
Pour mercredi j'ai un DM assez important qui devrait me faire remonter ma moyenne .

Exercice 1
Construire en justifiant le barycentre des points pondérés A,-2 B,2 C,1

Alors moi je commencerais par cherche le barycentre de A et B que j'appelerai K

-2KA + 2KB = 0
-2KA + 2 ( KA + AB )
-2 KA + 2KA + 2AB
2AB = 0

Voila ou je bloque ? Ai je choisi les mauvais points pour trouvé un barycentre ? ...


Exercice 2

Construire en justifiant les centre d'inertie des plaques homogéne suivantes :




Pour la figure 1 il me semble qu'il fo la découpé en deux . Mais je n'en sait pas plus .... J'aurai vraiment besoin d'aide

Exercice n3

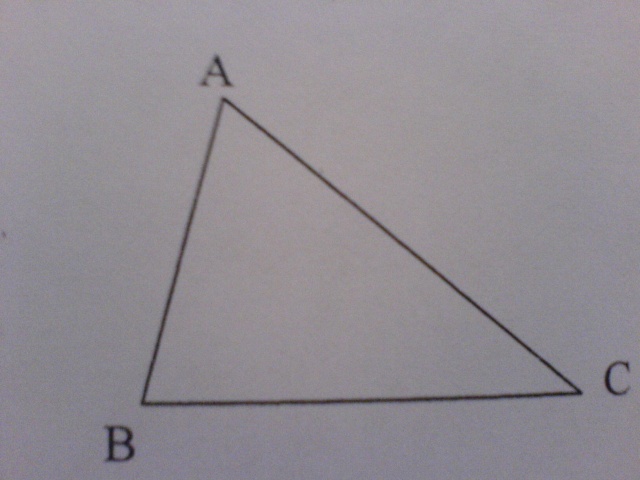
Soit ABC un triangle quelconque A'B'C' les poits définis par :
A' milieu de BC

AB' = 3/4 AC
BC' = 1/4 BA

K est le barycentre des points pondérés (A,1) ( B,3) (C,3 )

Placer les points A' B' C'



Je place donc B' a 3/4 de AC et C' a 1/4 de BA .

2) Determiner 3 réels m et n afin que B' soit le barycentre des points pondérés A,m et C,n

J'avoue avoir encore du mal j'aurais besoin d'une piste pour savoir comment commencer ? ...


Ce serait gentil de me donner au moins une piste

[Jeanpaul]

Pour le 1er : le barycentre n'existe que si la somme des poids ne vaut pas zéro ! Prends 2 autres points que A et B et ça ira mieux.

[Duke Alchemist]

Bonsoir.

Ex. 1 : voir ce qu'à indiqué JeanPaul.

Ex. 2 : Le centre de gravité est l'isobarycentre de tes isobarycentres
Tu détermines l'isobarycentre (centre de gravité) du rectangle puis celui du triangle et le centre de gravité recherché est au milieu...
Même principe pour la deuxième figure avec chacun des rectangles tu obtiens alors un triangle dont tu détermines le centre de gravité...

Ex. 3 : Il y a plusieurs manières d'arriver au résultat. En voici une :
- Exprime B' bar.{(A,m),(C,n)} sous forme vectorielle.
- Utilise le théorème de Chasles pour ne faire apparaître que les vecteurs AB' et AC
- Compare à l'énoncé et voilà.

Duke.

[homotopie]

Bonsoir,

Ex. 2 : Le centre de gravité est l'isobarycentre de tes isobarycentres
Tu détermines l'isobarycentre (centre de gravité) du rectangle puis celui du triangle et le centre de gravité recherché est au milieu...

Non, on prend l'isobarycentre (R) du rectangle et celui (T) du triangle (donc bien un dcoupage en 2 pièces). Isobarycentre car pièce homogène. Ensuite, on prend le barycentre de (R,surface du rectangle) (T, surface du triangle). Soit apparamment (R,2) (T,1)
Pour la pièce en 3 rectangles, on prend l'isobarycentre de l'isobarycentre car les 3 rectangles ont même aire (du moins apparamment).

pour le 3) nous sommes d'accord.

[hbenalia]

Bonsoir.

Ex. 2 : Le centre de gravité est l'isobarycentre de tes isobarycentres
Tu détermines l'isobarycentre (centre de gravité) du rectangle puis celui du triangle et le centre de gravité recherché est au milieu...
Même principe pour la deuxième figure avec chacun des rectangles tu obtiens alors un triangle dont tu détermines le centre de gravité...

Duke.

Bonjour à tout le monde.

Je tiens à préciser que l'isobarycentre du triangle sera affecté de 3 (somme des coefficients des trois sommets) et l'isobarycentre du carré sera affecté de 4 (somme des coefficients des quatre sommets) , et donc l'isobarycentre de l'ensemble ce n'est pas le milieu...
Et idem pour la deuxième figure...

Corrigez-moi si je me trompais...

Cordialement

[homotopie]

Bonjour à tout le monde.

Je tiens à préciser que l'isobarycentre du triangle sera affecté de 3 (somme des coefficients des trois sommets) et l'isobarycentre du carré sera affecté de 4 (somme des coefficients des quatre sommets) , et donc l'isobarycentre de l'ensemble ce n'est pas le milieu...
Et idem pour la deuxième figure...

Corrigez-moi si je me trompais...

Cordialement

Bonjour,
non !
Imaginons l'ensemble deux pièces ainsi constituées :
un triangle équilatéral ABC + un rectangle ABDE avec longueur du côté du triangle=1 mètre, deuxième côté du rectangle=1mm. Le centre de gravité de cet ensemble de pièces est très proche du centre de ABC. Avec tes coefficients hbenalia, le centre serait proche de [AB].
Tes coefficients correspondraient à l'isobarycentre des points d'un triangle et d'un rectangle vides et disjoints. (disjoint sinon certains points seraient affectés au total d'un coeff 2 et les autres d'un coeff 1=>n'est pas l'isobarycentre).
Cordialement

[Duke Alchemist]

Bonjour.

...
Ex. 2 : Le centre de gravité est l'isobarycentre de tes isobarycentres
Tu détermines l'isobarycentre (centre de gravité) du rectangle puis celui du triangle et le centre de gravité recherché est au milieu...

Bonsoir,


Non, on prend l'isobarycentre (R) du rectangle et celui (T) du triangle (donc bien un dcoupage en 2 pièces). Isobarycentre car pièce homogène. Ensuite, on prend le barycentre de (R,surface du rectangle) (T, surface du triangle). Soit apparamment (R,2) (T,1)...

Oh là là... Quelle horreur ai-je écrit là !!
Belle rectification homotopie
La prochaine fois, je réfléchirais un peu plus avant d'écrire n'importe quoi !

Duke.

[homotopie]

Oh là là... Quelle horreur ai-je écrit là !!

Je savais bien que c'était une erreur involontaire.