Bonjour,
Pour tout réel x, il existe un unique entier n tel que x compris entre n et n+1.
Cet entier est appelé la partie entière de x. Elle est notée E(x).
Par exemple, E(π) = 3 ; E(-3,5) = -4 ; E (2/3) = 0
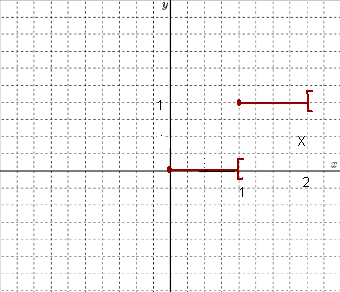
1. Vérifier que la fonction représentée est la fonction E(x)=x restreinte à l'intervalle [0;2]
(que veux dire restreinte deja?)
2.a. précisez E(1)
E(1)=1
b. La fonction E a-t-elle pour limite E(1) au point 1? autrement dit, pour tous les x voisins de 1, inférieurs à 1, les nombres E(x) viennent-ils s'accumuler en E(1)?
La fonction E n'a pas pour limite E(1) au point 1 car elle est discontinue.
3. tracez la courbe représntative de la fonction E restreinte à l'intervalle [0;5[
a. En quels point de [0;5[ la fonction E est-elle discontinue?
b. La fonction E est-elle continue sur l'intervalle ]3;5[ ?
4. Quelle es l'image de l'intervalle I= [0;2[ par la fonction E? E(I) est-il un intervalle?
Moi je pense que vu que la fonction est discontinue sur [0;2[ on ne peut pas définir un intervalle exact E(I) puisque le point 0 a par exemple plusieurs antécédent, et le point 1 aussi, mais ca ne forme pas pour autant un intervalle. C'est les deux seules solutions possibles.
5. Quelle es l'image de R par la fonction carrée? de l'intervalle ]moins l'infini; 2]?
L'image de R est R
L'image de l'intervalle]mois l'infini; 2] est ] Plus l'infini; 4]
Pouvez vous me corriger les questions aux quelles j'ai répondu, et m'aider à terminer les autres questions?
-----