Angles orienté

[invitef07c4cf3]

Bonjour à tous

Je viens de commencer le chapitre sur les angles orienté et voici un exo que j'ai à faire en activité.
Pouvez vous m'expliquer sur quel piste chercher pour le résoudre

Voici l'exo:

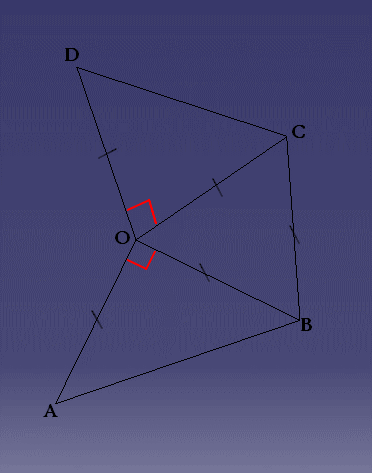
A partir de la figure ci-contre, pour chacun des angles orientés suivants :
- Trouvez la mesure de l’angle géométrique associé
- Donnez sa mesure principale.
a/ (OA,OC)
b/ (OA,OD)
c/ (CB,OC)
d/ (OB,DO)
e/ (BA, CB)
f/ (DC, BC)

Il s'agit de vecteur je n'est pas mis les fléches.
J'ai essaye de refaire la figure, c'est pas tout à faire exact mais j'ai anoté


Merci d'avance de me guider.
-----

[VegeTal]

Quel est ton problème ? Si tu as du mal tu peux chercher la mesure des angles géométriques puis les mettre en orientés.

Par exemple tu fais une translation du vecteur (le point O devient C) . Le triangle OCB est équilatéral donc chaque angle vaut 60°, ° ; Ici on tourne bien dans le sens inverse des aiguilles d'une montre d'où .

[invitef07c4cf3]

Ok mais par exemple pour (BA, CB) comment faire car on a pas toute les mesures

[bourbaki]

A propos d'une mesure de l'angle (BA, CB) ...


bonjour,

tu peux utiliser la relation de Chasles.
Exprime la mesure de l'angle (BA, CB) en fonction de celles des angles dont tu peux déterminer les mesures (utilise les cotés des triangles qui contiennent le point B ...). Tu vois comment faire ?

Ensuite, quel est le lien entre les mesures des angles (BO, CB) et (BO,BC) (résultat très utile dans cet exo) ?

[A voir en vidéo sur Futura]

[invitef07c4cf3]

Désolé mais je ne comprend pas :s

Le probleme c'est que je n'ai pas un angle du type ABC à calculer mais (AB,AC) Je ne comprend pas pourquoi c'est avec des vecteurs,
Déja si j'arrive à comprrendre ça j'arriverais mieux l'exo

[bourbaki]

justement,
ce qu'il te manque c'est la notion d'angles orientés de vecteurs, tu n'as pas compris ce que ça représente visiblement.
Le plus simple est de regarder sur ton livre de cours comment ça se présente, le lien avec les angles géométriques etc. , ou sinon sur Google.

exemple:
https://formation.cfai-centre.net/wi...s/vecteurs.pdf

Ensuite je pense tu pourras aborder ton exercice beaucoup plus sereinement


A dans 15 min

[bourbaki]

Quel est ton problème ? Si tu as du mal tu peux chercher la mesure des angles géométriques puis les mettre en orientés.

Par exemple tu fais une translation du vecteur (le point O devient C) . Le triangle OCB est équilatéral donc chaque angle vaut 60°, ° ; Ici on tourne bien dans le sens inverse des aiguilles d'une montre d'où .

autre méthode (plus simple et plus propre je pense):
on sait que (cours) : Dans le plan, pour tous vecteurs et , on a : (ça se voit clairement sur un dessin)
Donc

[VegeTal]

je voulais pas faire de passes passes, si déjà il n'a pas très compris.

[bourbaki]

je me permets de citer un mathématicien connu des étudiants, on ne "cultive" pas le brouillon pour la raison simple que ... ce n'est pas lui qui sera noté! *


*: Dany-Jack Mercier

[invitef07c4cf3]

pour le 4/ je dirais donc 5pi/6 + pi = 6pi/6 = pi

Non??

[bourbaki]

je ne crois pas non, pourrait-on voir ta démonstration pour comprendre ensemble ton raisonnement ?

[invitef07c4cf3]

90° pour DOC + 60° pour COB (triangle équilatéral) = 150°

pi/2 + pi/3 + pi= 6pi/6

[bourbaki]

faut que tu arrives à réfléchir et écrire ceci en termes d'angles orientés de vecteurs, à utiliser les angles en radians sinon tu vas te planter. tu peux réécrire stp ...

[invitef07c4cf3]

b) 8pi/6
c) 2pi/3

Pour toutes les autres je n'arrive pas .... Ce chapitre me semble vraiment difficiles :s

[bourbaki]

restons au d) si tu veux bien, ce serait bien de comprendre comment ça marche ...

tu cherches une mesure de l'angle
Pour celà, voilà comment réfléchir (à lire avec des guillemets !!!) :
tu cherches à mesurer l'angle entre les vecteurs et , pour cela tu pars de , et tu "tournes" dans le sens direct jusqu'à "arriver à" . tu as (avec la relation de Chasles) .
Problème, on ne sait pas mesurer l'angle car les vecteurs qui forment cet angle n'ont pas même origine. On utilise la relation

Est ce que tout ceci t'aide à comprendre comment ça marche, essaie de résoudre le petit d en m'expliquant comment tu fais stp ?

[invitef07c4cf3]

(OB,OC) = PI / 3
(OC,OD) = PI / 2
(OC,DO) = - PI/2 + PI

(OB,DO) = PI/3 - 2PI/2 = -1PI/6

Je Doute vraiment pour la dernier à cause du moin :s

[bourbaki]

effectivement, ça merdouille quand tu passes de (OC,OD) à (OC,DO).
En fait, (OC,OD) = PI / 2 du coup (OC,DO) = PI/2 + PI , et ceci vaut 3PI /2

En conclusion, (OB,DO) = PI/3 +3PI/2 = 2PI/6 + 9PI/6=11PI/6.
une autre mesure de (OB,DO) est 11PI/6 - 2PI, soit -PI/6, mais je ne vois pas comment tu arrives à ce résultat, tes calculs st faux
l'égalité PI/3 - 2PI/2 = -1PI/6 est fausse et en plus, d'où sort le -2PI/2 ?

[invitef07c4cf3]

Mon -2PI /2 Venais de -PI/2 + PI ... Merci de m'avoir corriger.

Pour le e/ je dirais que c'est la meme maniere que le d/ car doit mettre BC à la place de CB.

BA/BO = PI/2
BO/ BC = PI/3
BO/CB= PI/3 +PI

DOnc BA/CB= PI/2+ PI/3+PI = 3PI/6 + 2PI/6+ 6PI/6= 11PI/6

[bourbaki]

Mon -2PI /2 Venais de -PI/2 + PI ... Merci de m'avoir corriger.

Pour le e/ je dirais que c'est la meme maniere que le d/ car doit mettre BC à la place de CB.

BA/BO = PI/2
BO/ BC = PI/3
BO/CB= PI/3 +PI

DOnc BA/CB= PI/2+ PI/3+PI = 3PI/6 + 2PI/6+ 6PI/6= 11PI/6

attention aux abus de notations, je veux bien tolérer (BA,BO) pour désigner \widehat{(\vec{BA}, \vec{BO} )}, d'ailleurs je l'utilise ... , mais bon, écrire BA/BO je t'avoue que ça me fait mal aux yeux, doucement quand même ...

Ton raisonnement me paraît tout à fait correct, attention quand même à la précipitation, l'égalité (BA,BO)= PI/2 est fausse ! ... du coup ton calcul est faux. Une autre faute aussi, ce sont des angles dits orientés de vecteurs, la mesure de l'angle (BO,BC) est égale à -PI/3, l'angle géométrique est bien de PI/3 mais en le mesurant de BO à BC dans le sens indirect ... (j'espere que c'est clair)
Mais bon, j'ai l'impression que ça rentre, c est cool

[invitef07c4cf3]

Pourquoi (BA,BO) n'est pas égal à Pi/2?

[bourbaki]

Pourquoi (BA,BO) n'est pas égal à Pi/2?

C'est (OA,OB) qui mesure PI/2 dans le triangle OAB.

D'apres la figure, le triangle OAB est isocèle (direct même). Du coup, les angles à la base sont de même mesure, c'est à dire (AB,AO)=(BO,BA), et puisque la somme des mesures des angles dans un triangle est égale à 2PI, on trouve, apres calculs (à développer) que (BA,BO)=-PI/4

NB: je suis patient, mais toutefois j'aimerais vraiment que tu bosses le cours, en particulier les paragraphes 2)B, 2)C le tout le paragraphe 3) du lien suivant: https://formation.cfai-centre.net/wi...s/vecteurs.pdf. Sans ça, tu ne t'en sortiras pas

[bourbaki]

et puisque la somme des mesures des angles dans un triangle est égale à 2PI

j'ai écrit n'importe quoi ... c'est égal à PI bien sûr ...

[invitef07c4cf3]

(BA,BO) = - PI/4
(BO, BC) = -PI/3
(BO,CB)= - PI/3 +PI

DOnc BA/CB= -PI/4 - PI/3 +PI = -3-4+12PI/12 = 5PI/12

Je vais bien réviser le cours