Fonctions.

[invite61a47ef5]

Bonjour,comme vous pouvez le voir j'ai répondu à la premiere question bon j'en suis pas vraiment fière,j'arrive pas à répondre au autre question et sa serait gentil si quelqu'un acceptait de m'aidé s'il vous plait (pas de me donné les réponses...).Merci d'avance.
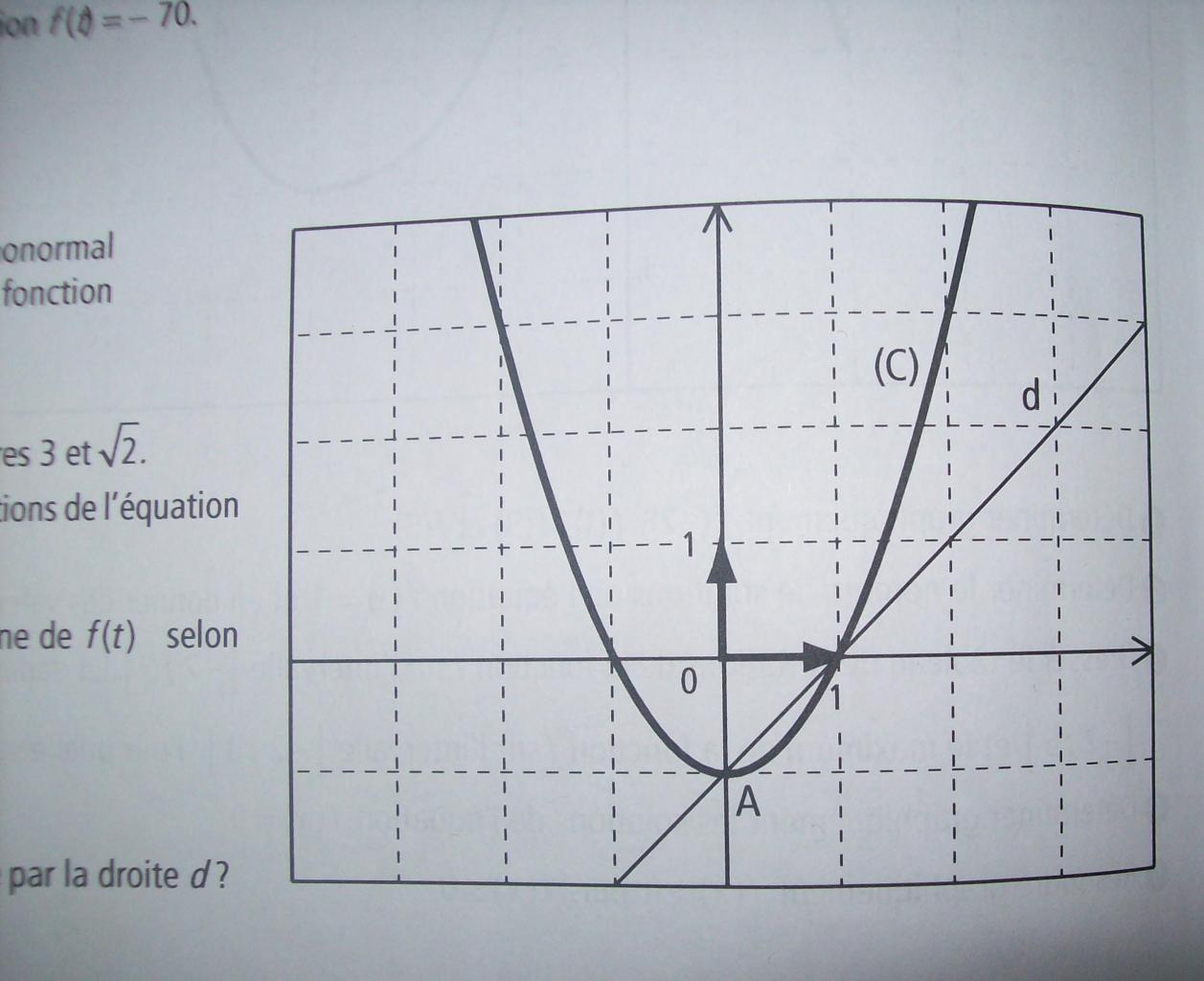
La courbe (C) ci-contre dans le repère orthonormal ( 0;i;j), est la courbe représentative de la fonction f définie sur par f(t)=t²-1.
1)a)Déterminer les images par f des nombres 3 et racine carré2
Réponse:f(3)=3²-1=9-1=8
f(racine carré2)=(racine carré2)²-1=2-1=1
b)Déterminer les valeurs exactes des solutions de l'équation f(t)=5.
Réponse: f(t)=5 <=> t²-1=5
<=> t²=6
<=> t=racine carrée 6 ou t= -racine carrée6.

2)Indiquer de deux façons différentes le signe de f(t) selon les valeurs de t:
a)graphiquement
b)par le calcul

3)Quelle est la fonction affine g représentée par la droite d ?

4)Résoudre l'inéquation f(t)g(t):
a)graphiquement
b)par le calcul

Pour le graphique:

-----

[inviteae7fd42d]

Bonjour,

pour la question 2)a) il faut que tu lises sur le graphique les valeurs de t pour lesquelles f(t) est par exemple negatif (indice: tu obtiens un intervalle) puis pour lesquelles f(t) est positif (deux intervalles).

2)b) il te faut resoudre une inequation:

et tu trouve l'encadrement de t correspondant (ca recoupe la reponse de la question precedente), idem pour f(t)>0...

3) la fonction g est une fonction affine, son equation est donc de la forme g(x)=ax+b
A toi de determiner les valeurs de a et b en prenant des valeurs particulieres de x, en lisant par exemple sur le graphe g(0)=-1 ca te permet de trouve b=..? ensuite tu prends une autre valeur pour determiner a, ok?

4) resoudre l'inequation f(t)g(t) >0? (la fin de la question manque..)
a) le produit des deux fonctions est positif lorsque:
-soit: f(t)>0 et g(t)>0. a toi de trouver les valeurs convenant en lisant sur le graphe
-soit: f(t)<0 et g(t)<0. pareil

b) on procede de la meme facon par le calcul:

deux systemes d'inequations a resoudre..

[Flyingsquirrel]

Bonjour,

@svt18 : J'ai mis le graphiques en pièce jointe. Merci de lire ce fil et d'éviter d'héberger tes images sur des serveurs extérieurs à chaque fois que cela est possible.

Pour la modération, Flyingsquirrel.

[invite61a47ef5]

d'accord flyingsquirrel

[A voir en vidéo sur Futura]

[invite61a47ef5]

merci niconico d'avoir répondu;
"pour la question 2)a) il faut que tu lises sur le graphique les valeurs de t pour lesquelles f(t) est par exemple negatif (indice: tu obtiens un intervalle) puis pour lesquelles f(t) est positif (deux intervalles)."

les valeurs de t pour lesquelles f(t) est par negatif :[0;-2,4]
les valeurs de t pour lesquelles f(t) est positif:[0;2,2]??

je pense pas que ce soit les bonnes réponses...

[invite61a47ef5]

2)b)b) t²-1>=0 <=> t²>=1
<=> t appartient à ]-oo, -1] U [1,+oo[.

t²-1<0 <=> t appartient à ] -1,1[.

[Duke Alchemist]

Bonjour.

2)b)b) t²-1>=0 <=> t²>=1
<=> t appartient à ]-oo, -1] U [1,+oo[.

t²-1<0 <=> t appartient à ] -1,1[.

C'est OK

les valeurs de t pour lesquelles f(t) est par negatif :[0;-2,4]
les valeurs de t pour lesquelles f(t) est positif:[0;2,2]??

je pense pas que ce soit les bonnes réponses...

Comment as-tu trouvé les réponses en gras ci-dessus ?
f(t) est négatif quand sa courbe représentative est sous l'axe des abscisses c'est-à-dire quand x ...

Même raisonnement pour f(t) positif...

Il serait bien que tu trouves les mêmes réponses qu'à la résolution par le calcul.

Duke.

[invite61a47ef5]

Bonjour,
les valeurs de t pour lesquelles f(t) est par negatif :]-oo;-1]
les valeurs de t pour lesquelles f(t) est positif:[1;+00[??

[invite61a47ef5]

c'est faux ???

[invite61a47ef5]

pour la4) c'etait 4) resoudre l'inequation f(t)< (supérieur ou égal comme je peux pas mettre le trait en dessous du signe)g(t)

[inviteae7fd42d]

pour la question 4), il faut que tu cherches sur le graphique les valeurs de t (sur l'axe des abscisses) pour lesquelles le graphe de f est en dessous du graphe de g (si l'inequation est ).
Tu trouves donc l'intervalle...?

Ensuite on te demande de resoudre par le calcul:

Bien entendu, tu dois retomber sur les memes reponses que ce que tu as trouve graphiquement...

Pour en revenir a la question 2), les valeurs de f(t) sont a lire sur l'axe des ordonnees. Donc f(t)<0 quand sa courbe representative est en dessous de l'axe des abscisses. Tu lis alors les valeurs de t correspondantes sur l'axe des abscisses.
On trouve bien f(t)<0 pour t appartenant a ]-1,1[, non?

[inviteae7fd42d]

Bonjour,
les valeurs de t pour lesquelles f(t) est par negatif :]-oo;-1]
les valeurs de t pour lesquelles f(t) est positif:[1;+00[??

cette reponse n'est pas correcte... Note bien par contre que les reponses que tu as trouve par le calcul sont correctes..

[invite61a47ef5]

je prends en compte tout ce que tu as dit donc je reste sur la question 2)a) donc sa devrait donné ça..

[invite61a47ef5]

Bonjour.C'est OK

Comment as-tu trouvé les réponses en gras ci-dessus ?
f(t) est négatif quand sa courbe représentative est sous l'axe des abscisses c'est-à-dire quand x ...

Même raisonnement pour f(t) positif...

Il serait bien que tu trouves les mêmes réponses qu'à la résolution par le calcul.

Duke.

les valeurs de t pour lesquelles f(t) est positif:]-oo;-1]U[1;+oo[
les valeurs de t pour lesquelles f(t) est négatif:] -1,1[.

[invite61a47ef5]

je me perds,je suis meme pas sur d'avoir bien compris..

[invite61a47ef5]

je me sens un peu perdu alors je vais essayé de rectifié et de savoir si on est d'accord,donc on me demande d'indiquer de deux façons différentes le signe de f(t) selon les valeurs de t graphiquement et par le calcul
donc graphiquement la premiere facon c'est :
f(t) = (t - 1)(t + 1):

t ------------------ -oo ------------- (-1) ------------------ (1) ------------- +oo
t - 1 ---------------------- ( - ) ----------------- ( - ) ----- 0 ------ ( + ) ----
t + 1---------------------- ( - ) ------ 0 ------- ( + ) -------------- ( + ) ----
(t - 1)(t + 1) ----------- ( + ) ----- 0 ------- ( - ) ------ 0 ----- ( + ) -----

ensuite la deuxième c'est comme on l'a dit plus haut
:les valeurs de t pour lesquelles f(t) est positif:]-oo;-1]U[1;+oo[
les valeurs de t pour lesquelles f(t) est négatif:] -1,1[.

[Duke Alchemist]

Bonjour.

Graphiquement c'est sans l'étude du tableau de signe !

En regardant la courbe, il est clair que :
- la courbe est au-dessus de l'axe des abscisses pour les abscisses inférieures à -1 => f(t) > 0
- la courbe est en-dessous de l'axe des abscisses pour les abscisses comprises entre -1 et 1 => f(t) < 0
- la courbe est au-dessus de l'axe des abscisses pour les abscisses supérieures à 1 => f(t) > 0

Voilà ce qu'on te demande.
Et tu es bien d'accord que c'est ce que tu retrouves par le calcul.

Duke.

[invite61a47ef5]

d'accord donc graphiquement ça donne "- la courbe est au-dessus de l'axe des abscisses pour les abscisses inférieures à -1 => f(t) > 0
- la courbe est en-dessous de l'axe des abscisses pour les abscisses comprises entre -1 et 1 => f(t) < 0
- la courbe est au-dessus de l'axe des abscisses pour les abscisses supérieures à 1 => f(t) > 0"comme vous avez dit et par le calcul :t²-1>=0 <=> t²>=1
<=> t appartient à ]-oo, -1] U [1,+oo[.

t²-1<0 <=> t appartient à ] -1,1[.

f(t)=t²-1.
f(t) = (t - 1)(t + 1):

t ------------------ -oo ------------- (-1) ------------------ (1) ------------- +oo
t - 1 ---------------------- ( - ) ----------------- ( - ) ----- 0 ------ ( + ) ----
t + 1---------------------- ( - ) ------ 0 ------- ( + ) -------------- ( + ) ----
(t - 1)(t + 1) ----------- ( + ) ----- 0 ------- ( - ) ------ 0 ----- ( + ) ----- ?

[invite61a47ef5]

passons..j'en ai finit avec la question 2),par contre j'ai bien lu ce que niconico a dit pour la question 3) mais j'ai pas vraiment compris le procédé à suivre..

[invite61a47ef5]

"3) la fonction g est une fonction affine, son equation est donc de la forme g(x)=ax+b
A toi de determiner les valeurs de a et b en prenant des valeurs particulieres de x, en lisant par exemple sur le graphe g(0)=-1 ca te permet de trouve b=..? ensuite tu prends une autre valeur pour determiner a, ok?"

[hhh86]

Cela implique que tu as un système à résoudre :
Le points A(-1;0) appartient à d donc ses coordonnées vérifient l'équation de d
g(-1)=0<=>-a+b=0
Le points de coordonnées (0;1) appartient à d donc ses coordonnées vérifient l'équation de d
g(0)=1<=>b=1

[invite61a47ef5]

je suis pas sur d'avoir compris mais alors ça donnerait g(0)=-1 donc b=-1
g(1)=-1donc a=-1??

[hhh86]

Cela implique que tu as un système à résoudre :
Le points A(-1;0) appartient à d donc ses coordonnées vérifient l'équation de d
g(-1)=0<=>-a+b=0
Le points de coordonnées (0;1) appartient à d donc ses coordonnées vérifient l'équation de d
g(0)=1<=>b=1

Je t'ai marqué n'importe quoi

A(0;-1) appartient à d
g(0)=-1<=>b=-1
Le point de coordonnées (1;0) appartient à d
g(1)=0<=>a+b=0<=>a-1=0<=>a=1

De toutes façons tu vois facilement que la pente de ta droite est 1 et que son ordonnée à l'origine est -1

[invite61a47ef5]

pour moi a=1 et b=-1 mais je saurais pas le justifier..

[invite61a47ef5]

désolé j'avais pas vu ce que tu avais écrit.

[invite61a47ef5]

je parle de ce que tu viens d'écrire..

[invite61a47ef5]

merci je viens de comprendre

[invite61a47ef5]

pour la question 4 j'ai un peu de probleme à résoudre l'inéquation graphiquement meme si j'ai bien compris qu'il faut trouver un intervalle ,quelqu'un pourrait m'aider s'il vous plait ?

[hhh86]

f(t)g(t)>0
<=>f(t)>0 et g(t)>0 ou f(t)<0 et g(t)<0
<=>(t appartient à ]-inf;-1[U]1;+inf[ et t appartient à ]1;+inf[) ou (t appartient à ]-1;1[ et t appartient à ]-inf;1[)
<=>(t appartient à ]1;+inf[) ou (t appartient à ]-1;1[)
<=>t appartient à ]-1;+inf[

[invite61a47ef5]

j'ai passer un détail ,désolé..c'est f(t)<(ou egal)g(t)