TS : intégrale [ln(x)]^n dx

[invite356611b8]

Bonsoir,
je dois effectuer une intégration par parties, je voulais savoir comment on doit procéder lorsque l'on a une puissance? Ici [ln(x)]^n dx
Dois-je poser u(x)=1 v(x)=[ln(x)]^n ?

Merci
-----

[Kley]

bonjour.

Bonsoir,
je dois effectuer une intégration par parties, je voulais savoir comment on doit procéder lorsque l'on a une puissance? Ici [ln(x)]^n dx
Dois-je poser u(x)=1 v(x)=[ln(x)]^n ?

Merci

C'est u'(x)=1.

[invite356611b8]

Oui (petite inattention), le problème c'est qu'en posant :
u'(x) = 1
v(x)= [ln(x)]^n
on a : u(x) = x
v'(x) = (n/x)*[ln(x)]^(n-1) ?
donc je me retrouve a nouveau avec du ln(x) lors de mon I.P.P ce qui pose problème puisque l'on ne connaît pas de primitive de ln...
J'ai sans doute fait une erreur, pouvez-vous m'éclairer?

Merci

[Coincoin]

Salut,
Une IPP te permet de trouver une relation de récurrence entre n et n-1.

[A voir en vidéo sur Futura]

[invite356611b8]

Je crois avoir compris, il faut que j'exprime Un en fonction de Un-1, puisque mon intégrale va de 1 à e, si je ne me trompe pas, je trouve :
Un = e-n*U(n-1).
Mais le but de cette IPP était de démontrer que la suite U est croissante et positive, donc j'ai pensé à calculer la différence : Un+1 - Un mais je ne crois pas que cela m'avance...

Merci de votre aide

[Coincoin]

Plutôt que la différence, regarde le rapport. Est-ce que le facteur permettant de passer de Un-1 à Un est plus grand que 1 ? Pour le signe, il faut une récurrence : est-ce que si Un-1>0 alors Un>0 ? est-ce que U0>0 ?

[MyL38]

Bonjour,

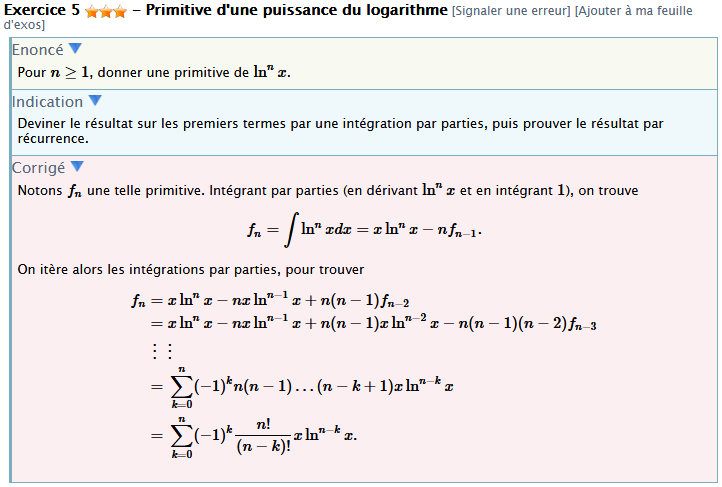
Sur un site de maths, j'ai retrouvé cet exercice, sauf que là, il s'agit de trouver une primitive de cette fonction.
Sur l'image ci dessous, il y'a le corrigé.
Seulement même avec le corrigé, je ne comprends pas très bien comment ils arrivent à passer de l'étape des IPP à l'étape d'après (là ou les k apparaissent).
Parce que je me disais en voyant le (n-k+1).x.ln(x)^(n-k) à l'avant dernière ligne, comment on sait qu'on doit arrêter le calcul lorsque k=n ?
Je dis ça parce que le calcul des IPP nous demande éternellement de refaire une nouvelle IPP, donc comment se fait-il qu'à l'avant dernière ligne, on ne se retrouve pas avec une étape supplémentaire comme (n-k).x.ln(x)^(n-k-1).. et ainsi de suite ?? Vous voyez ?

Même si j'ai vérifié leur résultat final avec la primitive de ln(x) et ça marche (quand on dérive on revient bien sur ln(x)). Mais je ne comprends pas la démarche pour établir ces lois, je n'arrive pas à les établir moi-même.

Est-ce que quelqu'un pourrait m'expliquer plus en détails ?

Merci

[jacknicklaus]

comment on sait qu'on doit arrêter le calcul lorsque k=n ?

Bonjour,

Le dernier terme est en f_n-k donc celà nécessite k <= n car f_-1 n'a pas de sens. Le nombre total de termes est déterminé par ce k, il est donc fini :
k = 1 --> 2 termes
k = 2 --> 3 termes
k = n (le max) --> n+1 termes (de 0 à n)

De plus, le passage "avec les k" utilise implicitement, pour le dernier terme où k = n, le fait que f₀ = x, en tant qu'une primitive de 1.

[Black Jack 2]

Bonjour,

Sur un site de maths, j'ai retrouvé cet exercice, sauf que là, il s'agit de trouver une primitive de cette fonction.
Sur l'image ci dessous, il y'a le corrigé.
Seulement même avec le corrigé, je ne comprends pas très bien comment ils arrivent à passer de l'étape des IPP à l'étape d'après (là ou les k apparaissent).
Parce que je me disais en voyant le (n-k+1).x.ln(x)^(n-k) à l'avant dernière ligne, comment on sait qu'on doit arrêter le calcul lorsque k=n ?
Je dis ça parce que le calcul des IPP nous demande éternellement de refaire une nouvelle IPP, donc comment se fait-il qu'à l'avant dernière ligne, on ne se retrouve pas avec une étape supplémentaire comme (n-k).x.ln(x)^(n-k-1).. et ainsi de suite ?? Vous voyez ?

Même si j'ai vérifié leur résultat final avec la primitive de ln(x) et ça marche (quand on dérive on revient bien sur ln(x)). Mais je ne comprends pas la démarche pour établir ces lois, je n'arrive pas à les établir moi-même.

Est-ce que quelqu'un pourrait m'expliquer plus en détails ?

Merci

Pièce jointe 419801

Bonjour,



Poser :
u = ln^n(x) = --> du = n.(ln(x))^(n-1) * 1/x dx
dv = dx ---> v = x

S u dv = u.v - S v du
S ln^n(x) dx = x.ln^n(x) - S n.(ln(x))^(n-1) dx
S ln^n(x) dx = x.ln^n(x) - n.S (ln(x))^(n-1) dx

Et donc