Bonjour à tou(te)s,
Voici le sujet :
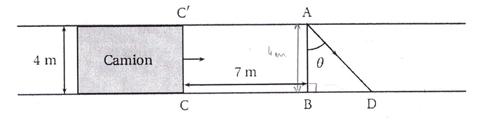
Un lapin désire traverser une route de 4 mètres de largeur. Un camion, occupant toute la largeur de la route, arrive à sa rencontre à la vitesse de 60 km/h. Le lapin décide au dernier moment de traverser, alors que le camion n'est plus qu'à 7 mètres de lui. Son démarrage est foudroyant et on suppose qu'il effectue la traversée en ligne droite au maximum de ses possibilités, c'est-à-dire à... 30 km/h !
L'avant du camion est représenté par le segment [CC'] sur le schéma du premier post. Le lapin part du point A en direction de D. Cette direction est repérée par l'angle x=BAD avec 0 inférieur ou égale x inférieur ou égal à pi/2.
1) On admet que le triangle ABD est rectangle en B. Déterminer les distances AB et CD en fonction de x.
2) En déduire les temps t1 et t2 mis par le lapin et le camion pour parcourir respectivement les distances AD et CD.
3) On pose f(x)=7/2+2tan(x)-4/cos(x)
4)a) On appelle f' la fonction dérivée de f. Déterminer f'(x).
b) Etudier les variations de la fonction f sur [0;pi/2[
c) Montrer que f admet un maximum sur [0;pi/2[. Déterminer la valeur exacte de ce maximum.
d) Remplir le tableau.
e) Construire la courbe représentative de la fonction f sur l'intervalle [0;1] dans un repère orthonormé (O;i;j). On choisira 1 cm pour 0,1.
5) On constate sur le graphique précédent que l'équation f(x)=0 admet 2 solutions. On va rechercher une valeur arrondie au centième de chacune d'elle.
a) Montrer que l'équation f(x)=0 est équivalente à l'équation : 7cos(x)+4sin(x)-8=0
b) Montrer que, pour x € [0;pi/2[, cette équation est aussi équivalente à l'équation : 65sin²(x)-64sin(x)+15=0
c) Résoudre l'équation ci-dessus et en déduire les valeurs arrondies au centième des solutions de l'équation f(x)=0.
6) La lapin survivra-t-il s'il démarre avec un angle de :
a)15° ? b)30° ? c) 45° ?
Je pense avoir bon pour les question 1, 2, 4a, 4b (peut-être pas complète), 4d, 5a. Mises à part ces questions, j'ai beaucoup de mal à trouver des solutions...
Voilà mes réponses (je remplace la lettre teta par x, pour plus de facilité à transcrire) :
1) AD=4/cos(x) en utilisant la trigonométrie
BD=4tan(x)+4 à l'aide de la trigonométrie également
2) t1=12/25cos(x) en utilisant la formule t=d/v
t2=(12tan(x)+21)/50 avec t=d/v également
3) Pas réussie. J'imagine que je dois soustraire t1 à t2 et que je dois tomber sur mais je n'y parviens pas.
4) a) Je trouve f'(x)=(2-4sin(x))/cos²(x)
b) Je cherche la valeur pour laquelle 2-4sin(x)=0 puisque cos²(x) est forcément positif, le signe ne dépend que de 2-4sin(x). Et donc après calcul je trouve x=pi/6
Le tableau de signes et variations donne donc : f'(x) positif entre 0 et x=pi/6 et négatif entre x=pi/6 et x=pi/2 donc croissant de 0 à x=pi/6 et décroissant de x=pi/6 à x=pi/2
c) J'imagine que l'extremum est mais je ne sais pas comment le montrer.
d) x| 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 |
f(x)|-0.5| -0.5 |-0.49|-0.49|-0.49|-0.48|-0.48|-0.48|-0.47|-0.47|-0.47|
e) Je ne sais pas dans que mettre en abscisse et en ordonnée, et si on utilise 1cm pour 0.1, le résultat me parait improbable...
5) a) 7/2+2tan(x)-4/cos(x)=0
7/2+2tan(x)=4/cos(x)
7+4tan(x)=8/cos(x)
7+4*(sin(x)/cos(x))=8/cos(x)
7+4sin(x)=8
7+4sin(x)-8=0
b) Aucune idée de la méthode.
c) 65sin²(x)-64sin(x)+15=0
delta=64²-4*65*15
=196
x1=(64-14)/130=0.38
x2=(64+14)/130=0.6
Pas sûr sûr pour cette question.. est-ce que les solutions sin(x)1 et sin(x)2 ou alors x1 et x2 ?
6) Que faire ?
J'espère que vous pourrez m'aider, merci d'avance.
-----