Le problème qui résiste à mes premières S!
Je vous propose de voir si vous avez les mêmes
difficultés que mes première S sur un exercice tout simple!
Bon courage!
Voilà l'énoncé:
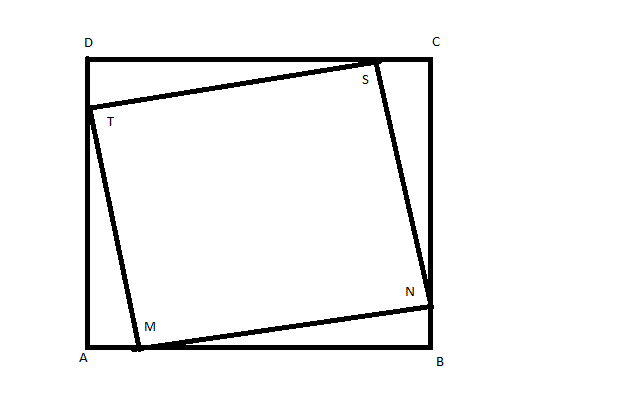
ABCD est un carré de côté 10cm. Les points M, N, S et T appartiennent respectivement aux segments [AB], [BC], [CD] et [DA] et sont tels que AM = BN = CS = DT.
Ou placer M pour que le quadrilatère MNST
- ait un périmètre maximal?
- ait un périmètre minimal?
Bonjour,
Instinctivement, pour le périmètre maximal je place M en A. Pour un périmètre mini, je place M au milieu de [AB].
Sinon, pour faire plus propre : soit x=AM. soit a=AB=10. On calcule TM grâce à Pythagore. Puis une étude de fonction sur [0;10] me permet de trouver le minimum et le maximum de TM.
"Quand le calcul est en contradiction avec l'intuition, je refais le calcul"
Je suis d'accord avec Titiou mais je vais détailler la démonstration.
Cliquez pour afficher
Bonjour
La symetrie du problème implique que le quadrilatère MNST est aussi un carré
Si AM = x et le coté du grand carré est a , le carré du coté de MNST est (a -X)² + X²
On cherche les extremum ceux ci sont donnés par -a +2x = 0 d'à_ X= a/2
En science " Toute proposition est approximativement vraie " ( Pascal Engel)
Les élèves étant malins et prêts à tout pour obtenir une solution toute cuite, il me paraît souhaitable de vérifier le statut de ce nouvel inscrit avant de lui donner une solution détaillée. D’ailleurs, la règle qui consiste à donner des pistes et non des solutions complètes s’applique dans tous les cas, non ?
Bonne idée, au vu de la simplicité du problème, il est probable que ce petit malin a trouvé un pseudo trompeur pour recueillir des solutions complètes.Envoyé par DSCH
La présentation est très astucieuse, nous le reverrons peut-être bientôt ?
Comprendre c'est être capable de faire.
Bonjour,
étant sonné que j' ai bientôt un test, je m' entraine à faire cet exercice. ( Il est dans mon livre). En effet, je suis votre démarche pour essayer de comprendre mais je ne vois pas à quel mesure correspond la lettre d pour la fonction dérivée d' un polynôme.
Merci d' avance pour votre réponse
En revoir.
Ce n'est pas une mesure, juste une notation pour dire qu'on dérive par rapport à la variable x. En gros:
par contre je trouve que vous faites compliqué.
surface d'un triangle =base*hauteur/2
donc si x =AM
le triangle étant rectangle S(TMA)=x(10-x)/2
on a 4 triangles identiques à retirer de la surface totale
surface cherchée =100-2x(10-x)
l dérvée vaut si 0
2*10-4x = 0 soit x=5 pour une surface max
la surface min valnt bien sur pour x=0
Merci beaucoup, parce que je ne comprenais pas.
En revoir.
Bonjour,
Le "d" sert uniquement à noter la dérivée de f.
Si j'ai utilisé cette notation c'est parce que je préfère éviter de confondre les objets mathématiques. Si f est une fonction, f(x) est une expression. Une expression est l'évaluation d'une fonction en une variable, ce n'est pas une fonction.
Je considère que l'opérateur "prime" permet de parler de la dérivée d'une fonction. Ainsi f' est la fonction dérivée de f. Il y a tout de même des liens forts entre la fonction f et l'expression f(x) et si f est dérivable on peut dire que f(x) est dérivable par rapport à x.
La dérivée d'une fonction peut être donné indépendamment du nom qu'on donne a son argument, ce n'est pas vrai pour une expression et c'est pour ça que je préfère éviter d'écrire [f(x)]'. L'opérateur d/dx permet de préciser par rapport à quoi on dérive.
Bien sûr je ne fais pas une syncope si je vois écris [f(x)]' et je conçois qu'on puisse par abus de langage étendre l'opérateur "prime" aux expressions pour parler de leur dérivée quand ce n'est pas ambiguë, mais je préfère moi-même éviter.
Ah non, là je ne suis pas d'accord.En gros:
Tu peux nous donner la définition d'une fonction dérivable sans recourir à f(x) ? Honnêtement, c'est de la masturbation intellectuelle car il n'y a que les algébristes pour faire la distinction entre f et f(x).
Vous n'écrirez pas quelque chose comme f=3x+2. Vous faites la distinction entre une fonction et un nombre et dans de nombreux cas si vous ne le faisiez pas vous vous retrouveriez avec des aberrations.
Dans le cas de la dérivation d'expression, si on considère la fonction fa : x -> ax². Ecrire fa'(x)=2ax ne prête a aucune confusion. Mais si on veut dériver l'expression on écrit [ax²]' et là je ne sais plus si je suis en train de dériver par rapport à x ou par rapport à a.
Dans le premier message je devais dériver la fonction p². Entre le carré de la dérivée et la dérivée du carré, je préférais avoir une notation un peu lourde plutôt qu'une notation illisible (bien que non-ambiguë si on est d'accord sur sa lecture).
Je comprend qu'on puisse argumenter en faveur d'écrire des abus de langage, mais je ne comprend pas qu'on puisse refuser de reconnaître que c'en est. On ne justifie pas en maths qu'on écrive des choses ouvertement fausses sous prétexte qu'on se moque du fait que ce n'est pas vrai.
Bien sûr, il suffit d'utiliser f(y). Pourquoi appeler "x" l'argument ? Mais plaisanteries mises de cotés, je pense pouvoir vous définir f' sans faire appel a l'expression de f.Tu peux nous donner la définition d'une fonction dérivable sans recourir à f(x) ?
f' est la fonction qui a un point associe le nombre dérivé de f en ce point. Ce nombre dérivé est le coefficient directeur de la tangente au graphe de f au point considéré.
Je n'ai pas fait appel à l'expression de f et la définition n'est pas ambiguë. Même si ce n'est pas forcément très pratique pour faire des calculs ^^.
Je ne dis pas qu'il n'y a pas de lien entre fonctions et expressions, mais ça reste des objets différents et il est important d'un point de vue pédagogique de faire la part des choses, sans nécessairement appuyer dessus outre mesure. Imaginez par exemple que la personne a qui vous enseignez ait envie de devenir algébriste
Quoi qu'il en soit, vous ne me ferez pas écrire des choses volontairement fausses sous prétexte... sous quel prétexte au fait ?
P.S : Je ne suis pas algébriste, je suis logicien et je connais pas mal d'analystes qui font la distinction entre une fonction et son expression. Comme je l'ai dit, pas de quoi en faire une syncope, mais savoir de quoi il s'agit et éviter d'écrire des choses qui n'ont pas de sens, il y a pas mal de domaines en mathématiques où ça a son importance.
Mon message était en réaction à ceci:
Ce qui signifiait qu'il existait une définition "f est dérivable" et une autre définition pour "f(x) est dérivable par rapport à x", que ces définitions étaient indépendantes et que l'une impliquait l'autre. En analyse, on fait plutôt la distinction entre la différentielle (df et dx, deux applications) et la dérivée de f en x (f'(x), un nombre) et on montre que différentiable <=> dérivable. Ce qui donne: df = f'(x)dx (application = nombre x application), d'où le df/dx = f'(x).si f est dérivable on peut dire que f(x) est dérivable par rapport à x
Raté: elle se cache dans le terme "coefficient directeur".f' est la fonction qui a un point associe le nombre dérivé de f en ce point. Ce nombre dérivé est le coefficient directeur de la tangente au graphe de f au point considéré. Je n'ai pas fait appel à l'expression de f
En sup certainement, en prépa peut-être, mais certainement pas en secondaire.Je ne dis pas qu'il n'y a pas de lien entre fonctions et expressions, mais ça reste des objets différents et il est important d'un point de vue pédagogique de faire la part des choses, sans nécessairement appuyer dessus outre mesure.
Ça explique tout.Je ne suis pas algébriste, je suis logicienLe problème de la rigueur absolue, c'est que sans abus de notations on ne fait rien.
Dernière modification par Bruno ; 05/11/2011 à 19h00.
Yep, on peut définir indépendamment qu'une fonction f et qu'une expression f(x) sont dérivables (dans le deuxième cas en précisant toutefois par rapport à quoi on dérive).
A partir de là on peut démontrer un théorème qui affirme que si f(x) est l'expression associée à la fonction f alors f est dérivable si et seulement si f(x) est dérivable par rapport à x.
Même en définissant la dérivabilité de f a partir de celle de f(x) (par rapport à x). Ça reste des objets différents et on a besoin de deux définitions de la dérivabilité pour chacun de ces deux objets.
Formellement si vous simplifiez par dx vous devriez écrire df/dx=f'(x)Id, comment le rapport de deux applications pourrait-il donner un réel, on ne change pas d'algèbre ?En analyse, on fait plutôt la distinction entre la différentielle (df et dx, deux applications) et la dérivée de f en x (f'(x), un nombre) et on montre que différentiable <=> dérivable. Ce qui donne: df = f'(x)dx (application = nombre x application), d'où le df/dx = f'(x).
Bien sûr, même moi je ne vais pas jusqu'à un tel niveau de diptérosodomie (ou est ce de la drosophilie ?). Mais je trouve tout aussi rapide et élégant de déduire de df=f'(x)dx que (df/dx)(x)=f'(x).
Non non, le coefficient directeur est un objet. On peut évidemment lui associer son expression qu'on calcul à l'aide de f(x). Mais il existe bien une fonction qui à une droite affine du plan associe son coefficient directeur dans la base canonique.Raté: elle se cache dans le terme "coefficient directeur".
A mon avis c'est une grave erreur. Je ne pense pas qu'il soit souhaitable d'enseigner à nos chère tête blondes le plus de confusions possibles pour ensuite avoir l'occasion de leur faire faire la part des choses. Appuyer dessus outre mesure serait stupide, mais c'est pas plus mal si le prof évite de faire des confusions lui-même et s'il introduit des notations dont ses étudiants pourront se resservir même lorsqu'ils auront compris ce qu'elles signifient.En sup certainement, en prépa peut-être, mais certainement pas en secondaire.
Je ne l'ai jamais nié, bien au contraire. Evidemment qu'il faut faire des abus de notations pour faire des maths. Je parle de cet abus en particulier. Qu'est-ce qu'il apporte ?Ça explique tout.
De la concision ? Dans certains cas oui, dans au moins autant de cas c'est plus rapide de ne pas le faire.
De la clarté ? Absolument pas, une expression un peu compliquée avec des "primes" partout, c'est illisible.
Une meilleurs visualisation du concept ? Non, c'est même contre-productif de ce point de vu.
En plus de ça c'est générateur de confusions, d’ambiguïtés et ça peut être source d'erreurs. Je ne vois décidément pas le moindre intérêt à écrire "prime" après une expression (dûment mise entre crochets) pour signifier qu'on la dérive. Ça ne me gêne pas que des gens le fasses, mais je ne le ferais pas sans une bonne raison.
Ce qui conduit à perdre l'indépendance des définitions, et c'est ce qui se passe dans l'histoire du coefficient directeur.
Merci de relever cet abus de notation, qui en est bien un dans ce cas.Formellement si vous simplifiez par dx vous devriez écrire df/dx=f'(x)Id, comment le rapport de deux applications pourrait-il donner un réel, on ne change pas d'algèbre ?
Ça ne sert à rien s'ils continueront à noter par la suite df/dx = f'(x) = f' (la dernière étant bizarre, le x disparaissant) car in fine ce qui compte c'est le sens physique, sauf peut-être pour le logicien. Il existe des abus de notation bien plus dangereux, comme celui consistant à écrire f(x,y) puis f(r, theta) au lieu de f(r*cos theta, r*sintheta) qui peut conduire à x=r et y=theta !A mon avis c'est une grave erreur. Je ne pense pas qu'il soit souhaitable d'enseigner à nos chère tête blondes le plus de confusions possibles pour ensuite avoir l'occasion de leur faire faire la part des choses. Appuyer dessus outre mesure serait stupide, mais c'est pas plus mal si le prof évite de faire des confusions lui-même et s'il introduit des notations dont ses étudiants pourront se resservir même lorsqu'ils auront compris ce qu'elles signifient.
Lesquelles ? Qu'apporte en plus le respect des notations, si ce n'est de la confusion ?En plus de ça c'est générateur de confusions, d’ambiguïtés et ça peut être source d'erreurs.
Éliminer des sources d'erreurs et d'incompréhension ?
J'avais compris, mais il y aurait un exemple de cas pathologique ? Personnellement, je n'en ai jamais rencontre.
Je parlais de dy/dx=f'(x) par rapport à dx/dx = f'...
Le fait que deux propositions soient équivalentes signifient qu'elles sont vraies simultanément, mais pas qu'il s'agit de la même proposition.
En fait c'est celui du milieu qui me semble bizarre. Effectivement ça ne sert à rien si in fine ils notent ça. Mais le but que je poursuis c'est que justement ils n'écrivent pas ça in fine.Ça ne sert à rien s'ils continueront à noter par la suite df/dx = f'(x) = f' (la dernière étant bizarre, le x disparaissant)
Je suis bien d'accord. Il y a toujours pire, dans ce cas précis je note parfois aussi avec un tilde la fonction dont les arguments sont en coordonnés polaires.Il existe des abus de notation bien plus dangereux, comme celui consistant à écrire f(x,y) puis f(r, theta) au lieu de f(r*cos theta, r*sintheta) qui peut conduire à x=r et y=theta !
Que signifie [ax²]' ? Et vous n'allez pas me faire croire que ce genre de notation n'arrive jamais, sous prétexte que quelque chose ressemble à une constante on ne s'en préoccupe plus.Lesquelles ? Qu'apporte en plus le respect des notations, si ce n'est de la confusion ?
De plus la notation ne peut pas se généraliser aux cas d'expressions de plusieurs variables. Je trouve ça pratique d'avoir des notations qui se généralisent, surtout quand elles n'ont pas vraiment d'inconvénients ^^.
Je dis que c'est sources d'erreurs parce que, je ne sais pas vous, mais une expression un peu compliquée avec des "primes" partout je trouve ça illisible et c'est super dur de calculer dedans. La notation n'étant pas plus concise car il faut de toutes façons mettre des crochets partout.
Sérieusement, vous ne m'avez pas encore donné un seul avantage à l'emploie de cette notation. Tout ce que vous me dites c'est que ce n'est pas la peine de ne pas faire l'abus de langage. Mais quelle peine y a-t-il a ne pas le faire ? Pourquoi faudrait-il le faire ?
P.S : Je me suis un peu laissé emporté, ce n'est pas vraiment un abus de langage dans les cas très limités ou elle n'est pas ambiguë on peut très bien dire qu'on note [f(x)]' la dérivée de l'expression f(x). Simplement cette notation ne se généralise pas, elle impose de devoir préciser que tout ce qui intervient dans l'expression autre que x lui-même est bien une constante et bien souvent noter simplement f'(x) est bien plus léger.
Sans doute une erreur «par abus de notation» (le dans ce cas étant implicite dans le post) qui a introduit la confusion
Soit.
Comme tu le dis, ça te semble bizarre. A première vue, avoir un dx qui apparait dans le membre de gauche sans un x dans le membre de droite choque plus que le rapport de deux applications.En fait c'est celui du milieu qui me semble bizarre. Effectivement ça ne sert à rien si in fine ils notent ça. Mais le but que je poursuis c'est que justement ils n'écrivent pas ça in fine.
Et tu ne me feras pas croire qu'un [ax²]' sort souvent de nulle part sans qu'on ait dit précisément de quoi on parle (ce qui est la moindre des choses en mathsQue signifie [ax²]' ? Et vous n'allez pas me faire croire que ce genre de notation n'arrive jamais, sous prétexte que quelque chose ressemble à une constante on ne s'en préoccupe plus.).
Tout à fait d'accord mais c'est hors de propos dans un forum "Mathématiques du collège et du lycée".De plus la notation ne peut pas se généraliser aux cas d'expressions de plusieurs variables.
Un avantage: ne pas utiliser une notion inconnue en lycée et ne pas trainer des quotients partout lorsqu'on calcule. Sinon, je pensais que le débat tournait autour de df/dx=f'(x) vs df/dx=f' et pas prime vs d/dx ?Sérieusement, vous ne m'avez pas encore donné un seul avantage à l'emploie de cette notation.
Non, juste une faute de frappeSans doute une erreur «par abus de notation» (le dans ce cas étant implicite dans le post) qui a introduit la confusion
C'est inutile de passer du temps à l'expliquer aux élèves, ils ont d'autres choses à faire. Mais je ne vois pas pourquoi se priver de leur apprendre des notations dont ils pourront se resservir.
D'autant que leur apprendre d'autres notations ne fait qu'une différence, a savoir qu'ils ne pourront pas s'en resservir.
Comme je l'ai dit, écrire df/dx=f'(x) est faux. Ce n'est pas un abus de notation, c'est une erreur, vous dites qu'une fonction est égale à un nombre. Vous pouvez écrireUn avantage: ne pas utiliser une notion inconnue en lycée et ne pas trainer des quotients partout lorsqu'on calcule. Sinon, je pensais que le débat tournait autour de df/dx=f'(x) vs df/dx=f' et pas prime vs d/dx ?
Vous avez plein de notations qui sont correctes. Pourquoi s'acharner à choisir la seule qui soit fausse ? Qu'est ce qu'elle apporte ?*
De plus je ne suis pas en train de débattre autour de prime vs d/dx. Je suis en train de dire que c'est abus et qu'il n'est jamais nécessaire d'utiliser "prime" pour dériver une expression.
Ecrire quelque chose comme [f(x)]' est un abus qui n'apporte rien. On peut très bien écrire à la place
Le premier cas évite des crochets un peu partout dans l'expression et a l'avantage de mettre l'opérateur avant l'opérande ce que je trouve personnellement beaucoup plus pratique pour calculer.
Le deuxième cas (f'(x)) permet une notation beaucoup plus légère, mais il faut avoir la fonction a disposition (ce qui n'est pas une grande peine à introduire).
Pourquoi donc vouloir utiliser une notation plus lourde, moins lisible et qui devient fausse dés qu'on tente de généraliser ? L'argument que vous avancez en sa faveur c'est que ça aide à mieux confondre deux notions distinctes (mais proches).
Décidément je ne vois pas comment on peut faire l'apologie de la confusion en mathématiques
*Vous remarquerez que je vous pose toujours la même question et que vous n'y répondez jamais. Quel est l'intérêt de ces abus de langage ? Pourquoi faire un abus de langage alors que de ne pas le faire ne coûte rien ?
Je pensais avoir été clair dans mon message précédent: df/dx=f'(x) est bien un abus de notation, tu le trouveras dans de nombreux ouvrages comme celui-ci: http://books.google.fr/books?id=LnBU...page&q&f=false ou http://books.google.fr/books?id=wLEW...nction&f=false
df/dx=f' est certes plus correct que =f'(x) mais ambigu sur les variables de f, et après tout rien ne nous empêche de définir df et dx comme des quantités et non des applications.
Quant à la préférence de f'(x) par rapport à [f(x)]', je suis d'accord mais je ne vois pas le rapport. Toujours est-il qu'on a largement dévié de la question initiale et que df/dx=f'(x) était suffisamment explicite pour la personne qui ne connaissait pas et ne méritait certainement pas tout ce foin.
bonjour , pouvez vous , me donner la solution j'ai essayer mais je ne suis pas arriver
merci d'avance!
comment trouves tu dx?
