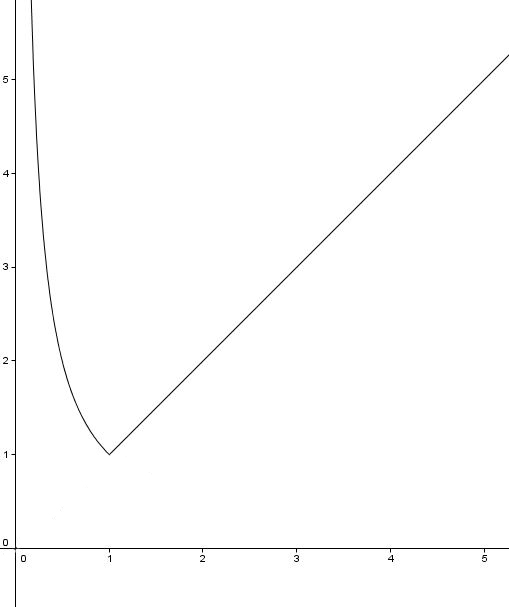
Est ce que cette fonction est dérivable en 1 ?
Discussions similaires
-
Par invitebd9321df dans le forum Dépannage
Réponses: 5
Dernier message: 13/07/2009, 15h51
-
Par invite7174db88 dans le forum Mathématiques du supérieur
Réponses: 7
Dernier message: 19/10/2008, 16h58
-
Par thomas5701 dans le forum Mathématiques du supérieur
Réponses: 5
Dernier message: 21/03/2008, 21h25
-
Par invite0c5534f5 dans le forum Mathématiques du collège et du lycée
Réponses: 7
Dernier message: 28/02/2008, 21h30
-
Par invite9f60ab2b dans le forum Chimie
Réponses: 5
Dernier message: 12/02/2006, 16h16