Problème d'oreiller (boules blanches et noires) de Lewis Carroll !!!

[benpotter]

Bonjour, j'ai ce problème à résoudre. Pouvez-vous m'aider?

Un problème d’oreiller (Pillow Problem) de Charles Dodgson, alias Lewis Caroll.
Un sac contient initialement une seule boule dont on sait qu’elle est soit blanche, soit noire.
On met une boule blanche dans le sac et on mélange.
On tire alors une boule au hasard : elle est blanche. Quelle est la probabilité que la boule restant dans le sac soit blanche ?

Au début, je pense logiquement que la proba est de 1/2. Mais sur certains sites anglais, je trouve 2/3.
Ils affirment qu'on a soit
tiré la boule blanche 2 et donc on tire ensuite la boule blanche 1 (qui aurait pu être noire)
soit
tiré la boule blanche 2 et donc on tire ensuite la boule noire 1 (qui aurait pu être blanche)
soit
tiré la boule blanche 1(celle qui aurait pû être noire) et donc ensuite on tire obligatoirement blanche 2 ce qui nous fait 2/3.

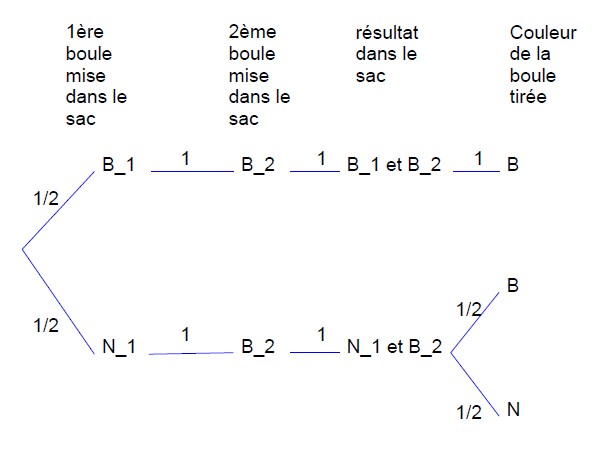
Comment peut-on matérialiser cela avec un arbre pondéré ?...
De plus, j'hésite encore...
-----

[louisdark]

Il y a 1 chance sur deux qu'il y ai deux boules blanches, 1/2 chances qu'il y ait une boule noire et une boule blanche.
Tu as tiré une boule blanche, il y a donc 1/2 chance qu'il y ait une noire, 1/2 pour une blanche

[benpotter]

Faux. Il y a 2/3 ^^

[louisdark]

.... Tu fais les questions et les réponses?

[A voir en vidéo sur Futura]

[zyket]

Bonjour,

On tire alors une boule au hasard : elle est blanche. Quelle est la probabilité que la boule restant dans le sac soit blanche ?

Et si l'on transforme l'énoncé par : On tire alors une boule au hasard : elle est noire. Quelle est la probabilité que la boule restant dans le sac soit blanche ?

[louisdark]

Selon mon raisonnement, encore 1 chance sur 2

[zyket]

Ben moi je dirai que la proba que la boule restante soit blanche est de 1. Ou dit autrement si je tire une boule noire en fait j'ai tiré l'unique boule noire donc je suis certain que les boules restantes sont blanches, non ?

[louisdark]

Ah oui, une erreur de raisonnment merci

[RuBisCO]

Pour répondre à la question posée, il faut donc considérer le problème : le sac contient initialement la boule 1, on rajoute la boule 2 blanche.

notations utilisées
Soit l'évènement "choisir la boule n"
l'évènement "la boule est noire"
l'évènement "la boule est blanche".

mise en situation
étape 1 : je tire au hasard une boule : j'ai une chance sur deux de choisir la boule 1, autant de choisir la boule 2.

A ce stade, on a et .

étape 2 : je m'intéresse maintenant à la couleur : la boule 1 est soit noire, soit blanche. Pour la boule 2, elle est toujours blanche.

Ainsi, on obtient les probabilités conditionnelles suivantes : , , et

Maintenant, on fait l'arbre de probabilité correspondant :

Et là, j'obtient la conclusion suivante :

et , ce qui n'est pas ce que vous proposez ! Donc où est l'erreur ?

[louisdark]

Ainsi, on obtient les probabilités conditionnelles suivantes : , , et

Petite erreur, de frappe probablement :
et , il faut faire une multiplication et non une somme

[RuBisCO]

J'ai peur de ne pas avoir tout saisi...

[RuBisCO]

Zut, double post regrettable mais il le faut : j'ai vu l'erreur dont tu parles, évidement c'est

et !
Cela m'apprendra à faire des maths à 4 heures du matin !

[louisdark]

Moi aussi j'ai fait une faute de frappe :
et

[RuBisCO]

En tout cas, je n'ai pas de trace de 2/3, c'est surtout ça que je voulais faire remarquer.

[zyket]

Bonjour,

Pièce jointe supprimée

je propose un autre schéma qui me semble équivalent à celui proposé par RuBisCo. Et j'arrive à la même conclusion la proba de tirer une boule blanche à la fin du processus est de p(B)=(1/2*1*1*1)+(1/2*1*1*1/2)=3/4
et la probabilité de tirer une boule noire est de p(N)=(1/2*1*1*1/2)=1/4

[zyket]

Je refais le post avec une image et non pas un fichier pdf comme illustration





je propose un autre schéma qui me semble équivalent à celui proposé par RuBisCo.

B_1 est une boule blanche mise à la première étape ; N_1 est une boule noire mise à la première étape

B_2 est la boule blanche mise à la deuxième étape

Et j'arrive à la même conclusion la proba de tirer une boule blanche à la fin du processus est de p(B)=(1/2*1*1*1)+(1/2*1*1*1/2)=3/4
et la probabilité de tirer une boule noire est de p(N)=(1/2*1*1*1/2)=1/4

Que vaut ce raisonnement ?