Différence courbe exponentielle et logarithmique

[invitefa49eb69]

Bonjour à tous,

J'ai une petite question au sujet de la distinction entre courbe exponentielle et logarithmique dans le cadre de la datation absolue par désintégration radioactive.

Je pensais (à tort a priori) que les courbes exponentielles étaient forcément décroissantes, au contraire des courbes logarithmiques, croissantes.
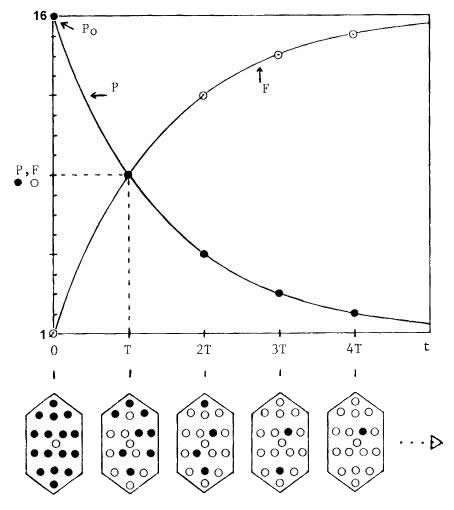
Pouvez-vous m'expliquer pourquoi, parmi les 2 courbes ci-dessous, la courbe croissante est logarithmique et la courbe décroissante exponentielle ? Quel argument a-t-on sachant que ce n'est pas toujours le cas ?

Merci beaucoup pour votre réponse, sachant que mes cours de maths pures commencent à dater !

Bon 1er mai !
-----

[invitefa49eb69]

Forcément, c'est mieux avec le graphique...

[zyket]

Bonjour,

la courbe exponentielle est du type Ce^(kx) avec C réel strictement positif, la dérivée de cette fonction est Cke^(kx) et quelque soit x réel on sait que e^x>0 donc Cke^(kx) est du signe de k puisque C>0.

Conclusion :
- si k<0 alors la courbe est décroissante.
- si k>0 alors la courbe est croissante.

[invitefa49eb69]

Merci pour votre réponse,

Du coup, sachant que l'on observe une décroissance par désintégration de l'éléments-père, k<0 (comme il y a perte d'éléments) et donc la courbe exponentielle est décroissante, c'est cela ?

Qu'en est-il pour la courbe logarithmique ? Comme il s'agit là d'une apparition d'éléments-fils, on a k>0 et donc courbe positive ?

Mais dans ce cas, d'où vient le choix entre courbe logarithmique et exponentielle sachant que les 2 peuvent avoir la même allure ?

Merci encore pour votre aide

[A voir en vidéo sur Futura]

[zyket]

Il ne s'agit pas d'un choix

Le résultat de la courbe exponentielle décroissante vient de la résolution de l'équation différentielle y'=k.y, qui en français se traduit par : la vitesse de désintégration est proportionnelle à la quantité d'éléments radioactifs.

Explications :
Mathématiquement la quantité d'éléments radioactifs est représentée par la variable y. Cette variable y est fonction du temps, on peut donc écrire y=f(t) (En français : y est la quantité d'éléments radioactifs à l'instant t). On note f ' la fonction dérivée de la fonction f .
f '(t) représente la vitesse de désintégration à l'instant t.

L'expérience physique montre que la vitesse de désintégration à chaque instant t est proportionnelle à la quantité d'éléments radioactifs présents à cet instant t. On peut donc écrire f '(t)=k.y, avec k réel

Or y peut aussi s'écrire f(t) d'où f '(t)=k.f (t) ce qui en français se traduit par : la vitesse de désintégration à l'instant t est proportionnelle à la quantité d'éléments radioactifs à l'instant t. (ici le facteur de proportionnalité est le nombre k)

Mathématiquement f '(t)=k.f (t) s'appelle une équation différentielle. Pour plus de commodité on choisit de noter y' le nombre dérivé f '(t), on peut donc écrire y'=f '(t) et y=f(t) d'où l'écriture classique d'une équation différentielle y'=k.y

On sait que la solution d'une telle équation différentielle, y'=k.y, est une fonction f telle que f(t)=C . e^(k.t)
D'après les données de ton graphique on peut déterminer les constantes C et k de cette fonction f.

Pour t=0 on a f(t)=P_0=16 , d'où d'après f(t)=C . e^(k.t) on a donc C . e^(k.0)=16 or e^(k.0)=1 d'où C=16
La fonction f est donc du type f(t)=16.e^(k.t)

On voit sur le graphique qu'à l'instant T, qui correspond à l'instant où la quantité d'éléments radioactifs est la moitié de la quantité initiale P_0, on a f(T)=1/2 . 16=8
On a donc 16.e^(k.T)=8 d'où e^(k.T)=1/2 d'où k.T=ln(1/2) d'où k= - ln(2)/T

Donc grâce aux données expérimentales du graphique on peut écrire l'évolution de la quantité, y, d'éléments radioactifs au cours du temps par la fonction : y=f(t)=16.e^((- ln(2)/T).t)

Remarque : la courbe croissante n'est pas une courbe logarithmique. Une courbe logarithmique en fonction du temps tend vers -infini lorsque t tend vers 0, or ici il existe une valeur pour t=0.
Cette courbe croissante a une équation du type g(t)=C . e^(k.t) + b
Car on a f(t)+g(t)=16, la somme de la quantité, f(t), d'éléments radioactifs à chaque instant t et de la quantité, g(t), d'éléments issus de la désintégration est égale à la somme de ces éléments à l'instant t=0

d'où ici g(t)=16-16.e^((- ln(2)/T).t)

P.S.
J'espère que je n'aurais pas écrit trop de bêtises

[invitefa49eb69]

Merci pour la précision de la réponse !

Du coup, si j'ai bien compris , les 2 courbes sont exponentielles en fait ?? Tout dépend du signe de la constante k ?

[zyket]

Oui les deux courbes sont exponentielles.

Maintenant l'allure des courbes exponentielles dépend des constantes C et k

Rappels :

- la fonction Exp telle que Exp(x)=e^x est une fonction définie sur R. Elle est strictement croissante. (e^x)>0 pour tout réel x, donc sa courbe représentative est constamment au dessus de l'axe des abscisses, celui-ci (l'axe des abscisses) est asymptote horizontale en - l'infini. Cette courbe passe par les points (0;1) et (1;e)

- la fonction f telle que f(x)=-Exp(x)=-e^x est une fonction définie sur R. Elle est strictement décroissante. (-e^x)<0 pour tout réel x, donc sa courbe représentative est constamment au dessous de l'axe des abscisses, celui-ci (l'axe des abscisses) est asymptote horizontale en - l'infini. Cette courbe passe par les points (0;-1) et (1;-e)

- une fonction g telle que g(x)=e^(k.x) est une fonction définie sur R. Elle est strictement croissante pour k>0, elle est strictement décroissante pour k<0. (e^(k.x))>0 pour tout réel x, donc sa courbe représentative est constamment au dessus de l'axe des abscisses, celui-ci (l'axe des abscisses) est asymptote horizontale en - l'infini pour k>0 et asymptote horizontale en + l'infini pour k<0

- une fonction h telle que h(x)=C.e^(k.x) est une fonction définie sur R. Elle est strictement croissante pour (C>0 et k>0) ou pour (C<0 et k<0) donc pour C et k de même signe. Elle est strictement décroissante pour (C>0 et k<0) ou pour (C<0 et k>0) donc pour C et k de signe contraire. Dans tous les cas sa courbe représentative passe par les points (0;C) et (1;C.e^k)
Sa courbe représentative est constamment au dessus de l'axe des abscisses si C est positif quelque soit k.
Sa courbe représentative est constamment au dessous de l'axe des abscisses si C est négatif quelque soit k.

[invitefa49eb69]

Super, je crois avoir bien compris, merci beaucoup !!!