Bonjour
Dans le triangle en photo, je doit trouver la valeur de 'a' à partir des données présentes.
J'ai essayé de trouver un maximum de valeurs possible, ou du moins d'écrire les inconnues à partir d'autres inconnus mais je n'arrive à rien.
Auriez vous des pistes à me donner pour y arriver ?
On est en plein dans les produits scalaires mais je ne vois pas quoi utiliser pour y arriver.
merci !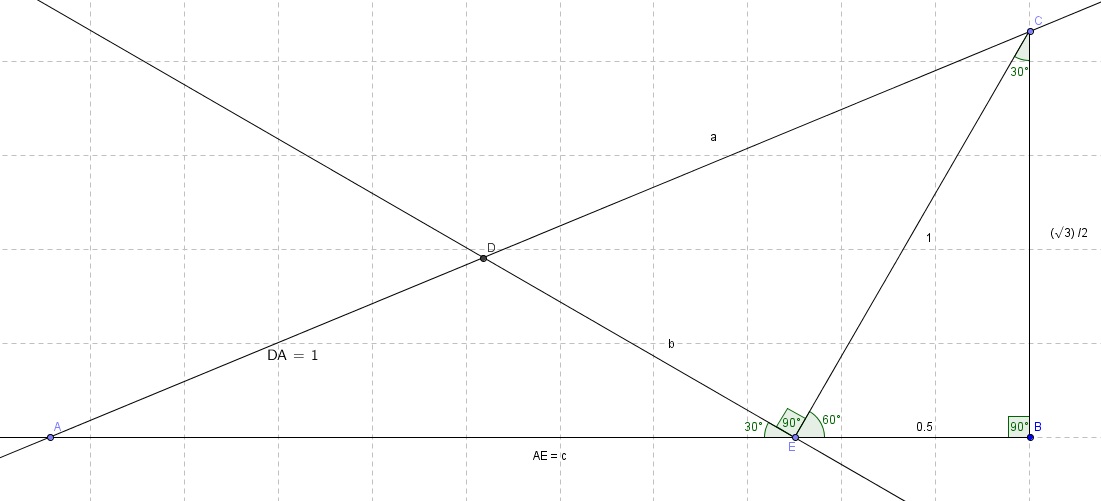
Bonjour.
En regardant comment faire la construction, on voit qu'il y a une solution unique (ce qui ne veut pas dire qu'elle soit facilement calculable).
ma première idée a été d'utiliser les triangles CED et BAC, puis la formule d'Al Kashi dans le triangle AED (DA²=...).
Cela donne un système de trois équations à trois inconnues pas très sympa.
D'où une autre idée : utiliser un repère d'origine B et dont les axes sont sur les côtés du triangle BAC. Il est facile de trouver l'équation de ED, puis on imposerait DA=1.
Comme c'est ton exercice, je te laisse chercher. A moins que tu aies eu une indication.
Cordialement.
Je tente de t'orienter, bien que je ne suis qu'en 1S, et que j'ai commencé les produits scalaires que cette année. x)
- Dans le triangle ABC, tu peux trouver une équation où tu as 2 inconnues, a et c. ---> Pythagore
- Dans le triangle ACE, même chose. ---> Al-Kashi
Ça te fera un système de deux équations à deux inconnues, compliqué, certes, mais ça, tu sais le résoudre !
En espérant de pas m'être planté, bonne chance.
J'ai essayé avec un système à 3 équations, et après plusieurs page de calculs ça me mène nul part.
gg0, considères-tu ED comme un vecteur, en utilisant un repère ?
Effectivement,
l'idée de Teddy-mension est bien meilleure que la mienne, et semble très utilisable. Par contre, en regardant de plus près, je trouve deux équations équivalentes !!
Sinon, Helium0xFF, je ne comprends pas ta question. J'ai parlé d'équation, donc de droite. Maisest bien un vecteur, et si tu en as besoin ...
Une question : Cet exercice est-il donné seul, ou bien est-ce la deuxième question d'un exercice plus vaste ? Ou la troisième, ...
Cordialement
C'est exercice est donné seul, c'est un DM.
Bonsoir. Avec Xcas voici ce que je trouve:
Soit m la pente de la droite (AC)
m est la solution positive de l'équation:
On a:
Puis:
Ce qui n'incite pas à chercher !
Mais rien pour l'instant ne prouve qu'il n'y a pas une écriture simple de a
C'est sûrement le cas sinon cet exercice n'aurait pas été donné au lycée !
Avec la methode de Teddy j'ai 2 équations :
1+2a+a²=c+c²
1+2a+a²=1+c²+c
Et en effet ce sont les mêmes !
Sur Géogebra j'ai a=1,26 et c'est à peur près la racine cubique de 2.
Donc résolu ?
Non !
Sur Géogebra j'ai juste utilisé la fonction mesure.
Par contre avec les 2 équations je ne peut rien en faire !
Oula, ça voudrait donc dire que 0 = 1 ? :BEnvoyé par helium0xFF
Mais en effet, excusez-moi, j'ai parlé trop vite, ça semblait trop facile.. On a bien 2 équations identiques, qui nous avancent à rien du tout. x)
En développant le calcul perso, j'arrive à cos 120 = -0.5. C'est totalement inutile.
J'ai essayé avec d'autres méthodes, j'arrive toujours soit à 2 équations identiques, soit à 3 équations à 3 inconnues..
Je m'y penche davantage dessus demain !
Confirmé avec le logiciel de calcul formel ! a=2^(1/3)
Il faut donc démontrer que a^3=2 avec vos équations
Désolé j'ai pris mes désirs pour des réalités !
Le test sur Xcas simplifier(a^3-2)==0 renvoie faux
Donc a^3=2 n'est qu'une conjecture presque sûrement vraie
Bonjour,
Sauf erreur, en projetant le point D sur AB on a un point M tel que DM/AD = CB/AC avec DM = 0,5.b AC = a+1 et CB connu, ce qui permet de sortir b et conduit à b² = 3 / (a+1)²
D'autre part dans DCE on a : a² = b²+1
On élimine b² et l'on trouve, après cuisine, une équation du 4ème degré en a, qui se résume au produit (a+2)(a^3-2)=0 d'où a = (2)^(1/3) = 1,2599...(l'autre racine a = -2 n'a pas de signification ici)
Cordialement
Dernière modification par mécano41 ; 27/05/2012 à 11h43.
Comment démontre-t-on cela ?
ça me fait penser à thalès.
Oui, ou bien cela revient à écrire que le sinus de l'angle CAB ou angle DAM est le même dans les deux expressions...
Cordialement
Merci !
Voilà l'équation qui manquait !
Enfermé dans Al-Kashi alors qu'il suffisait de Pythagore et Thalès !
Presque un exercice de collège
Je vais poster sur le forum de Xcas pour signaler le problème de simplification formelle.
Désolé mais j'ai du mal !
Qu'est ce qui permet de dire que DM = 0,5b ?
Apres ça sa va j'ai une équation du 4eme degré.
le triangle DME est la moitié d'un triangle équilatéral comme BCE
Ok
J'arrive à trouver 'a' mais en trichant un peu...
Je n'arrive pas à passer de a^4-2a+2a^3-4 = 0 à (a+2)(a^3-2).
Bonjour
Normal, il y a une erreur. La mise en équation aboutit à la formule (a+1)3(a–1)=3 , soit encore a4+2a3–2a–4=0, dont –2 est réellement une racine évidente.
Je ne vois pas d'erreur ; il a écrit la même chose que toi mais en ordre différent...
Cordialment
Exact. J'avais mal vu l'inversion de l'ordre des puissances.
(NB: le forum propose un mode d'édition avancé qui permet de rendre les textes beaucoup plus lisibles. Je vous incite vivement à vous en servir.)
–2 est une racine évidente, donc on peut mettre le terme (a+2) en facteur, et chercher le polynôme d'ordre 3 qu'il doit multiplier.
et bien merci de votre aide à tous !
Bien vu, Mécano41 !
