Bonjour,
J'aimerais connaître les probabilités pour qu'un événement se produise, mais pour ne pas compliquer trop les choses, je vais simplifier en prenant deux jeux de 64 cartes .
Dans le premier jeu, je sort 16 cartes au hasard.
Dans le second jeu, je sort 16 cartes au hasard.
Question: Combien de chance ai-je d'avoir au moins 8 cartes similaires?
J'ai essayé de calculé sans formule mathématique, puisque je ne les connais pas, et j'arrive à cette réflexion:
pour chaque carte tirée dans le second jeu, j'aurais 16 chances sur 64, soit 1 chance sur 4
Pour que je gagne, je n'ai besoin que de 8 cartes similaires, donc 4 exposant 8 = 65 536
Et comme j'ai le droit de tirer 16 fois, je divise par 16 (mais alors là, pas du tout sûr de moi) = 4096
Ce qui ferait donc 1 chance sur 4096 pour que ça se produit.
Sans doute que ce n'est pas ça? Pouvez-vous m'aider?
Merci
-----




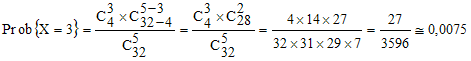
 avec
avec