Probabilités : Tirage successif

[invite0a7791c7]

Bonjour, j'ai un petit problème sur un exercice où il est question de tirage successif sauf que je n'arrive pas à faire mon arbre.
Est ce normal ? Si, non pouvez vous m'expliquer la méthode à appliquer. Merci
-----

[PlaneteF]

Bonsoir, ... et quel est cet exercice ?!

[invite0a7791c7]

En faite une urne contient 10 boules, 5 rouges et 5 noires et au hasard on tire 3 boules successivement.

[invite0a7791c7]

En plus de cela, on a des autres informations à placer comme
_si un joueur obtient 3 boules rouges, événement que l'on appelle A3, il gagne 75 euros.
_S'il obtient 2 boules rouges et 1 verte, évènement que l'on appelle A2, il gagne 45 euros.
_S'il obtient moins de 2 boules rouges évènement que l'on nomme B

[A voir en vidéo sur Futura]

[invite0a7791c7]

B correspond à il ne gagne rien

[PlaneteF]

En faite une urne contient 10 boules, 5 rouges et 5 noires et au hasard on tire 3 boules successivement.

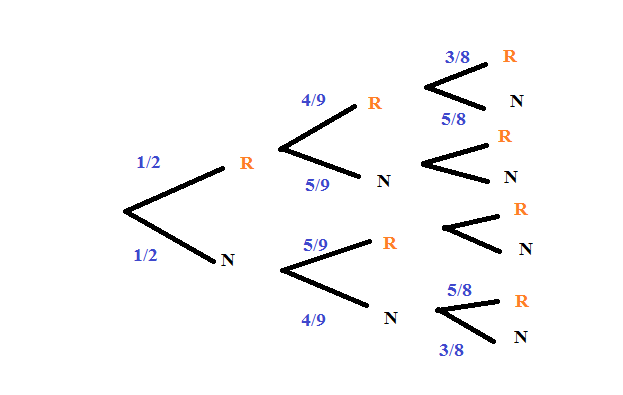
La racine de l'arbre va donner 2 noeuds R (pour rouge) et N pour noir, qui eux mêmes vont donner chacun 2 noeuds supplémentaires R et N (donc 4 nouveaux noeuds au total), qui eux vont donner chacun encore 2 noeuds R et N pour un total de 8 noeuds supplémentaires.

Le poids sur les deux 1^ères branches est de 1/2, ensuite il faut savoir si les boules sont remises ou pas dans l'urne.

[invite0a7791c7]

non, il n'y a pas de remise cela veut dire qu'on les déduit !?

[invite95c5cd5f]

je vais t'aider ooops.
on tire 3 boules c'est des tirages indépendant. alors c'est une loi de bernouli.
il y a card univers=C10 3
apres on tire 3 boules rouges. ça fait C5 3xC5 0/C10 3
apres on tire 2 boules rouges et une verte. ça fait C5 2xC51/C10 3
on tire moins de 2 boules rouges: ça fait C5 0XC5 3/C10 3+C5 1XC5 4/C10 3
j'ai révisé cette loi de bernouli il y a peu utilisateur ooops, vous me direz si cela juste.

[invite95c5cd5f]

je retire ce que j'ai dit car le tirage est sans remise. faites votre arbre.

[PlaneteF]

non, il n'y a pas de remise cela veut dire qu'on les déduit !?

Imagine que tu tires une boule N au 1^er tirage (probabilité=1/2), ... dans ce cas il reste dans l'urne 5 boules R et 4 boules N.

Ainsi, si tu ne remets pas la boule dans l'urne, la probabilité de tirer une boule N au 2^nd tirage est donc de 4/9 (elle aurait été de 1/2 avec remise).

[invite95c5cd5f]

pour l'arbre:
1/2R _ 4/9R _ 3/8R
UNIVERS _5/8N
_ 5/9 N _4/8N
_4/8N
1/2N _ 5/9R _4/8R
_4/8N
_ 4/9N _3/8N
_5/8R

[invite95c5cd5f]

ça a pas pris les espaces. j'ai uploadé votre arbre utilisateur ooops
à cette adresse: http://www.sendspace.com/file/aru8fg

[invite0a7791c7]

Pour l'instant j'obtient sa mais je suis pas sûre

[invite95c5cd5f]

piece jointe pas valide il est dit.
C'est une loi hypergéométrique, je me suis renseigné. PlaneteF confirmera ce que j'ai dit j'espere.

[invite0a7791c7]

Vous avez dit que l'arbre qui correspondait était celui-ci :

Mais j'ai pas compris les probabilités 4/8

[invite95c5cd5f]

ben quand on a tiré 2 boules il en reste 8. alors si on tire une boule de chaque couleur il en reste 4rouges et 4 noires. alors ça fait 4/8 d'en tirer 1 rouge ou une noire. on peut simplifier par 1/2. Le spécialiste planeteF confirmera s'il télécharge mon arbre. Vous pouvez vérifier qu'a chaque branche de l'arbre ça fait 1. si vous etes au collège votre professeur a du vous le dire.

[invite95c5cd5f]

un exemple qu'on prend: on tire que des rouges: ça fait 1/2*4/9*3/8=0,083

[invite0a7791c7]

Si, je sais mais en faite vu qu'il y a 3 tirages successifs donc je dois rajouté des branches, c'est pour cela que je vous ai demander à propos 4/8

[invite95c5cd5f]

y a pas de branche a rajouter. sauf a partir de l'univers, j'ai oublié de les mettre
donc premier tirage 1/2 ça c'est sur. apres il y a les trucs avec les /9 et le troisieme tirage avec les /8. je suis sur de mon coup.

[invite95c5cd5f]

je vous incite à vérifier que les probabilités sont bonnes en utilisant la loi hypergéométrique. la je ne me sens pas de le faire mais je ferai une démonstration demain.

[invite0a7791c7]

Ah d'accord

[invite95c5cd5f]

vous etes en quelle classe? au college ou au lycée? il me parait clair que votre profé veut introduire la loi hypergéométrique avec cette arbre. Autant prendre de l'avance sur le cours.

[invite0a7791c7]

Je suis au lycée

[invite95c5cd5f]

oui je pensais aussi qu'au college on ne voyait pas les probabilités. ça fait bien longtemps que j'ai quitté le college. les programmes ont bien changé depuis. d'ailleurs je ne sais pas si la loi hypergéométrique est au programme. le bac a bien changé.
l'éleve moyen a son bac désormais http://www.routard.com/images_conten...2/pt111443.jpg
Bon au moins vous avez votre exercice de fait la.

[invite0a7791c7]

Non, mon exercice n'est pas finis mais j'essaye de le faire sans aide et si j'ai un problème je demanderai, il y a des question sur des calculs d'évènements, les variables aléatoires, loi de probabilité et d'autres questions avec d'autres paramètres en jeu etc

[invite95c5cd5f]

ben ecris les je fais puis tu viendras verifier

[invite0a7791c7]

Il faut calculer :
_l'évènement A3, soit un tirage de 3 boules rouges, gain = 75 euros.
_l'évènement que l'on appelle A2 soit Si on obtient 2 boules rouges et 1 noire, gain = 45 euros.
_l'évènement que l'on nomme B, soit moins de 2 boules rouges il ne gagne rien
Pour cette question pas de problème
Après on a :
X = la variable aléatoire obtenant le gain du joueur
_il faut donner la loi de proba X + espérance mathématique

Puis en deuxième partie on sait que :
lorsque le joueur réalise l’évènement A3 ou A2, il ne gagne plus l’argent directement mais il est qualifié pour la suite du jeu, donc l’évènement B = pas de qualification au jeu

Le jeu consiste à extraire 1 boule parmi les sept restées dans l’urne : si elle est noire le joueur gagne 150 euros et si elle est rouge il gagne 30 euros :
_Quelle est la proba de gagner les 150 euros sachant que A3 est réalisé ?
_Quelle est la proba de gagner les 150 euros sachant que A2 est réalisé ?
_En déduire la proba de gagner les 150 euros.
_On note W la variable aléatoire donnant le gain du nouveau jeu. W peut prendre les valeurs 0.30 ou 150.
_Calculer la loi de probabilité de W et son espérance afin de comparer avec celle de X.

Voilà

[invite95c5cd5f]

utilisateur ooops:
p(X=75)=1/2*4/9*3/8=12/72=1/6
P(x=45)=3*1/2*4/9*5/8=60/144=5/12
p(x=0)=5/12

[invited3a27037]

bonsoir

va voir cette page de wikipédia
http://fr.wikipedia.org/wiki/Loi_hyp...om%C3%A9trique

en comprenant d'ou sort la formule qui donne P(X=k)

[invite95c5cd5f]

ooops voici la loi
Y suit une loi hypergéométrique de parametre 3, 10, 5 et d'espérance 3*5/10=1,5
P(X=k)=C 5 k * C 5 3-k / C10 3
on vérifie avec P(X=75)=P(Y=3)=1/12.
bon je m'étais trompé dans les calculs dessus c'est celui la qui est bon. utilisateur ooops vous pouvez tout finir.