Problème de suites avec triangle direct 1ère S

[Kiikoo]

Bonsoir, j'ai un petit problème avec un exercice :s je vous avoue que j'ai déjà demandé de l'aide sur un autre forum mais la personne qui m'a "aidé" ne semblait pas patiente et m'a clairement signifié que je comprenais rien à rien et que ma place était à l'école élémentaire. Désolée de ne pas être un génie J'espère trouver de l'aide pour m'aider à comprendre sur ce forum

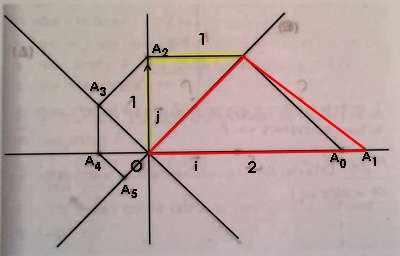
Voici l'énoncé et la figure qui va avec
Soit (O;i;j) un repère orthonormé, (D) : y=x et (delta) : y=-x.
Soit le point A0 (2,0) et A1 le point tel que le triangle OA0A1 soit rectangle isocèle direct en A1.
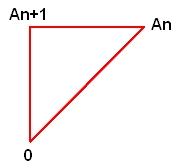
Soit A2 le point tel que le triangle OA1A2 soit rectangle isocèle direct en A2, et de façon général An+1 est le point tel que le triangle OAnOAn+1 soit rectangle isocèle direct en An+1

Sans titre 5.jpg

Mes QUESTIONS/REPONSES :

1°) Calculer OA0 ; OA1 et OA2

OA0 (2,0) OA0 = 2
OA2 (0,1) OA2 = 1

Pour OA1 ( ce que je n'ai pas su faire), la personne m'avait dit que OA0² = OA1² + OA1² = 2 OA1² soit 2² = OA1² + OA1² = 2 OA1²
ce qui me donnait donc ile_TEX.gif donc ile_TEX (1).gif

Je n'ai absolument pas compris la démarche :s Pourquoi avons-nous DEUX fois OA1² + OA1² et pas OA1² + A0A1² ?

2°) Exprimer OAn+1 en fonction de OAn
Pour cette question, elle m'avait écrit OAn² = OAn+1² + An+1An² = 2 OAn+1² ce que je ne comprends pas :/ lorsqu'on écrit OAn+1 en fonction de OAn pourquoi avons-nous des carrés ? je n'ai pas vu ce genre de situation dans les exos du livre donc ça me prend un peu au dépourvu. Ecrire l'expression doit être simple normalement non ?

3°) an = OAn. Déduire la nature de la suite (an)
4°) Déterminez l'expression de an en fonction de n, avec n entier naturel

Pour les questions 3°) et 4°) je ne pense pas pouvoir les faire si je n'ai déjà pas compris les premières ^^

Pourriez-vous m'aider en m'expliquant pour que je comprennes mieux ?
Je vous remercie d'avance
-----

[gerald_83]

Bonsoir

Pourquoi avons-nous DEUX fois OA1² + OA1²

tout simplement parce que le triangle en question est isocèle par définition (Cf l'énoncé)

Est-ce plus clair maintenant avant de passer à la suite ?

[Kiikoo]

Ok donc on est dans le triangle OA0OA1 donc ça formerait ça alors :

[gerald_83]

Re,

J'attends la validation de la pièce jointe mais suis pas sûr de rester connecter encore longtemps

[A voir en vidéo sur Futura]

[Kiikoo]

d'accord pas de problème je comptais me déconnecter mais lorsque j'ai vu que vous m'aviez répondu j'ai répondu en retour ^^

[Kiikoo]

je vais me déconnecter j'espère que l'on pourra reprendre demain !
A bientot

[ansset]

non, depuis le depart , A0 est mal placé ds le graphique mais cela ne change pas grand chose à l'exercice.
ceci dit pour y repondre il faut vraiment connaitre la classe ou tu es.
pour ne pas prendre des solutions non vues en cours..

[Kiikoo]

je suis en 1ère S

[gg0]

En fait, c'est A₁ qui est mal placé. Il est facile de faire la figure à partir des consignes de l'énoncé et de voir que A₁ est un point de la "spirale" qui n'est bizarrement pas nommé.

Cordialement.

[Kiikoo]

La figure de mon prof est fausse ?! :O donc A1 est placé ici alors :


si oui, j'ai juste à appliquer pythagore après donc pour le triangle OA1OA2 pour trouver la longueur OA1

---> Dans le triangle OA1OA2, rectangle en A2, on a :
OA1² = OA2 ² + OA1OA2²
OA1² = 1² + 1²
OA1² = 1 + 1
OA1² = 2
OA1 = racine carrée de 2

[Kiikoo]

Pour la 2°) je pourrais avoir des explications plus précises svp ?

[gg0]

Le triangle OAnA_n+1 est par définition rectangle en A_n+1 et isocèle (" A_n+1 est le point tel que le triangle OA_nA_n+1 soit rectangle isocèle direct en A_n+1") Tu peux donc y faire exactement le même calcul et obtenir OA_n+1 = ... où la seule valeur inconnue après le = est OA_n.

Cordialement.

[Kiikoo]

Le triangle OAnAn+1 est par définition rectangle en An+1 et isocèle (" An+1 est le point tel que le triangle OAnAn+1 soit rectangle isocèle direct en An+1") Tu peux donc y faire exactement le même calcul et obtenir OAn+1 = ... où la seule valeur inconnue après le = est OAn.

Je pourrais donc représenter tout cela par cette figure-ci :

pour obtenir OAn+1 c'est pythagore aussi ça sera donc OAn+1² = AnAn+1² + OAn²

[ansset]

oui en montrant l'angle qui se repète en A(n+1) : (0,A(n+1),An) : (0,(An+2),A(n+1))

[Kiikoo]

comment ca l'angle se repete en An+1 ? Je n'ai pas trop compris :s comment on se retrouve avec An+2 ?

[Kiikoo]

re bonsoir ! j'ai essayé de chercher à comprendre ce que je n'avais pas compris dans mon message précédent mais sans succès :S je ne vois pas comment l'angle se répète en An+1 et encore moins comment on obtient le An+2 ...

[gg0]

Fais un dessin du triangle, applique le théorème de Pythagore (en première S, on connaît depuis 2 ans, donc tu peux savoir faire) plus le fait que le triangle est isocèle et conclus.
Tu es en train d'attendre qu'on écrive ce que tu peux écrire seul si tu décides de le faire. Arrête de faire l'âne pour avoir du foin ! Ne te comporte pas plus bêtement que tu n'es.

NB : Il est souvent plus facile de comprendre la situation donnée dans l'énoncé que les explications des autres.

[Kiikoo]

Bon et bien je me lance j'avais fait cela hier mais comme je n'étais pas sur du tout je ne voulais pas poster ...

Je reprends donc tout depuis le début :


1°) Calculer ; et

--> donc

--> D'après le triangle , rectangle isocèle direct en , on a :








--> donc


2°) Exprimer en fonction de
Pour exprimer en fonction de , on utilise le théorème de pythagore.
D'après le triangle , rectangle isocèle en , on a :






Est-ce correct ?

[gg0]

Bonjour.

"...j'avais fait cela hier mais comme je n'étais pas sur du tout je ne voulais pas poster" ??
Si tu ne dis pas ce que tu as fait, comment peut-on savoir ? Tu ne vas pas rendre ton devoir de peur qu'il soit faux ??

Sinon, ce que tu as fait (le 2, je ne reprends pas le début, tu as eu le temps de savoir si c'était juste ou pas) est correct à une erreur de rédaction près :
est faux. Ce qui est correct, c'est
Il faut une accolade autour du n+1 en indice : OA_n^2=2OA_{n+1}^2

Bon travail (n'attends pas qu'on te dise "c'est bon", tu as un cerveau en bon état, toi aussi, tu peux décider si tu appliques les règles des maths ou pas) !

[Kiikoo]

ben je l'aurais rendu mais sans être sure c'est tout ...
Oui j'ai fait une erreur de rédaction :s

merci pour la correction