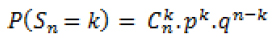[Statistique] Probabilité et loi normale

[invited4ea61e7]

Bonjour,
je suis en train de faire un devoir de probabilité, mais je bute sur la dernière question,
Alors dans l'énoncé il s'agit d'une distribution du poids d'adultes dans la population, celle-ci suit une loi normale d'espérance 73kg et d'écart type 4kg. (c'est un pays fictif hein bon)
Par la suite du devoir il fallait établir le poids minimum à partir duquel on peu considérer un personne "très grosse", celle-ci étant considérée comme telle si elle fait partie des 10% des plus grosses.
j'ai défini ce poids comme ceci :
Soit X le poids de la population modélisée par L(X) = N(73 ; 4).Il faut trouver le poids z tel que 10% des personnes se situent au dessus de ce poids.
1 - P(X > z) = 0,1
On donc P(X > z) = 0,9 = P[ X > (z - µ)/σ ]
Alors (z - µ)/σ est la valeur de la fonction au point 0,9 qui correspond à F(1,2816) = 0,90
Ainsi (z - µ)/σ = 1,2816 ; avec µ = 73 et σ = 4 on a :
Z = (1,2816* σ) + µ = (1,2816*4) + 73 = 5,13 + 73 = 78,13.
Donc dans ce pays fictif, une personne sera considérée "très grosse" car dans les 10% les plus grosses à partir de 78,13kg

Ensuite une enquête a été menée sur 160 personnes, pour savoir si ils se considéraient très gros, et au total 23 d'entre eux ont répondus se considérer très gros. Quelle était la probabilité de tomber sur un tel échantillon si seulement les personnes étant considérées comme "très grosses" avaient répondu se sentir "très grosses" ?

Et là je ne m'en sors pas, je pensais que je pouvais utiliser les factoriels P(S160 k=23)= C (k 160) * p^k*q^(160-k)
avec p = 0,1 et q = 1-p=0,9 et k = 23
Seulement ça m'a l'air tout faux, auriez vous une idée pour m'aider?
Merci beaucoup
-----

[gg0]

Bonjour.

On peut considérer que la population est très grande. Alors, le nombre de personnes très grosses dans un échantillon de taille n suit une loi binomiale (*).

Cordialement.

(*) approximation de la loi véritable, qui est la loi hypergéométrique.

[invited4ea61e7]

Merci pour votre indication, donc la loi binominale que je comptais formuler se présente comme ceci (avec p = 0,1 et q = 1-p=0,9 et k = 23 ) :
L(S160) = B(160 ; 0,1)
La probabilité que je cherche s'écrira :

Mais comment faire ce calcul avec un 'n' si grand? ma calculette ne me permet pas de faire {(160!) / [23!( 160-23)!} * (0.1^23) * (0,9^137)
Les factoriels sont trop grand, donc j'ai du faire à la place de {(160!) / [23!( 160-23)!} : (169*159*158*...*138) / 23!
Et au final je trouve 0,01959
Il n'y aurait que 1,9% de chance de trouver un tel tirage dans cet échantillon?
La probabilité me semble petite non? la démarche et le calcul sont-ils bon?
Merci pour votre aide

[gg0]

La moyenne attendue est 16, l'écart type de l'ordre de 4, on est donc assez loin de la moyenne, à 23. Il n'est pas étonnant que la probabilité soit faible. Je trouve comme toi environ 0,0196. Et de l'ordre de 0,1 pour 16 qui est la valeur la plus probable.
Pour le calcul, connais-tu l'approximation par une loi Normale ?

Cordialement.

[A voir en vidéo sur Futura]

[invited4ea61e7]

Approximation par une loi normale, mhhh, je ne suis pas sûr de comprendre ce qu'il faut entendre par là. Par la loi normale je pense que je ne pourrai que calculer l'intervalle de confiance autour de k/n et non pas la probabilité exacte que k = 23 se produise dans l'échantillon.

[gg0]

Tu as en grande partie raison, car 23 est déjà loin de la moyenne. donc l'approximation devient nettement moins bonne. On le fait par "correction de continuité", c'est à dire qu'on calcule la probabilité d'être entre 22,5 et 23,5. Mais un calcul direct est bien préférable, et les tableurs savent faire. Mon tableur (Calc de Open office - gratuit) donne directement 0,0195928466

Cordialement.