Résoudre des inéquations

[estelledu31]

Bonjour, voila j'ai un dm pour la rentrée, j'ai fais le premier exercice, je pense que c'est bon mais pour le deuxième je ne suis pas trop sure. Donc j'aimerais que vous m'aidiez pour savoir si j'ai juste. Merci d'avance.

Voila l'exercice :
Résoudre chaque inéquation.
a) 3x (x+3)-(x+3)² ≤ 0
b) x³+2x²+x ≥ 0

Pour le a : j'ai mis (x+3) en facteur ça donne : (x+3)(2x+3) et après j'ai fait un tableau de signe (voir image). x+3=0 et 2x+3=0
<=> x=-3 <=>x=-3/2
Pour le b (la je suis vraiment pas sure) : j'ai mis x en facteur ça donne : x(x²+2x+1) et après j'ai fait un tableau de signe (voir image). x=0 et x²+2x+1 est toujours positif sauf si x=0 car le carré d'un nombre est toujours positif (je crois que c'est n importe quoi)

Pour le a : S=[-3;-3/2]
Pour le b : S=[0;+∞[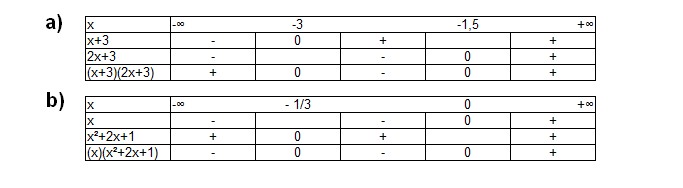
-----

[danyvio]

Pour le b (la je suis vraiment pas sure) : j'ai mis x en facteur ça donne : x(x²+2x+1) et après j'ai fait un tableau de signe (voir image). x=0 et x²+2x+1 est toujours positif sauf si x=0 car le carré d'un nombre est toujours positif (je crois que c'est n importe quoi)

Pièce jointe 212347

x²+2x+1=(x+1)² est toujours > 0 SAUF pour x=-1 (alors l'expression = 0)

[estelledu31]

ah oui c'est une identité remarquable, merci donc après il faut que je remplace dans le tableau -1/3 par -1 et x²+2x+1 par (x+1)² c'est ca ? Et le a est juste ? Encore merci de m'aider

[The_Anonymous]

Le a) est tout à fait juste

Pour le b), oui tu peux faire ces changements en sachant que

[A voir en vidéo sur Futura]

[estelledu31]

Merci beaucoup

[The_Anonymous]

Tes tableaux sont parfaits, reste plus qu'à ajouter -1 à ta réponse initiale

Cordialement

[PlaneteF]

Bonsoir,

a) 3x (x+3)-(x+3)² ≤ 0

(...)

Pour le a : j'ai mis (x+3) en facteur ça donne : (x+3)(2x+3)

Non c'est faux, il y a une erreur de signe !

Pour le a : S=[-3;-3/2]

Du coup l'ensemble des solutions pour le n'est pas correct ...

D'ailleurs on voit bien que est une solution de l'inéquation et pourtant il ne fait pas partie de ton ensemble , donc il y a bien un problème !

[estelledu31]

Ah oui merci PlaneteF, je n'avais pas vu mon erreur j'ai oublié de changer le signe en enlevant la parenthèse. Donc ça donne (x+3)(3x-(x+3))= (x+3)(2x-3)
Après je change le tableau de signe (voir image) avec x+3=0 <=> x=-3 et 2x-3=0 <=>x=3/2. S=[-3;3/2]

[The_Anonymous]

Désolé de ne pas avoir vu l'erreur! Et merci PlaneteF =) Et si je ne me tromps pas encore, [-3;3/2] est juste

[estelledu31]

Merci beaucoup a vous deux

[The_Anonymous]

Mais de rien, tout le plaisir est pour (PlaneteF =) ) et pour moi