geometrie Dans l'espace sans coordonée

[invitec911ae32]

Bonjour,
je bloque complétement sur un dm Sur la géométrie dans l'espace ( Pourtant Très Facile à ce qu'on m'a dit ) je ne comprend pas très biens le sens des question

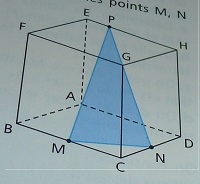
On considère le cube ABCDEFGH et les points M, N et P définis par :

M milieu de [BC] vecteur CN = 2/3 (vecteur)CD EP(vecteur) = 1/4 EH(vecteur)

Partie A

a. Justifier que les droites (MN) et (AD) sont sécantes en un point appelé L.

b. Préciser la position du point L sur la droite (AD)

c. Déterminer l'intersection des plans (MNP) et (ADE)

d. Déterminer, et justifier la position relative, de l'intersection (d) des plans (MNP) et (EFG).

e. Les points M, N, D, H et F sont-ils coplanaires ?

f. Sur la figure ci contre, tracer la section du plan (MNP) sur le cube.

la figure concerné :




pour la question a ) j'ai dit que les 2 droite sont coplanaire et non parallèle Donc elles sont secantes

pour la question b ) j'ai mal comprit la question mais je les tout de même essayé avec les vecteurs je ne sais pas si c'est la bonne méthode je trouve : AL(vecteur) = 13/10 (vecteur)AD

Pour la question C) je ne sais pas comment .... dois je passer par les droite ( MP) et (NP) Sécantes à ( EH ) ?

j'ai vraiment du mal avec la géométrie spatiale :s donc si quelqu’un peut m'aider s'il vous plait ...

Merci d'avance pour votre aide
-----

[invite427a7819]

Bonsoir,

Pour ce qui est de la question b, ce que vous proposez est une réponse acceptable (dans la forme du moins, je n'ai pas fait les calculs donc je ne connais pas le résultat).

Pour ce qui est de la C, de manière générale quand on cherche l'intersection de deux plans on peut avoir ou bien le vide (si les plans sont parallèles) ou bien tout un plan (si les plans sont égaux) ou bien une droite. Il doit être assez facile de prouver que les plans ne sont ni parallèles ni égaux : on cherche alors à trouver une droite incluse dans les deux plans considérés, donc dans leur intersection : comme il n'y a qu'une droite d'intersection, bim, c'est elle.

Pour cela il suffit de vérifier que deux points (bien choisis) ont une bonne raison de se trouver sur les deux plans (si deux points appartiennent à un plan, la droite passant par ces points y est incluse). Au vu des premières questions, je dirais que L est sans doute l'un de ces points...

Dans ce genre de cas, un dessin précis peut être un véritable atout. En avez-vous fait un ?

[invitec911ae32]

Bonsoir Elwyr,

Dans ce genre de cas, un dessin précis peut être un véritable atout. En avez-vous fait un ?

J'en ai fait un de profil selon le plan (GCD)

les point L et P appartiennent au 2 plan MNP ET (ADE) ( en " étalant " les plans )

le Plan (MNP) coupe le plan (ADE) selon une droite (PL)

les plans (MNP) et (ADE) ne sont pas parallèle car 2 droite sécantes (PM) et (PN) du plan ( MNP) ne sont pas parallèle au plan (ADE) $

cela suffit pour dire qu'elle sont sécantes ?

[invite427a7819]

J'en ai fait un de profil selon le plan (GCD)

Je pensais plutôt à un dessin dans l'espace.

les point L et P appartiennent au 2 plan MNP ET (ADE) ( en " étalant " les plans )

Je ne sais pas ce que vous entendez par "étaler les plans", mais tant que ça marche... En général, les arguments qu'on utilise sont du type "les droites D₁ et D₂ sont incluses, respectivement, dans les plans P₁ et P₂ et sécante en S, donc S appartient à P₁ et P₂"

les plans (MNP) et (ADE) ne sont pas parallèle car 2 droite sécantes (PM) et (PN) du plan ( MNP) ne sont pas parallèle au plan (ADE) $

cela suffit pour dire qu'elle sont sécantes ?

Cela suffit, mais n'est à mon avis même pas nécessaire. Deux plans parallèles qui ont un point commun sont égaux, sachant que L appartient à (MNP) et (ADE), il vous suffit de trouver un point qui soit dans un plan mais pas dans l'autre... A, par exemple. Enfin, tant que ce que vous avez marche, ça marche.

Votre conclusion me semble juste.

[A voir en vidéo sur Futura]

[invitec911ae32]

Pour la question d) on a Les droites (EH) et (PL) sont sécante et respectivement contenue dans les plans respectifs (EFG) et (MNP) donc les 2 plans sont sécants ?

[invite427a7819]

Cela suffit à dire qu'ils sont sécants ou confondus, mais il est assez clair qu'ils ne sont pas confondus.

Après, je ne pourrai pas vous aider plus, je ne pense, je ne comprends pas vraiment la question non plus.

[invitec911ae32]

Après, je ne pourrai pas vous aider plus, je ne pense, je ne comprends pas vraiment la question non plus.

je pense qu'il demande de montrer que les 2 plans sont sécants et d'en déterminer l'intersections qui est la droite d

mais à part ce que j'ai dit avant je vois pas plus ..

[invitec911ae32]

l'intersection (d) est une droite appartenant à (EFG) et passant par le point P je pense

[invite427a7819]

Y a de bonnes chances. Sachant que (MN) est parallèle à (EFG), je pense même que vous pouvez la caractériser complètement.

[invitec911ae32]

Merci Pour votre Aide Elwyr sans vous je n'aurais pas pu faire ce Devoir maison

Bonne soiré/ nuit