Comprendre et appliquer méthode des moindres carrés

[mlleceliine]

Bonjour,
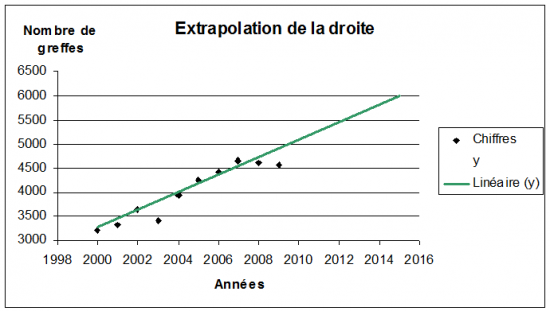
Je suis en 1ère S et je réalise un TPE sur les cellules souches qui réunit 2 matières : la SVT et les maths. Mais voilà : pour introduire un peu de mathématiques dans notre tpe, nous avions décidé, (avec mon groupe), de réaliser un graphique sur le nombre de greffes de cellules souches dans les années à venir grâce à une extrapolation de droite. Cette idée m'est en fait venue d'un blog qui lui même faisait un TPE sur les cellules souches et qui avait donc déjà réalisé ce graphique que voici :

Avec l'explication + bas : "Nous avons utilisé la technique de l’extrapolation afin d’obtenir des prévisions concises des années futures.
Nous avons commencé par calculer la somme des résidus afin de tracer la droite des moindres carrés. Nous avons ensuite déterminé le coefficient directeur de la droite : y= 181.24x-359200 par l’usage de la calculatrice. Ensuite, on a remplacé x par les années correspondantes afin de tracer la droite de régression."

Maintenant, ce que j'aimerais savoir c'est si cette droite est correctement construite et surtout avoir une réelle explication de ce QU'EST cette méthode des moindres carrés (car la brève explication du dessus ne me paraît pas très claire...:S). Bien sûr, si le graphique comporte des erreurs, nous referons toute la manip', ça va de soi, mais il faudrait avant tout que l'on sache comment procéder...En espérant avoir une réponse au plus vite, merci d'avance

Céline
-----

[Paraboloide_Hyperbolique]

Bonjour,

Le document suivant donne les formules: http://math.unice.fr/~diener/MAB07/MCO.pdf

Si vous souhaitez plus d'explications, n'hésitez pas à le demander.

[gg0]

Bonjour.

Sans les valeurs exactes, il est généralement impossible de savoir si la droite est la bonne. Mais ici il est évident que la droite tracée n'est pas correcte (les points au dessus de la droite en sont très proches, ceux qui sont au dessous s'en éloignent souvent et bien plus. Or comme on prend les carrés des distances ...
Si vous avez les valeurs, une calculette statistique permet d'obtenir les coefficients, ou un tableur (ORDONNEE.ORIGINE et PENTE).

Cordialement.

[mlleceliine]

Bonsoir,
Après maintes et maintes recherches, je suis finalement arrivée à trouver une "espèce" d'équation de la forme y=169x+3002 en calculant a par la formule a=somme des (xi−xbarre)(yi−ybarre)/somme des (xi-xbarre)² (en gros celle notée sur le document pdf mais en détaillée et b en remplaçant ybarre, a et xbarre dans l'équation ybarre=abarre*x+b
J'ai pris pour cela des données approximatives, correspondant aux années 2000 jusqu'à 2004, ce qui explique sûrement l'énoorme écart entre mes valeurs calculées pour les années suivantes et celles affichées sur le graphique (par les points). Par exemple : pour prévoir le nombre de greffes qu'il y aura en 2005, je fais y=169*5+3002=3847 =>>Et sur le graphique (supposée donc être la "vraie" valeur), je retrouve à peu près 4250...!:O
Je pense que mes valeurs inexactes y jouent pour beaucoup dans l'histoire, mais le problème c'est que je n'ai pas les données de départ. ça fait déjà plusieurs semaines que l'on cherche des chiffres quant aux greffes de cellules souches et, hormis ce graphique, rien à l'horizon pour l'instant...(d'ailleurs, si vous avez qqc, je suis prenante )

[A voir en vidéo sur Futura]

[Dlzlogic]

Bonsoir,
L'ajustement linéaire est une opération assez simple lorsqu'on applique les formules (cf. la doc de Paraboloide-hyperbolique).
Si j'avais le courage, d'après le graphique que vous affichez, il n'est pas difficile de lire les couples de valeur (x,y).
Je pense que vous devriez d'abord comprendre le principe de la méthode, et ensuite l'appliquer.
Bien-sûr le problème sous l'aspect médical est insaisissable pour moi, par contre le calcul que vous évoquez est simple.
Donc, un conseil, listez les couples de valeurs (nombre de greffe - années) que vous possédez et dites nous ce que vous avez fait.

[gg0]

Bonjour

Et sur le graphique (supposée donc être la "vraie" valeur), je retrouve à peu près 4250...!

C'est normal, tu traces une droite correspondant aux points du début, qui sont "plutôt bas. Tu peux essayer avec des valeurs approchées de tous les points du graphique. par contre, le modèle que tu obtiendras ne correspondra pas aux valeurs utilisées (sauf cas particulier) car il s'agit de trouver une droite qui passe "au plus près" des points, puisqu'elle ne peut pas passer par les points, ils ne sont pas alignés.

Cordialement.

[Paraboloide_Hyperbolique]

Bonsoir,
Après maintes et maintes recherches, je suis finalement arrivée à trouver une "espèce" d'équation de la forme y=169x+3002 en calculant a par la formule a=somme des (xi−xbarre)(yi−ybarre)/somme des (xi-xbarre)² (en gros celle notée sur le document pdf mais en détaillée et b en remplaçant ybarre, a et xbarre dans l'équation ybarre=abarre*x+b
J'ai pris pour cela des données approximatives, correspondant aux années 2000 jusqu'à 2004, ce qui explique sûrement l'énoorme écart entre mes valeurs calculées pour les années suivantes et celles affichées sur le graphique (par les points). Par exemple : pour prévoir le nombre de greffes qu'il y aura en 2005, je fais y=169*5+3002=3847 =>>Et sur le graphique (supposée donc être la "vraie" valeur), je retrouve à peu près 4250...!:O
Je pense que mes valeurs inexactes y jouent pour beaucoup dans l'histoire, mais le problème c'est que je n'ai pas les données de départ. ça fait déjà plusieurs semaines que l'on cherche des chiffres quant aux greffes de cellules souches et, hormis ce graphique, rien à l'horizon pour l'instant...(d'ailleurs, si vous avez qqc, je suis prenante )

Bonsoir,

Vous n'obtiendrez jamais de vraies valeurs. Cette méthode est approximative. Rien ne dit que la relation entre les axes x et y du graphe est linéaire (c'est une hypothèse qui est faite par le modèle). De plus, moins vous prenez de points en compte, moins il sera possible d'inférer une conclusion correcte à partir du modèle linéaire.

Concernant l'obtention approximative des coordonnées à partir d'un graphe sous forme d'image, vous pouvez vous servir du logiciel "g3data". http://www.frantz.fi/software/g3data.php --> version windows en bas de page "g3data 1.4.0rc4 Windows XP executable zipped,"

[Tryss]

Concernant l'obtention approximative des coordonnées à partir d'un graphe sous forme d'image, vous pouvez vous servir du logiciel "g3data". http://www.frantz.fi/software/g3data.php --> version windows en bas de page "g3data 1.4.0rc4 Windows XP executable zipped,"

Sinon, Libre office (et probablement Excel) sait faire la méthode des moindres carrés :
https://help.libreoffice.org/Calc/Ar...s/fr#DROITEREG

[Dlzlogic]

Bonsoir,
En fait j'ai pas compris si notre amie cherche à comprendre la méthode des moindres carrés, à apprendre à résoudre un type de problème ou à résoudre un cas particulier, en l'occurrence celui qui est présenté dans le premier message.
Je remarquerai tout de même que l'ajustement par une droite est un cas particulier de la méthode.
La compréhension de la méthode permet des possibilité intéressantes.

[mlleceliine]

Bonsoir,

Dlzlogic
Re : Comprendre et appliquer méthode des moindres carrés

Bonsoir,
En fait j'ai pas compris si notre amie cherche à comprendre la méthode des moindres carrés, à apprendre à résoudre un type de problème ou à résoudre un cas particulier, en l'occurrence celui qui est présenté dans le premier message.
Je remarquerai tout de même que l'ajustement par une droite est un cas particulier de la méthode.
La compréhension de la méthode permet des possibilité intéressantes.

Eh bien en fait j'aimerais, comme vous dîtes, appliquer cette méthode à un cas particulier mais aussi être capable de l'expliquer lors de notre oral donc pour cela, il faut que j'en connaisse le principe (qui ne semble pas bien compliqué pr vous mais dont les formules restent plutôt floues pour moi :S). J'ai téléchargé le logiciel afin de retrouver les données de manière plus exacte, mais je m'occuperais de ça dès demain et vs communiquerez mes "calculs" effectués !
Quant à votre dernière phrase, je suis certaine que cette méthode offre beaucoup plus de possibilités que celle de l'extrapolation de droite recherchée ici (qui peut peut-être sembler minime à côté) mais voilà, le fait est que je n'ai plus tellement de temps et que, bien sûr, j'aurais pu approfondir cette méthode, peut être pas en comprendre l'intégralité mais au moins découvrir ce que tout ce qu'elle proposait, mais je pense aussi qu'avec le peu de temps qu'il nous reste, il faut aller droit au but et ne pas tenter 36 chemins (à approfondir peut-être plus tard, qui sait ;])

[gg0]

Bonjour.

Le principe de la méthode :
On cherche un droite passant "au plus près des points". En notant M_i(x_i,y_i) les n points du nuage, on cherche une équation y=ax+b de façon que les points soient "au plus près de la droite". Il y a différentes façons de voir ce que signifie ce "au plus près".
Une autre façon de voir est de dire : on veut un modèle affine y=ax+b des relations entre les x_i et les y_i, donc une relation y_i=ax_i+b+e_i où e_i est une petite erreur (due à des imprécisions, des erreurs de mesure ou une variabilité naturelle).
Historiquement, pour diverses raisons, on s'est arrêté à l'idée : La somme des carrés des e_i doit être la plus petite possible (la moindre). De cette façon, on passera au coeur du nuage de points. Et les "distances verticales" entre les points et la droite seront faibles, car y_i-(ax_i+b)=e_i est justement, au signe près la distance verticale (voir sur un dessin).
Cette condition "somme des (e_i)² minimale donne dans un premier temps que la moyenne des e_i doit être nulle :

ce qui se traduit par le fait agréable que la droite passe par le point moyen du nuage, son centre de gravité, et donne pour b :

En remplaçant dans les e_i :
doit être minimal.
On trouve le minimum de cette fonction en cherchant où sa dérivée s'annule. Je ne fais pas le calcul, mais il donne l'autre formule.
Tu retrouveras ce genre d'explication dans certains cours sur l'ajustement linéaire.

Cordialement.

[Dlzlogic]

Bonjour,
En complément, voici les résultats de l'extrapolation linéaire

Pour des raisons de précision (appelées aussi erreur d'arrondi) l'année de départ est l'année 100.
C'est à dire qu'on retire 1900 à toutes les dates
Régression linéaire Y=A + B * X nbpts=10 A = -16887. B = 199. R2 = 0.883 (emq=219.841)

X=2010.00 ==> Y=5047
X=2011.00 ==> Y=5246
X=2012.00 ==> Y=5446
X=2013.00 ==> Y=5645
X=2014.00 ==> Y=5844
X=2015.00 ==> Y=6044
X=2016.00 ==> Y=6243

On remarque que le coefficient d'indétermination R2 n'est pas très bon, ce qu'on savait déjà au vu de la courbe.
L'emq (écart-type) est 220.

Détail du calcul.
La somme des carrés des écarts à la moyenne est la variance. La meilleure précision du résultat sera obtenue pour une variance minimale, d'où l'appellation "méthode des moindres carrés".
L'équation de la droite cherchée est y = a + bx.
Les termes a et b sont les solutions du système linéaire suivant :
an + bS(X) = S(Y)
aS(X) + bS(X²) = S(XY)
où S() est la somme, notée généralement sigma majuscule, n le nombre de couples (X,Y).

Si vous voulez utiliser cette méthode, je vous conseille vivement de faire le calcul détaillé, vous-même, au moins une fois.

[leon1789]

La somme des carrés des écarts à la moyenne est la variance.

Non, la variance est la moyenne des carrés des écarts à la moyenne d'une série z_i :