Logique simple

[MAROMED]

Est ce que la 2 eme démonstration est vraie ??
merci par avance
Cordialement.
-----

[Médiat]

Bonsoir,

Vous pourriez nous dire ce que vous avez déjà fait au lieu de nous demander de faire vos exercices !

[MAROMED]

Bonsoir,

Vous pourriez nous dire ce que vous avez déjà fait au lieu de nous demander de faire vos exercices !

je ne demande pas a vous de faire mes exercices. l’exercice tu le vois bien est faite par deux méthodes la premier est tiré du livre est la deuxième j'ai le fait moi même. et je suis ici pour nous discutons les deux méthodes. n y a rien faire Médiat.

[invite2c46a2cb]

Bonsoir,
Je pense que ce que Médiat voulait dire était la chose suivante : Qu'en pensez-vous, personnellement ? Vous la trouvez fausse ? Y a-t-il un passage qui n'est pas clair et qui vous fait douter de sa véracité ?

[A voir en vidéo sur Futura]

[eudea-panjclinne]

C'est la classique démonstration à l'envers, elle part d'une proposition à démontrer dont on ne sait pas si elle est vraie ou fausse.
Voici un exemple de ce type de raisonnement faux:
je veux démontrer que 1=2.
Je pose 1=2.
je multiplie les deux membres par 0, c'est "possible".
Je trouve 0=0.
C'est vrai dont ce qui est posé au début est vrai.
Ce raisonnement serait vrai si les différentes lignes posées étaient équivalentes mais ce n'est pas le cas !


Pour que la démonstration proposée par Maromed soit correcte il faut l'écrire à l'envers (commencer par la fin), ce qui est faisable puisque toutes les lignes sont équivalentes.

[MAROMED]

d’accord Teddy-mension je comprend et merci eudea-panjclinne mais il me semble que c'est le même idée d'un autre exemple

[topmath]

Bonsoir tout le monde

Pour que la démonstration proposée par Maromed soit correcte il faut l'écrire à l'envers (commencer par la fin), ce qui est faisable puisque toutes les lignes sont équivalentes.

Si votre proposition est juste on remarque , que dans la réponse de MAROMED tout les lignes utilisant des implications et non des équivalences dument ce que je constate sur ça réponse .

Cordialement

[PlaneteF]

d’accord Teddy-mension je comprend et merci eudea-panjclinne mais il me semble que c'est le même idée d'un autre exemple
Pièce jointe 226474

Il n'y a pas de "il faut commencer par ...", ... tu peux montrer au choix A=B ou B=A (réflexivité), donc tu peux bien commencer par ce que tu veux !

[PlaneteF]

tu peux montrer au choix A=B ou B=A (réflexivité)

Oups, lapsus --> "Symétrie"

[eudea-panjclinne]

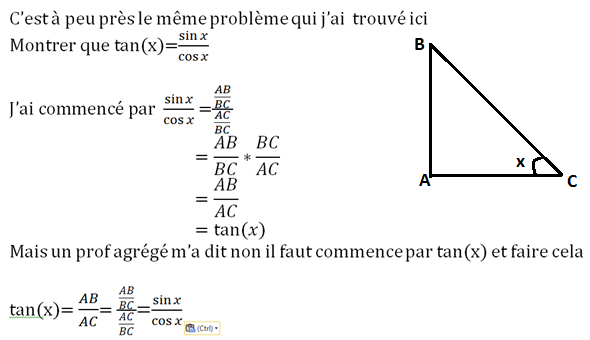
Maromed, lorsque tu as commencé ta démonstration par

le professeur t'a -t-il donné une raison pour laquelle ce n'était pas correcte ?
Personnellement je ne vois pas où est le problème sinon d'éviter de prendre x=90°, de toute façon ce n'est pas un cas de démonstration à l'envers.

Si votre proposition est juste on remarque , que dans la réponse de MAROMED tout les lignes utilisant des implications et non des équivalences dument ce que je constate sur ça réponse .

Désolé, je comprends mal votre question.
Disons que dans la démonstration proposée il n'y a que des implications (symbole =>) c'est ce qui fait que le raisonnement écrit est faux.
Si l'élève avait écrit des équivalences (<=>) il serait ici juste.

Il n'y a pas de "il faut commencer par ...", ... tu peux montrer au choix A=B ou B=A (réflexivité), donc tu peux bien commencer par ce que tu veux !

Pas du tout, une démonstration mathématique ce n'est pas que des calculs, c'est aussi des phrases et des symboles pour lier correctement les affirmations faites et les justifier dans un ordre bien déterminé.
Exemple :
Soient a et b des réels
écrire
a=b
a^2=b^2
est exact, c'est une simple implication (=>) qui fait passer de la 1e ligne à la seconde.
En revanche, il est faux d'écrire :
a^2=b^2
a=b
prendre a=1 et b=-1.

D'une façon générale, quand on écrit, comme ici, des affirmations successives, elles sont déduite les une des autres par des déductions (symbole =>). Chaque ligne impliquant la suivante. Or l'implication n'est pas symétrique : A=> B ne donne pas B =>A. D'où l'importance de l'ordre dans lequel on fait le raisonnement. On pourrait bien sur remplacer les => par des équivalences <=>, mais ce n'est pas toujours possible.

[PlaneteF]

Pas du tout, une démonstration mathématique ce n'est pas que des calculs, c'est aussi des phrases et des symboles pour lier correctement les affirmations faites et les justifier dans un ordre bien déterminé.

On ne parle pas du tout de la même chose, tu as mal interprété mon message (peut-être n'étais-je pas clair).

Je me réferrais au message#6 de MAROMED, qui fait un raisonnement du type : a=b=c=d=e

Donc à partir de là on peut bien évidemment en conclure que a=e (par transitivité) et donc e=a (par symétrie).

... c'est dans ce sens là où je voulais dire qu'il peut commencer par où il veut !

Conclusion : Son premier calcul est correct, et je ne comprends pas trop l'objection qu'il lui a été faite à ce sujet (peut-être a-t-il mal interprété ce qu'il lui avait été dit).

[eudea-panjclinne]

On ne parle pas du tout de la même chose, tu as mal interprété mon message

Au temps pour moi, désolé !

[PlaneteF]

Au temps pour moi, désolé !

Comme l'on dit dans les jeux en ligne : np