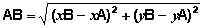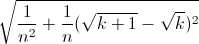L'arc de parabole ! (exercice 1èreS)

[Diamonds]

!
Bonjour !
Je suis confronté à un exercice, et je ne comprends pas un mot... Nous venons d'entamer le chapitre et j'ai du mal à cerner tous ces calculs avec les sigma... Si quelqu'un pourrait m'aider avec le plus de détails et de précisitions possibles, ça serait vraiment génial.
Voici l'exercice

Dans un repère orthonormé (O;I;J) du plan, on appelle C l'arc de parabole représentant la fonction racine carrée sur [0;1], définie par g(x) = CodeCogsEqn.gif

On se propose de calculer une valeur approchée de la longueur L de la courbe C.,
On place sur la courbe les n+1 points A₀ , A₁ , A₂ , ..., A_k , ... A_n, d'abscisses respectives :
0, 1/n, 2/n,... , k/n, 1.
La longueur de la ligne polygonale A₀A₁A₂...A_k...A_n fournit une approximation de la longueur cherchée.

1)
a) Faire une figure dans le cas n=2 fait
b) Donner la valeur exacte de A₀A₁, A₁A2₂, et L. bloqué

2)
Montrer que la longueur du segment A_kA_k+1 est égale à :
CodeCogsEqn(1).gif sacrément bloqué

En déduire que L = CodeCogsEqn(2).gif sacrément bloqué

Ensuite il y a le 3) et le 4), mais je pense que si je comprends déjà les 3 parties où je suis bloqué, je pourrai éventuellement résoudre la suite.

C'est la première fois que je crée un topic, j'espère que vous aurez compris que je n'ai presqu'aucun point de repère sur ce chapitre... Merci beaucoup !
-----

[Teddy-mension]

Bonjour !
Exercice intéressant !

b) Donner la valeur exacte de A₀A₁, A₁A2₂, et L.

D'accord.. Bon, que représente la longueur A₀A₁ ? Et A₁A2₂ ? (exprimées à l'aide de tes différentes coordonnées)
Enfin, tu sais que L est la valeur approchée de la longueur de la courbe.
Donc ici, on a L = ... + ... *complète*

(Pour la suite on verra après..)

[Diamonds]

L = a0a1 + a1a2 !

[Duke Alchemist]

Bonjour.

Ne vois-tu pas des triangles rectangle dont tu dois déterminer l'hypoténuse, non ?

Duke.

[A voir en vidéo sur Futura]

[Diamonds]

Oui...
Donc A0A1 serait calculé de la façon suivante ? A0A1^2 = 1 + (1/2)^2
D'où A0A1 = V(5/4)


V = racine carré

[Teddy-mension]

L = a0a1 + a1a2 !

D'accord !

Donc A0A1 serait calculé de la façon suivante ? A0A1^2 = 1 + (1/2)^2
D'où A0A1 = V(5/4)

Ah non, pas d'accord là.. Regarde bien sur ton schéma. Je rappelle que et ..

[Diamonds]

Ah oui d'accord, alors :

avec la formule suivante

je trouve A0A1 = V(0,75)
est-ce juste ?

[Duke Alchemist]

Re-

Je suis d'accord avec le résultat si ce n'est que je te propose de garder la forme fractionnaire simplifiée mais pas la forme décimale...
Ce n'est que mon avis, tu en fais ce que tu veux

Duke.

[Diamonds]

D'accord ! Pour A1A2 aussi je trouve le même résultat, et comme cité avant, L = A0A1 + A1A2 , d'où L = 2V(3/4) ! (environ égale à 1,73 mais ils demandent la valeur exacte)

Bon, le plus dur reste à faire -> 2)
Depuis une heure je me casse la tête à comprendre d'où sort cette formule mais je comprends pas

Merci de bien vouloir m'expliquer

[Diamonds]

Je pense avoir une idée !
Donc on a A_k CodeCogsEqn(3).gif
et pour A_k+1 c'est la même avec k+1 au lieu de k+1 dans les deux membres.
Il me suffit de refaire la formule suivante avec eux img1.gif et normalement j'aurai la réponse attendue de l'énoncé ?

[Teddy-mension]

D'accord ! Pour A1A2 aussi je trouve le même résultat

Pas d'accord..

Bon, le plus dur reste à faire -> 2)
Depuis une heure je me casse la tête à comprendre d'où sort cette formule mais je comprends pas

Quelles sont les coordonnées de et de ? Tu en déduis donc que..

EDIT : Croisement avec ton dernier post que je n'ai pas compris..

[Diamonds]

coordonnées de Ak (k/n ; V(k/n))
coordonnées de Ak+1 (k+1/n ; V(k+1/n))

Sinon pour a1a2 pourriez-vous détailler un peu le calcul histoire que je comprenne mon erreur dans la démarche ?

[Teddy-mension]

Sinon pour a1a2 pourriez-vous détailler un peu le calcul histoire que je comprenne mon erreur dans la démarche ?

On sait que et .
On en déduit donc : .

coordonnées de Ak (k/n ; V(k/n))
coordonnées de Ak+1 ((k+1)/n ; V((k+1)/n))

Oui (avec des parenthèses), et donc

EDIT :

Il me suffit de refaire la formule suivante avec eux Pièce jointe 231961 et normalement j'aurai la réponse attendue de l'énoncé ?

Oui, normalement ! (Tes images ne s'étaient pas affichées tout à l'heure, désolé)

[pascaltech]

Bonjour,

Je n'interviendrai pas dans les formules, mais je pense que tu peux t'inspirer de la définition des B-Splines (courbes de Bézier) pour comprendre le traitement mathématique de cette courbe définie par N points entre le point origine(a=0) et le point final (a=1) qui sont les extrémités de la courbe.

Je pense qu'il s'agit d'un exercice d'approche du monde formidable de Monsieur Bézier ! Bonne balade.