Valeur d'un angle

[Argon39]

Bonjour,j'avais fait cet exxercice:
Écrire ce nombre complexe "z2=-2(1+i) sous forme trigonométrique ce qui donne :
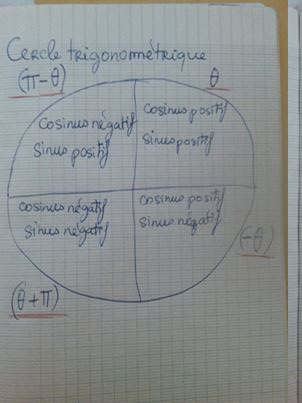
z2=2√2(-√2/2+i*-√2/2)=2√2(cos-3π/4+isin-3π/4);(ce que mon professeur à trouvé) et j'ai compris comment on trouve le module mais j'ai du mal a comprendre comment mon professeur à trouvé l'angle,parce que moi j'utilise ce cercle pour trouvé langle:


Donc normalement,pour moi,si le sinus et le cosinus sont négatif,on utilise la formule,"θ= θ+π,et comme on a deux fois √2/2 donc on sait déja que c'est un angle du type π/4 et si on applique ma formule,on a un angle égale a π/4+
4π/4=5π/4,or ce n'est pas l'angle que mon professeur à trouvé.Merci de m'aidé à comprendre pourquoi mon professeur à trouvé cet angle.
-----

[pallas]

verifie bien la position de 5pi/4 et de -3pi/4 sur le cercle trigo !! alors !!!

[Argon39]

Alors ces deux angles corespondent au même point mais et leur sinus et leur cosinus sont différent donc on ne peut pa dire que
z2=2√2(cos-3π/4+i*sin-3π/4)=2√2(cos5π/4+isin5π/4).

[gg0]

Alors ces deux angles corespondent à deux point opposé

Non !

Ce sont deux mesures du même angle puisque leur différence est 2pi (ou moins -2pi, suivant l'ordre de la soustraction).
Tu ne les as pas placés correctement. Pi fait un demi tout, 5pi/4 est un peu plus d'un demi tour, -3pi/4 un peu moins d'un demi tour dans l'autre sens, on arrive au même endroit.

Cordialement.

[A voir en vidéo sur Futura]

[Argon39]

Oui effectivement vous avez raison j'avais pris 3π/4 au lieu de -3π/4,d'ou mon erreur.
Donc j'ai le droit d'écrire que z2=2√2(cos-3π/4+i*sin-3π/4)=2√2(cos5π/4+isin5π/4) non?

Cordialement.

[gg0]

Ben ...puisque c'est le même angle !

Et pour éviter la difficulté de lecture, tu mettra les parenthèses de fonction:
z2=2√2(cos(-3π/4)+i*sin(-3π/4))=2√2(cos(5π/4)+isin(5π/4))

Cordialement.

[Argon39]

Ok,merci beaucoup pour vôtre aide.