Terminale S : limites de fonctions

[LFC7]

Bonjour bonjour ! J'ai un devoir-maison de maths à rendre pour la rentrée. Voici l'énoncé :

"Soit f la fonction définie pour f(x) = (2x² + x - 1)/(x² - 2x + 2)

1) Déterminer l'ensemble de définition de f.
2) Etudier les limites de f aux bornes de son ensemble de définition.
3) En déduire l'existence d'une asymptote D et étudier la position relative de la courbe Cf et de D.
4) Calculer f'(x)
5) Tracer le tableau de variations de f.
6) Déterminer l'équation de la tangente T à Cf au point d'abscisse a = 1
7) Tracer T, D et Cf dans un répère orthonormé.
8) Discuter graphiquement, suivant les valeurs du réel m, le nombre de solutions de l'équation (m - 2)x² - x(2m + 1) + 2m + 1 = 0.

Mon problème se pose à la question 8. Notre professeur ne nous a pas demandé de justifier par un calcul.

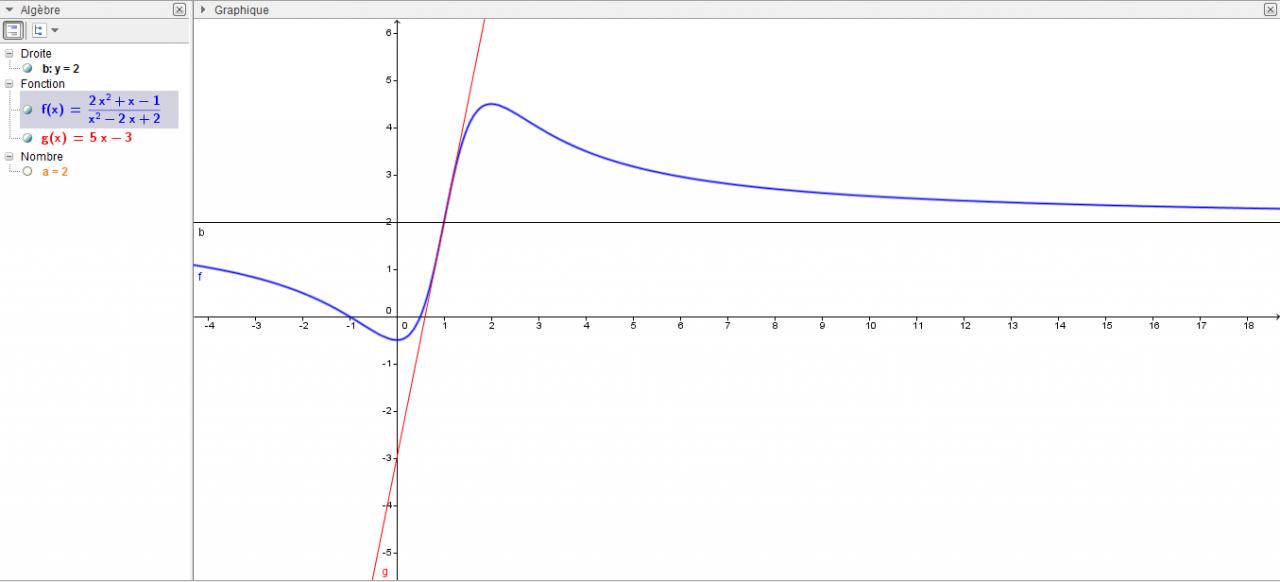
Voici le graphique représentant D, T et Cf.



Si vous pouvez m'apporter un peu d'aide, ça serait gentil ! Merci d'avance !
-----

[joel_5632]

Bonjour,

Que veux tu exactement, de l'aide pour la question 8 ?

[LFC7]

Oui, c'est ça.

[joel_5632]

et bien développe le polynome de la question 8 et mets m en facteur, tu verras apparaître les numérateur et dénominateur de f

[A voir en vidéo sur Futura]

[LFC7]

Alors :

(m - 2)x² - x(2m + 1) + 2m + 1
= mx² - 2x² - 2mx - x + 2m + 1
= m*(x² - (2x²/m) - 2x - (x/m) + 2 + (1/m))
= m*(x² - (2x²/m) 2x - (x/m) + 2 + (1/m))

Ah bah oui !! J'avais déjà essayé de développer mais je n'avais pas pensé à ça...
Et que dois-je faire après ?

[phucpham]

oh. Thank so much! LFC7

[joel_5632]

non LFC7 ce n'est pas ce qu'il fallait faire

(m - 2)x² - x(2m + 1) + 2m + 1 = m(x²-2x+2) - (2x² +x -1)

[LFC7]

Ah zut...Merci pour la solution !

Et du coup, à l'aide du graphique, je peux trouver la valeur de m telle que l'équation = 0 ? Sur le graphique, l'asymptote, la tangente et la courbe de la fonction ont une intersection en un point (appelons-le A) et ses coordoonées sont (1 ; 2). Donc m = 2 ?

[joel_5632]

Tu es ramené a déterminer selon le paramètre m le nombre de solutions de l'équation f(x) = m ce que tu devrais savoir faire grâce au graphique

[LFC7]

D'accord ! Donc l'équation f(x) = m n'a qu'une seule solution : 2. Merci beaucoup pour ton aide !

[joel_5632]

non, non.

Il faut discuter le nombre de solution de l'équation f(x)=m en fonction de m

si je te demande de me résoudre f(x) = 10 tu me trouves combien de solution (sans calcul, seulement en regardant le graphique) ?

[LFC7]

D'après le graphique, on trouve 1 solution.

[joel_5632]

Et bien moi je n'en vois aucune.

Toute la courbe Cf est comprise entre y=4.5 et y=-0.5 à peu près, il n'y a aucun x tel que f(x)=10

[LFC7]

Ah oui, je me suis trompée, dans ma tête j'ai compris qu'il fallait résoudre f(10)...
Du coup, pour en revenir à f(x) = 0, je vois 2 solutions.

[joel_5632]

oui
pour f(x) = 0 , deux solution
f(x) = 10) pas de solution

Maintenant il faut discuter en fonction de m

si m>4.5 pas de solutions
si m=4.5 une seule solution
si 2<m<4.5 deux solutions

etc à continuer

Tu peux vérifier par le calcul même si ce n'est pas demandé en calculant le discriminant delta qui est un trinome du 2 ème degré en m, puis en étudiant le signe de ce trinome, ce qui nécessite encore un calcul de discriminant (et là des élèves sont parfois perdus ...). Avec cette méthode calculatoire il faut mettre à part le cas m=2 dans avec m=2 on n'a plus une équation du 2ème degré mais du 1er degré.

[LFC7]

2<m<4,5 : c'est là où la tangente et Cf se confondent.

La suite :
Si 0,1 (environ) < m <4,5 ; l'équation a deux solutions.
Si m <0,1; l'équation n'a pas de solution.

C'est ça ?

[joel_5632]

> Si 0,1 (environ) < m <4,5 ; l'équation a deux solutions.

Pourquoi 0.1 ?

moi je vois: -0.5 < m < 4.5 et m \= 2 deux solutions
si m=2 une seule solution
si m=4.5 une seule solution
si m= -0.5 une seule solution

et si m > 4.5 ou m < -0.5 aucune solution

[LFC7]

Ah oui, je me suis trompée...

"m \= 2" c'est m différent de 2 ou m inférieur ou égal à 2 ?

[joel_5632]

m différent de 2

[LFC7]

D'accord ! Je crois avoir compris. Merci énormément pour ton aide !