Valeures absolues avec second degrès et fonctions

[davidtj]

Bonjour, j'aimerai savoir quelque petits trucs à propos de mon devoir maison à rendre dans 2 semaine.
Je vous présente le sujet
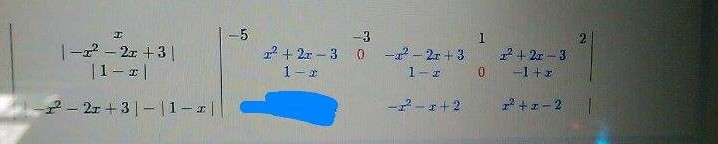
On considère la fonction définie par f(x)= /-x²-2x+3/-/1-x/ sur l'intervalle [-5;2]

1) Écrire f sans barre de valeur absolue.


Donc f(x) = (-x²-2x+3)-(1-x) si -x²-2x+3-1+x > ou égale à 0
= -x²-2x+3-1+x
= -x²-x+2
ou f(x)= -(-x²-2x+3-1)-(-(1-x)) si x²+2x-3+1-x < ou égale à 0
= x²+2x-3+1-x
=x²+x-2
Est-ce bon s'il vous plait???

2) Étudier les variations de la fonction f et en dresser le tableau

Ici je sais qu'il faut que je calcule les racines de la fonctions avec DELTA= b²-4ac et x1 et x2 sauf que je sais pas comment placer tout cela dans un tableau ... En étudiant la fonction je peux dire que sa fait une bosse ou il y a des valeur négative puis positive puis négative.
J'ai fait ceci

-x²-2x+3=0 Donc c'est une équation où l'on peux trouver les racines grâce à Delta= b²-4ac
=(-2)²-4*(-1)*3
= 4+4*3
= 16 comme delta est plus grand que 0 alors
X1= (-b²-racine de delta)/2 X2 = (-b²+ racine de delta)/2
=(-(-2)²-4)/2 =8/-2 = -4
= (4-4)/2 = 0

Donc l'équation a deux solution tel que 0 et 4
Pareille avec les autres termes
1-x où delta = 1 donc deux solution ou X1 et X2= 0 (c'est bizzard j'ai un doute)

x²+2x-3 où delta = 16 et X1= -3 avec X2 = 1 (signe de a sauf entre ces racines donc cela fait une courbe creuse avec des valeurs positive négative puis positive)

Puis -1+x pareille que 1-x

-x²-x+2 où DELTA = 9 X1= 1 et X2= -2

x²+x-2 où DELTA= 9 X1= -2 et X2= 1

3) Tracer la représentation graphique de la fonction f

Sa j'en n'est aucune idée mais je vais essayer de regarder sur internet et si vous pouvez m'aider

4) Résoudre l'inéquation f(x) < ou égale à -x+1

Je sais qu'il faut passer des termes dans un autre en prenant un point quelconque.

Merci de bien vouloir prendre un peux de votre temps si possible pour m'aider car j'aimerai vraiment comprendre vue que j'en aurais tout au long de cette année des valeurs absolue et du second degrès
-----

[gg0]

Bonjour.

Ta fonction est bien f(x)= |-x²-2x+3| - |1-x| ? (sur un clavier classique, | s'obtient avec AltGr 6)
dans ce cas, il y a deux valeurs absolues à traiter. Et si tu ne dis pas dans quel cas on a telle ou telle quantité compliquée qui est positive, tu n'as rien fait.
Donc tu dois étudier les signes de -x²-2x+3 et de 1-x, puis déterminer des intervalles de valeurs de x sur lesquels on peut enlever les valeurs absolues.

Bon travail !

[PlaneteF]

Bonsoir,

Donc f(x) = (-x²-2x+3)-(1-x) si -x²-2x+3-1+x > ou égale à 0
(...)
ou f(x)= -(-x²-2x+3-1)-(-(1-x)) si x²+2x-3+1-x < ou égale à 0

Non c'est complétement faux ce que tu écris là, ... attention à ne pas confondre (ton énoncé) avec (ce que tu considères) ... ce n'est pas du tout la même chose.

Cordialement

[davidtj]

Oui j'ai définis mes intervalles:

-x²-2x+3 si x dans [-3 ; 1]

x²+2x-3 si x dans [-5;-3][1 ; 2]

1-x si x dans [-5 ; 1]

-1+x si x dans [1 ; 2]

[A voir en vidéo sur Futura]

[davidtj]

Par contre je ne comprend pas se que j'ai fais de faux ? vous me l'avais dis mais je n'es pas bien compris

[gg0]

Ben ... tu avais mélangé les deux sans tenir compte de l'énoncé.

Maintenant, il te reste à écrire f sans les valeurs absolues :
Si x dans [-5,-3], f(x)= ...
Si x dans [-3,-1], f(x)= ...
etc.

Cordialement.

Nb : Que de fautes : "Par contre je ne comprends pas ce que j'ai fait de faux ? Vous me l'avez dit mais je n'ai pas bien compris." Ce qu'on écrit de travers, on le comprend mal !!

[davidtj]

Excuser moi..

Alors pour cela on m'a aidé à faire un tableau de variation et sa a donné ceci

X -5 -3 1 2

|-X²-2X+3| X²+2X-3 0 -X²-2X+3 X²+2X-3

|1-X| 1-X 1-X 0 -1+X

|-X²-2X+3|-|1-X| ?????? -X²-X+2 X²+X-2

[davidtj]

justement j'ai fais un tableau de signe aidé par ma soeur sauf que je sais pas qu'est ce qui se trouve sous la partie bleu

[PlaneteF]

Bonjour,

justement j'ai fais un tableau de signe aidé par ma soeur sauf que je sais pas qu'est ce qui se trouve sous la partie bleu Pièce jointe 298445

Et comment as-tu fait pour remplir les autres parties ?! ... Où est la différence ? ... C'est à se demander si tu comprends ce que tu fais.

Cordialement

[davidtj]

Les autres sortent de la fonctions générale que j'ai séparé en deux (selon x< ou x>, dsl j'ai du mal à m'exprimer) où j'ai calculer leur racines donc c'est pour cela que j'ai réussi à trouver leur intervalles. Mon problème c'est que je ne comprends pas comme vous dite se que je fais mais je me base sur les leçons apprises par coeur et des exercices qui pourraient se rapprocher de celui-ci. Mais c'est bon j'ai trouver en faite c'est x²-3x+4 car on soustrait la second ligne du tableau à la première se qui nous donne toutes les autres expressions que j'ai cité dans mon tableau. Mais j'aimerai savoir si c'est bien le tableau de variation que l'on me demande de faire ?

[gg0]

C'est un tableau, qui donne l'expression de la fonction. Donc pas un tableau de signe, puisqu'on n'y met pas des signes.