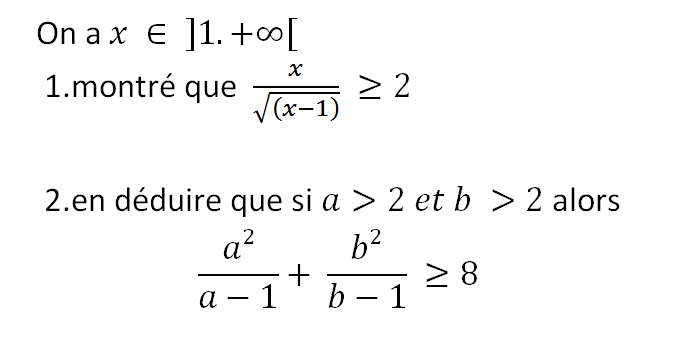SALUT je voulais savoir comment résoudre cet encadrement SVP !On a
-----
Répondre à la discussion
Affichage des résultats 1 à 13 sur 13
On a x ∈ ]1.+∞[ montrer que ( x/√(x-1) )≥ 2
- 29/12/2015, 14h54 #1invited38ca94b
On a x ∈ ]1.+∞[ montrer que ( x/√(x-1) )≥ 2
------
-----
- 29/12/2015, 15h24 #2gg0Animateur Mathématiques
Re : On a x ∈ ]1.+∞[ montrer que ( x/√(x-1) )≥ 2
Bonjour.
Qu'as-tu essayé ?
- 29/12/2015, 20h56 #3PlaneteF
Re : On a x ∈ ]1.+∞[ montrer que ( x/√(x-1) )≥ 2
Bonsoir,
Il n'y a pas d' "encadrement" à "résoudre", mais 2 inégalités à démontrer.
Envoyé par anass8 
CordialementDernière modification par PlaneteF ; 29/12/2015 à 20h59.
- 29/12/2015, 22h20 #4invited38ca94b
Re : On a x ∈ ]1.+∞[ montrer que ( x/√(x-1) )≥ 2
comment pouvons le faire ?? svp
- Aujourd'huiA voir en vidéo sur Futura
- 29/12/2015, 22h21 #5invited38ca94b
Re : On a x ∈ ]1.+∞[ montrer que ( x/√(x-1) )≥ 2
franchement j'ai pas pu savoir d'où commencer Envoyé par gg0
- 29/12/2015, 23h05 #6invite184b87fd
Re : On a x ∈ ]1.+∞[ montrer que ( x/√(x-1) )≥ 2
Bonsoir
tu peux essayer de raisonner par équivalence en partant de ta première inéquation .
Tu arriveras à une inéquation avec un polynôme et tu pourras facilement démontrer ta propriété .
cdt
- 29/12/2015, 23h34 #7invite51d17075Animateur Mathématiques
Re : On a x ∈ ]1.+∞[ montrer que ( x/√(x-1) )≥ 2
pour la première , vu ton domaine de def tous les termes de l'inégalité sont >0
tu peux mettre tout au carré et ensuite passer le ( x-1) de l'autre coté au numérateur.
après, je te laisse faire.
- 30/12/2015, 09h28 #8gg0Animateur Mathématiques
Re : On a x ∈ ]1.+∞[ montrer que ( x/√(x-1) )≥ 2
Pour l'instant, Anass8 n'a rien produit, il se contente d'attendre qu'on fasse son travail !!!!:
- 30/12/2015, 10h59 #9invite51d17075Animateur Mathématiques
Re : On a x ∈ ]1.+∞[ montrer que ( x/√(x-1) )≥ 2
c'est exact, et on a parfois des "surprises" avec certains nouveaux qui se comportent en poseurs de casiers pour crustacés.
mais son dernier mess date d'hier à 22h21.
alors on verra.
Cdt
- 30/12/2015, 14h10 #10invited38ca94b
Re : On a x ∈ ]1.+∞[ montrer que ( x/√(x-1) )≥ 2
si j'ai bien compris on doit au début qu'on met tout au carré
- 30/12/2015, 16h00 #11invite51d17075Animateur Mathématiques
Re : On a x ∈ ]1.+∞[ montrer que ( x/√(x-1) )≥ 2
et c'est tout ?
déjà mes indications allaient plus loin.
- 30/12/2015, 16h49 #12invite184b87fd
Re : On a x ∈ ]1.+∞[ montrer que ( x/√(x-1) )≥ 2
tu dois obtenir un polynôme comme l'avait suggéré ansset dans ton inéquation .
Ensuite il te faut étudier ton polynôme pour pouvoir conclure .
cdt
- 30/12/2015, 16h53 #13invite51d17075Animateur Mathématiques
Re : On a x ∈ ]1.+∞[ montrer que ( x/√(x-1) )≥ 2
tu l'avais aussi mentionné.
mais il semble que annas8 ait un gros poil dans la main.
Discussions similaires
-
Prouver que Σ(1/k)*Σ(k) ≥ n²
Par inviteabaf03e3 dans le forum Mathématiques du supérieurRéponses: 7Dernier message: 14/09/2015, 21h23 -
√(4m) = 2√m ???? avec m c métre
Par invite34af0f06 dans le forum Mathématiques du supérieurRéponses: 4Dernier message: 28/12/2014, 08h16 -
Limite de ln(x)/√x en + ∞
Par invite82aea940 dans le forum Mathématiques du collège et du lycéeRéponses: 2Dernier message: 26/01/2014, 10h18 -
Lever une indétermination de la forme ∞/∞
Par invite51a9f393 dans le forum Mathématiques du supérieurRéponses: 2Dernier message: 30/10/2011, 13h28 -
Petite question sur les limites en +∞ ou -∞...
Par invitede11adb2 dans le forum Mathématiques du collège et du lycéeRéponses: 7Dernier message: 06/02/2008, 17h44