problème à résoudre sur la force centrifuge

[skrz74]

Bonjour,
je suis en terminale STI2D option ITEC et comme projet, nous avons choisis de réaliser un phare directionnel s'orientant avec la force centrifuge.
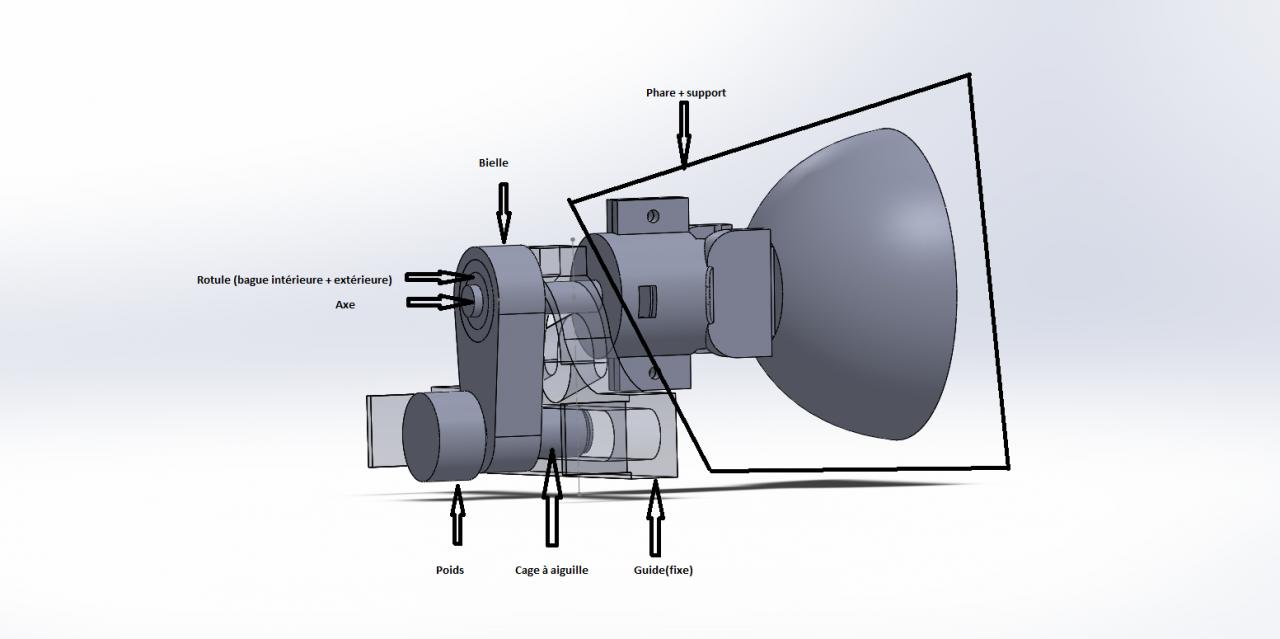
En partant de là, nous avons crée un mécanisme qui "reçoit" la force centrifuge, la transmet à notre phare grâce à une bielle qui se charge de l'orientation.
seulement, je ne sais pas calculer la force centrifuge dans notre mécanisme, celui-ci prévoit un guide (droit) qui se charge de diriger la masse qui reçoit la force centrifuge, or, sur une route sans virage, ce guide est à l'horizontale (par rapport à la route) mais dans les virages, il s'incline et mon but est de déterminer l'énergie (liée à la force centrifuge) qui s'appliquera à la masse dans ce cas là.
nous avons calculé que pour la masse, la force centrifuge s'exerçant dessus serait de 2.4N

si vous voulez, pour mieux vous exposer mon problème, j'ai des schémas fait sur solidworks afin que vous compreniez mieux comment marche le mécanisme.

merci de votre lecture et de vos conseils
-----

[pierre2121]

Je veux bien

[Dynamix]

Moi aussi parce que là c' est incompréhensible .
Voir ce phare , même en dessin , nous éclairerait .

Tu ne confonds pas force centrifuge et effet gyroscopique ?

[pierre2121]

Je peux bien te dire que la force qui s'exerce sur un solide en rotation autour d'un axe est une accélération centripète de valeur v^2/R mais la force centrifuge je ne connais pas ce mot (dans nos cours sa passe toujours par des noms bizarre qui je me convienne pas ^_^ )

[A voir en vidéo sur Futura]

[skrz74]

je vous envoie tout ça demain matin, en tout cas merci de vos réponses

[skrz74]

Pour ceux qui aurait du mal à voir, voici le lien d'un hébergeur d'image avec la photo en question: http://hpics.li/5601c7e
Le phare sera fixé sur une liaison rotule, c'est donc comme si il était fixe en son centre (on lui empêche la translation avant-arrière).
Du coup, ce que je souhaite déterminer, c'est la force qui s'exercera sur le poids quand la moto n'est pas verticale par rapport à la route (dans les virages), ce qui me permettra de savoir si la force centrifuge sera plus grande que la force d'attraction gravitationelle au niveau du poids.

Pour répondre à Dynamix, je parle bien de force centrifuge et non de l'effet gyroscopique.

[Cotissois31]

Dans le référentiel de la moto, la masse va bouger dans les virages. Tant qu'elle a la possibilité, la masse va le faire à une accélération répondant à somme des forces (incluant centrifuge et frottement lié au roulement) = m.a, avec a accélération relative.
Au cours de son déplacement, la masse acquiert donc une vitesse relative qui s'ajoute à la vitesse de la moto. L'énergie cinétique est 1/2 m v² avec v vitesse totale = relative + moto
Lorsque la masse touche la fin du guide, elle a uniquement l'énergie cinétique de la moto car la vitesse relative repasse à zéro.

Pour les physiciens, on ne parle pas de force centrifuge mais de simple inertie. Dans un mouvement en rotation, une force centripète oblige la rotation (accélération centripète). L'inertie "centrifuge" en ligne droite se manifeste uniquement si la force centripète s'arrête. La force centrifuge est alors juste un artifice de calcul.

Pour les mécaniciens, une masse en rotation grâce à un axe nous dit que la liaison entre la masse et l'axe subit l'opposé de la force centripète, donc une force centrifuge. Si la liaison ce sont nos doigts qui entourent la poignée d'un marteau d'athlétisme, on ressent la force centrifuge qui s'applique très nettement sur la liaison, tendant à écarter la poignée des doigts... Au sens strict, ce n'est pas la masse qui subit la force centrifuge, mais la liaison.

[skrz74]

merci beaucoup de ton explication, donc pour la force qui s'exerce (seulement sur ce qui "peut bouger"? donc la liaison (ensemble bielle, poids, rotule)? ) est égale à la somme de la force centrifuge et de l’énergie cinétique? et lorsqu'elle atteint la fin du guide, il n'y a plus que la force centrifuge qui s'exerce sur cette liaison?

[Cotissois31]

J'ai cru que vous vouliez des considérations énergétiques. Si c'est seulement la force, on n'ajoute pas une force et une énergie.

Ce qui complique ici, c'est qu'il y a deux plans de rotation. Le plan de la bielle et le plan de la route. Il faut donc être prudent sur le mot "centrifuge".

Dans un cas sans frottement (liaisons parfaites, bielle de masse négligeable, pas de guide), dans le repère de la bielle (pour simplifier, car on a alors somme des forces = 0 sur la masse)

En ligne droite, la masse subit son poids P et une force de liaison F=P, telle un pendule statique.
Dans le virage, la masse subit son poids P, une force de liaison F et une pseudo force centrifuge Fc (vers l'extérieur de la courbe de la route). Les trois se compensent (somme des forces = 0), ce qui permet de calculer F.

F force de liaison est aussi la force qui s'exerce sur le bas de la bielle, dans le sens opposé (elle tire sur la bielle). Si cette force est non-colinéaire à la bielle, alors une rotation se produit, je pense que c'est ceci qui est important. Il est conseillé alors de calculer le moment de F par rapport à la liaison pivot (rotule) plutôt que le simple module de F.

Le vecteur F, donc son moment, va dépendre de la masse, du rayon de courbure et de la vitesse de la moto.

[skrz74]

merci beaucoup pour vos explications,
cependant, je n'ai pas bien compris la liaison F que vous décrivez, j'ai un peu de mal du coup à comprendre comment faire la somme des moments...

[skrz74]

désolé du double post mais j'ai une autre question, et je ne sais pas comment modifier mon message précédent...
si on exerce une force horizontale sur un objet et que celui-ci est contraint de suivre un guide, est ce que si le guide n'est pas dans la même direction on perd une partie de la force?
c'est pas très clair du coup je vais vous faire un exemple: je pousse une bille et ma force est dirigée de manière horizontale mais ma bille est obligée de suivre le guide qui est penché à 20° (sens trigo) de mon effort, est ce que je perdrais une partie de la force (même si le coefficient de frottement est ma bille et mon guide est nul) ??

[Dynamix]

je pousse une bille et ma force est dirigée de manière horizontale mais ma bille est obligée de suivre le guide qui est penché à 20° (sens trigo) de mon effort, est ce que je perdrais une partie de la force (même si le coefficient de frottement est ma bille et mon guide est nul) ??

En terminale STI tu devrais savoir résoudre ce problème .
Cherche un peu .

[skrz74]

En terminale STI tu devrais savoir résoudre ce problème .
Cherche un peu .

Bah pour moi on devrait perdre seulement l'énergie potentielle du fait de la hauteur qui augmente, je me trompe?

[Cotissois31]

J'ai sans doute compliqué précédemment, car sur ce type de problème, on considère une réaction dans l'axe. La résultante des forces sur la masse est forcément perpendiculaire à l'axe, donc agissant comme le couple.
Ce qui se passe précisément au niveau de la liaison est secondaire tant que la liaison est rigide donc... "solide".

Sur ce problème, en oubliant le guide et le roulement associé, la masse subit :
- une réaction dans l'axe de la bielle
- le poids
- la pseudo force centrifuge (horizontale, vers l'extérieur du virage)

A l'équilibre vertical, pas d'effet centrifuge : la réaction égale le poids, dans le sens opposé. Le poids vers le bas, la réaction vers le haut.

Lors du virage, la masse subit un effet centrifuge horizontal. La bielle force un mouvement circulaire vertical de la masse donc la résultante sera forcément perpendiculaire à la bielle.
La résultante des forces sur la masse, de par la liaison masse-bielle co-localisée (à peu près) avec la masse, devient une force qui s'exerce sur le bas de la bielle, toujours perpendiculaire, donc déterminant le couple exercé.

Ce qui est lié directement à la masse, c'est uniquement le poids et la pseudo force centrifuge, mais n'est-ce pas le couple agissant sur la bielle que l'on cherche à calculer ?

[skrz74]

J'ai sans doute compliqué précédemment, car sur ce type de problème, on considère une réaction dans l'axe. La résultante des forces sur la masse est forcément perpendiculaire à l'axe, donc agissant comme le couple.
Ce qui se passe précisément au niveau de la liaison est secondaire tant que la liaison est rigide donc... "solide".

Sur ce problème, en oubliant le guide et le roulement associé, la masse subit :
- une réaction dans l'axe de la bielle
- le poids
- la pseudo force centrifuge (horizontale, vers l'extérieur du virage)

A l'équilibre vertical, pas d'effet centrifuge : la réaction égale le poids, dans le sens opposé. Le poids vers le bas, la réaction vers le haut.

Lors du virage, la masse subit un effet centrifuge horizontal. La bielle force un mouvement circulaire vertical de la masse donc la résultante sera forcément perpendiculaire à la bielle.
La résultante des forces sur la masse, de par la liaison masse-bielle co-localisée (à peu près) avec la masse, devient une force qui s'exerce sur le bas de la bielle, toujours perpendiculaire, donc déterminant le couple exercé.

Ce qui est lié directement à la masse, c'est uniquement le poids et la pseudo force centrifuge, mais n'est-ce pas le couple agissant sur la bielle que l'on cherche à calculer ?

Merci pour votre réponse construite.
Bah je pensais plutôt avoir à chercher une force, je ne vois pas bien comment calculer le couple car je ne vois pas bien quelle distances vous voudriez prendre?

[Cotissois31]

Pour expliquer une rotation d'un solide, on doit toujours faire intervenir un couple.
La force ne permet d'expliquer que le mouvement des objets ponctuels (mécanique du point)

Ici, l'équivalence est rapide : le couple sur la bielle est le moment de F, résultante des forces sur la masse, par rapport au pivot de la bielle. Ce couple est fonction du rayon R (longueur de la bielle)
Plus R est grand, plus le couple est important, évidemment.

En terme énergétique, la pseudo force centrifuge travaille d'autant plus pour la rotation que la masse a un faible déplacement vertical. Plus R est grand, plus on augmente la possibilité de faire travailler la pseudo force centrifuge car le déplacement vertical demandera une grande distance horizontale.
Ceci est vrai tant que la bielle a une masse négligeable donc c'est un peu théorique.

[Dynamix]

Pour expliquer une rotation d'un solide, on doit toujours faire intervenir un couple.

Quel couple explique , par exemple , la rotation de la terre ?
Le couple ou plutôt le moment "explique" l' accélération angulaire .

La force ne permet d'expliquer que le mouvement des objets ponctuels (mécanique du point)

La force (la résultante) "explique" l' accélération en translation d' un solide aussi bien que d' un théorique point matériel

[Cotissois31]

Sur le 1, c'était pour écrire rapidement.

Sur le 2, en effet. Le fait est qu'on considère essentiellement la translation comme un problème ponctuel ramené au centre d'inertie.

[Dynamix]

Je ne vois pas la nécessité de répondre rapidement à quelqu'un qui ne fait pas d' effort pour expliquer son problème

[Cotissois31]

Pour être précis aussi, le couple existe bien en tant que grandeur spécifique. Le moment d'une force n'est qu'un outil intervenant dans le calcul du couple.

couple = somme des moments appliqués par rapport au centre d'inertie, en supposant qu'il y a au minimum 2 moments.

La liaison pivot idéale est un cas très particulier. On considère le moment de la réaction de liaison, pour justifier l'existence d'un couple, mais on néglige son travail, de telle sorte que le couple est fourni entièrement par le moment extérieur. Physiquement, il y a toujours deux moments (par rapport au centre d'inertie) sur un axe en liaison pivot même si la formule donne l'impression d'un seul moment (qui est en fait par rapport au pivot)

[Dynamix]

Pour être précis aussi, le couple existe bien en tant que grandeur spécifique. Le moment d'une force n'est qu'un outil intervenant dans le calcul du couple.
couple = somme des moments appliqués par rapport au centre d'inertie, en supposant qu'il y a au minimum 2 moments.

Théorie très personnelle .
Le couple est en fait un cas particulier .
Dans le cas général on parle de moment .
https://fr.wikipedia.org/wiki/Torseur_statique

[skrz74]

Du coup, je reformule ma question:
je voulais savoir comment calculer la "résultante" d'une force qui n'a pas le même angle (je ne sais pas trop si c'est français) et surtout si c'était possible,
par rapport à la force nominale (dans mon cas, c'est la force centrifuge qui est horizontale) qui s'applique sur un solide, mais la trajectoire du solide est guidée par un guide qui à une inclinaison de 5° vers le haut, comment calculer la résultante (parallèle au guide) qui s'appliquera au solide?
je pensais que la résultante serait égale à la force nominale - les efforts - la différence de potentiel (une partie de la force servira à faire monter le solide) mais je ne suis sur de rien.

la encore, je sais pas si vous comprendrez très bien, du coup je peux faire des schémas pour que vous compreniez mieux ma question.

[Cotissois31]

Après réduction, le couple est la somme de deux moments égaux, par rapport au centre d'inertie. Ce que l'on simplifie en "moment du couple".

Le "moment du couple" est une expression, mais de façon générale le couple est un concept énergétique précis alors que le moment est une propriété géométrique d'une force par rapport à un point quelconque.

[Cotissois31]

Si je ne me trompe pas, décider que le guide a une orientation donnée risque de tout bloquer pour un déplacement critique de la masse. C'est alors un simple problème de cinématique (géométrique) lié à la géométrie du guide, du roulement, et le déplacement théorique de la masse.

L'effet du guide c'est de compenser un degré de liberté avant-arrière mal contrôlé sur le pivot ou de freiner la masse ?

Si c'est un frein sur la masse, c'est que le guide doit être optimisé pour être dans la trajectoire de la masse, donc son orientation est à déduire et pas à imposer.

Si c'est un degré avant-arrière, je comprendrais mal un cage à aiguilles car le frottement va s'exercer vers l'avant ou l'arrière, pas de gauche à droite.

[Dynamix]

le couple est la somme de deux moments égaux
le couple est un concept énergétique

Tout ça sent la théorie personnelle .
A moins que tu n' ais des références , il faut cesser de raconter n' importe quoi .

[skrz74]

Si je ne me trompe pas, décider que le guide a une orientation donnée risque de tout bloquer pour un déplacement critique de la masse. C'est alors un simple problème de cinématique (géométrique) lié à la géométrie du guide, du roulement, et le déplacement théorique de la masse.

L'effet du guide c'est de compenser un degré de liberté avant-arrière mal contrôlé sur le pivot ou de freiner la masse ?

Si c'est un frein sur la masse, c'est que le guide doit être optimisé pour être dans la trajectoire de la masse, donc son orientation est à déduire et pas à imposer.

Si c'est un degré avant-arrière, je comprendrais mal un cage à aiguilles car le frottement va s'exercer vers l'avant ou l'arrière, pas de gauche à droite.

Pour nous, le guide du bas est "moteur" du guide du haut, car il sert à contrôler la trajectoire de la bielle et l'envoie vers l'extérieur du virage avec la force centrifuge, ce qui fait pencher le haut de la bielle grâce à l'axe qui passe dans le guide du haut. La cage à aiguille est la simplement pour réduire les frottements, qui réduiront considérablement la force qui emmène la bielle vers l'extérieur.

[Cotissois31]

J'ai compris d'où vient notre désacord Dynamix.

J'ai considéré uniquement la partie rotation de la bielle, et pas le déplacement de son centre d'inertie. Ceci explique pourquoi vous parlez seulement de moment alors que je parlais de couple et pourquoi j'arrivais à des forces virtuelles sur les liaisons. En pratique, en mécanique, toute rotation finit généralement en couple, d'où l'abus...

Après, sur le lien énergétique, il est d'usage de dire "fournir un couple" alors qu'on ne dit pas "fournir un moment". Le terme "moment" ne suffit pas en lui-même, alors que le mot "couple", oui.


Pour notre ami, faisons simple :
La valeur finale qui nous intéresse, c'est le couple fourni sur l'axe de transmission vers le phare. Dans un cas bien simplifié, il est égal au moment de F par rapport au pivot où F est la résultante des forces sur la masse soumise à l'effet centrifuge, son poids et la réaction de l'axe.

Pour le guide et le roulement associé, je dois revoir car je n'imaginais pas une telle complexité, je n'avais pas vu de guide haut d'ailleurs.

Je précise que j'essaie d'aider notre ami tout en réfléchissant un peu par moi-même, je ne fais pas ça tous les jours...

[Cotissois31]

J'ai compris d'où vient notre désacord Dynamix.

J'ai considéré uniquement la partie rotation de la bielle, et pas le déplacement de son centre d'inertie. Ceci explique pourquoi vous parlez seulement de moment alors que je parlais de couple. En pratique, en mécanique, toute rotation finit généralement en couple, d'où l'abus...

Après, sur le lien énergétique, il est d'usage de dire "fournir un couple" alors qu'on ne dit pas "fournir un moment". Le terme "moment" ne suffit pas en lui-même, alors que le mot "couple", oui.


Pour notre ami, faisons simple.
La valeur finale qui nous intéresse, c'est le couple fourni sur l'axe de transmission vers le phare. Dans un cas bien simplifié, il est égal au moment de F par rapport au pivot où F est la résultante des forces sur la masse soumise à l'effet centrifuge, son poids et la réaction de l'axe.

Pour le guide et le roulement associé, je dois revoir car je n'imaginais pas une telle complexité, je n'avais pas vu de guide haut d'ailleurs.

Je précise que j'essaie d'aider notre ami tout en réfléchissant un peu par moi-même, je ne fais pas ça tous les jours...

[skrz74]

j'ai une petite question aussi,
nous utiliserons un ressort pour remettre en place la bielle, mais je sais pas trop comment faire pour trouver la force qu'il devrait donner à la bielle pour qu'elle revienne en position "haute".. car il y aura très peu de frottements et que le poids n'influe pas sur une direction horizontale.
je précise qu'il y aura 2 ressorts de compression identiques de chaque coté du guide du bas, qui recevront une partie de la force centrifuge que leur transmet la bielle, ils seront parallèles au guide du bas.

[Dynamix]

Je n' ais toujours pas compris ton système .
Vu le peu d' information , c' est assez normal
Je ne vois surtout pas comment la force centrifuge pourrais avoir une quelconque action dans le référentiel moto .
Si tu regardes l' image post 9 du lien que je te met , tu constates que la force que "voit" le motard (ou ton système) , c' est la force verte .
Cette force est orienté presque en Z moto avec une petite composante vers l' intérieur du virage .
Ta bielle ou je ne sais quoi va s' orienter comme la force verte .
http://forums.moto-station.com/la-mo...on-dangle.html