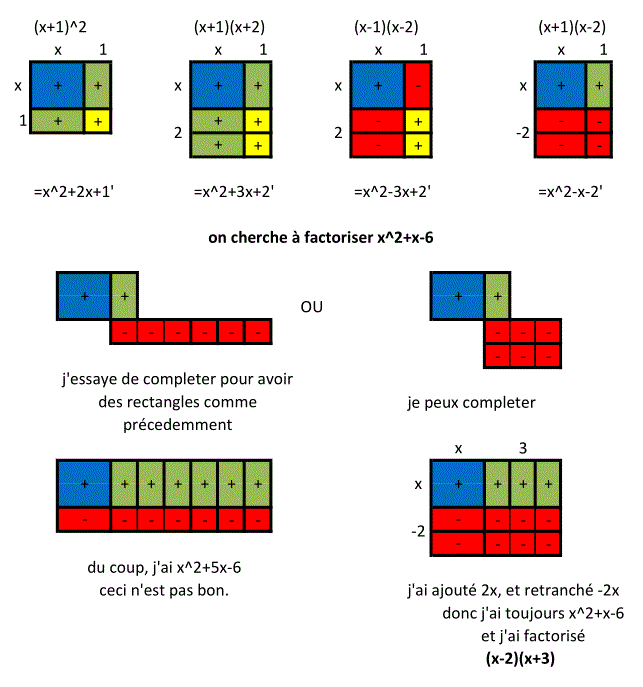
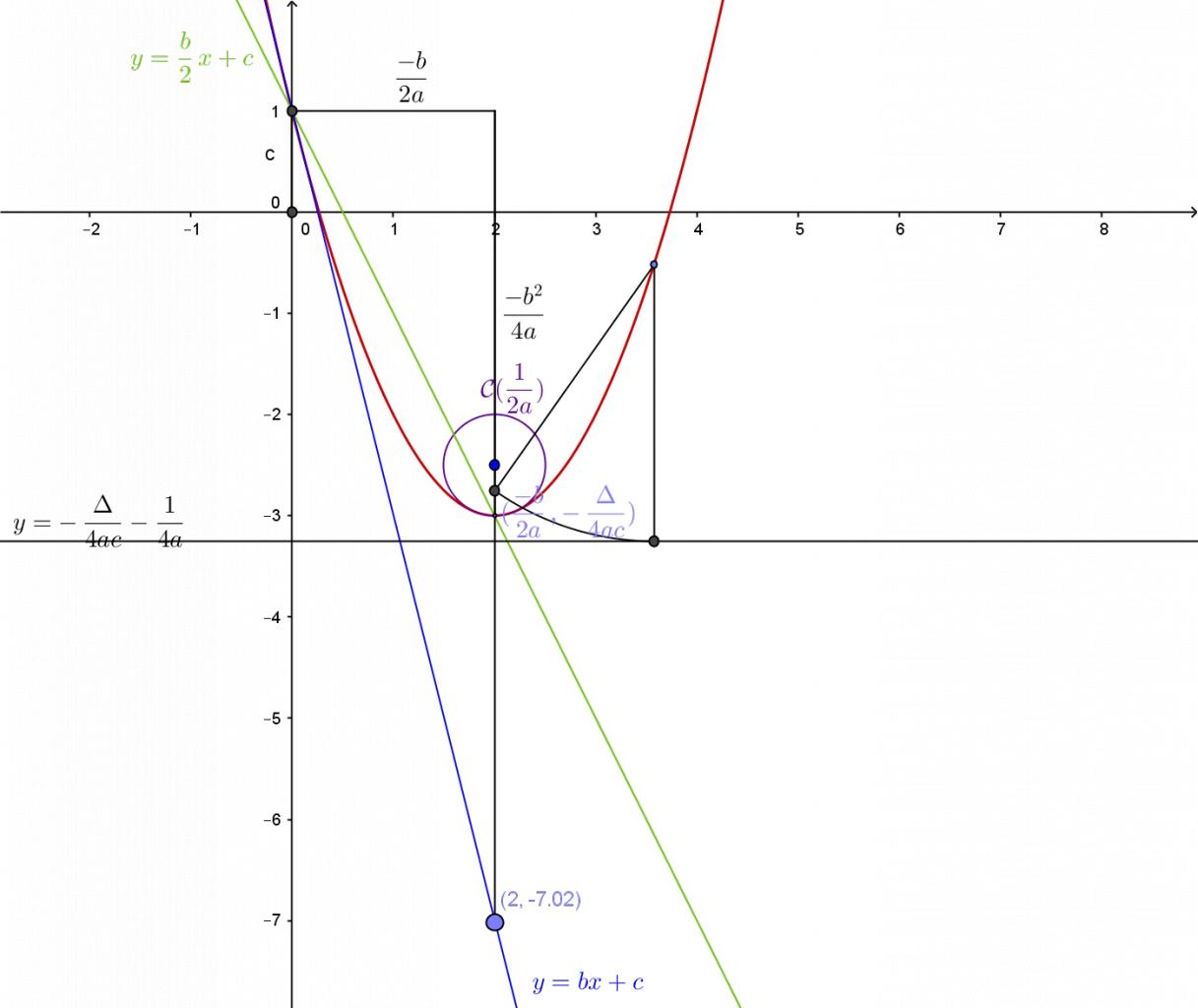
Equation second degré: Différentes méthodes et "balance"
Discussions similaires
-
Par invite5ea368ff dans le forum Programmation et langages, Algorithmique
Réponses: 1
Dernier message: 14/12/2015, 13h45
-
Par invite1f96e65c dans le forum Mathématiques du collège et du lycée
Réponses: 1
Dernier message: 25/11/2012, 19h01
-
Par invite36d5b9cf dans le forum Chimie
Réponses: 1
Dernier message: 07/02/2010, 19h35
-
Par invite17a570c1 dans le forum Biologie
Réponses: 10
Dernier message: 12/05/2008, 12h13
-
Par invite8f20fe72 dans le forum Chimie
Réponses: 5
Dernier message: 08/01/2006, 20h22