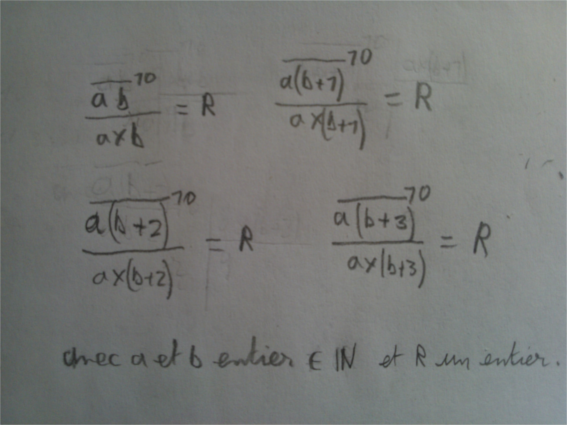Exercice de Sp maths en TS: Nombres prodigieux

[Magyo Zatura]

Bonjour à tous !

Pour les amateurs de maths qui aime aider les débutants tel que je suis !

Voici l’énoncé de l'exo :

Un nombre est appelé prodigieux s'il est divisible par le produit de ses chiffres non nuls (écrit en base de 10)

Question :

1). Montrer que nous vivons dans une année prodigieuse !
2). Trouver le plus petit entier prodigieux supérieur à 2016 qui ne contient aucun chiffre 0.
3). Trouver quatre entiers consécutif prodigieux et strictement supérieur à 10. Expliquer votre démarche.

Réponse :

1). 2016 / (2*1*6) = 2016/12 = 168
2). 2112 / (2*1*1*2) = 2112 / 4 = 528
3). Snif... Je n'y arrive vraiment pas...

De ce que j'ai compris :



Mais après je ne sais vraiment pas comment faire pour arriver à bout de la question...

Un petit coup de pouce serais vraiment parfait ! Je ne demande pas qu'on me donne la réponse ! Mais juste qu'on m'oriente sur le bon chemin car c'est pire que la jungle dans ma tête !

Merci d'avance !

Magyo
-----

[zenxbear]

c'est pas les mêmes R.

en tout cas la méthode la plus cheap serait de fabriquer un entier avec que des 1 pour les chiffres qui ne sont pas ceux des unités.
de telle sorte que le produit des chiffres non nuls correspond au chiffre des unités à une exception.

[RoBeRTo-BeNDeR]

Bonjour,

mon idée pour ta dernière question; en partant de 1,2,3 et 4 prodigieux, chercher si parmi 11, 12,13,14 ou 111,112,113,114, ou 1111,..., ou 11111,... etc... il n'y aurait pas une famille correspondant, cela devrait ne pas être trop dur. (La réponse est évidente; la seule vraie condition de succès est que le nombre de la forme 1...13 soit bien divisible par 3).

EDIT - Même idée de zenxbear. Mea culpa

[zenxbear]

malheureusement 1111...114 n'est pas divisible par 4. mais si il cherche 0, 1, 2 et 3. c'est trivial.

[A voir en vidéo sur Futura]

[RoBeRTo-BeNDeR]

Ah oui mince... oui avec 0 c'est plus simple.

(la boulette).

[Magyo Zatura]

Merci a vous deux !

Nous savons donc que 10(base10)/1; 11(base10)/1; 12(base10)/2 sont = à un entier (différent pour chacun) (Car tout est divisible pas 1 et tout chiffre se terminant par 2 est divisible par 2)

Le problème est que 13(base10)/3 n'est pas = à un nombre entier (car 13 est un nombre 1er)
Cherchons donc si parmi les nombre 113; 1113; 11113; 111113 etc. il en existe un pour lequel il est divisible par le produit de ses chiffres :

- 113(base10)/3 ~~ 37,667 (car 113 est un nombre 1er)
- 1113(base10)/3 = 371 !!!

Ainsi 1110, 1111, 1112, 1113 sont quatre entier consécutif prodigieux !

C'était si simple que je m'y suis perdu !
Encore merci !

Magyo