Angle entre deux vecteurs

[Chmiman]

Bonjour ,

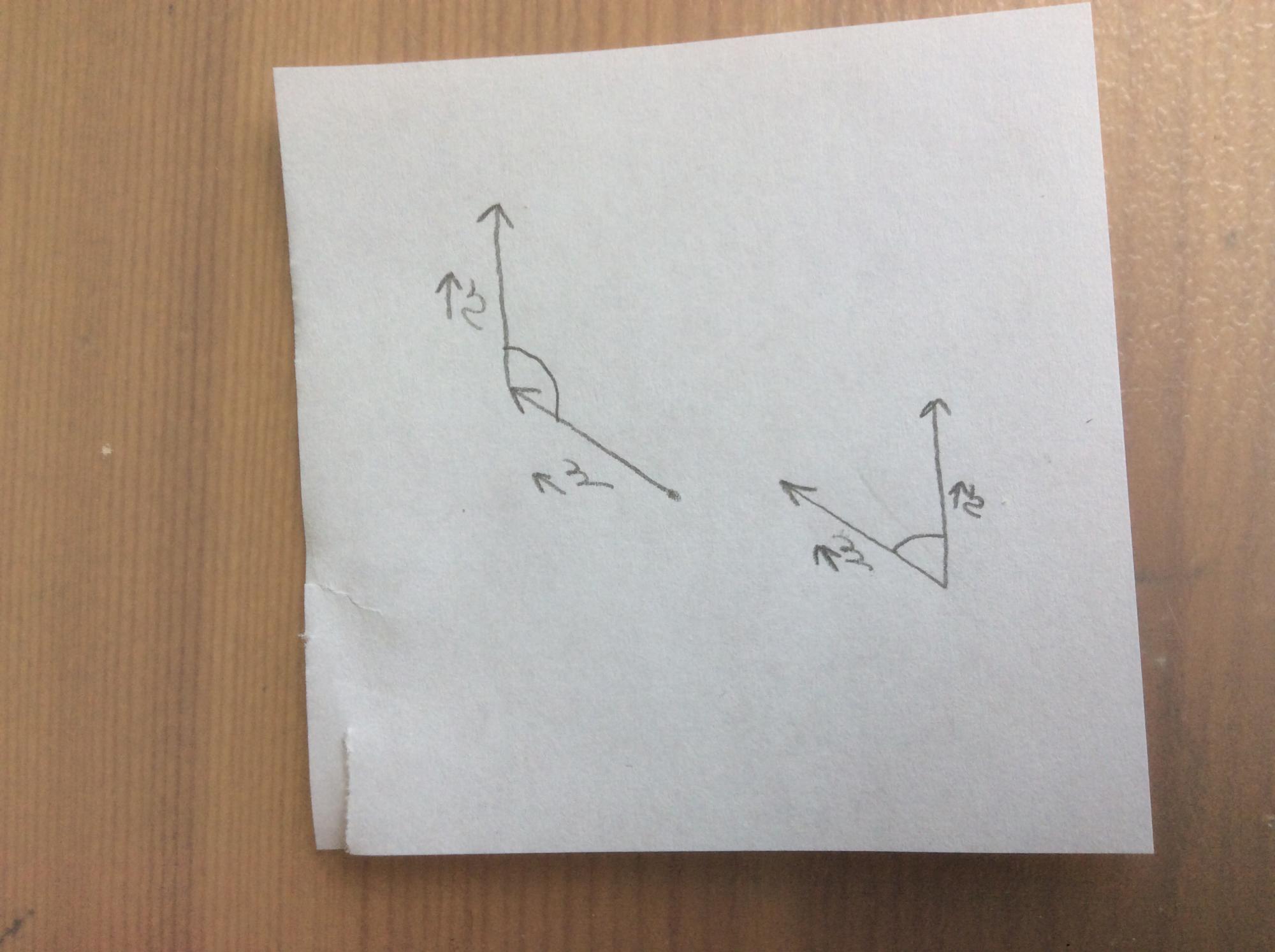
En trigo on voit les Angles orientés , avec des vecteurs , mais deux vecteurs on peut les placer où l'on veut , alors j'ai du mal à voir l'angle que deux vecteurs pourraient former si ils ne sont pas côte à côte mais si par exemple on les met bout à bout . Je pense qu'il me manque une notion peut être , mais deux objets que je peux bouger comment peuvent ils former un angle à tout moment ?

Ou alors il y a une def qui dirait que l'angle entre deux vecteurs se fait uniquement quand on met l'origine des deux sur un meme point , mais j'ai pas vu cette def alors je pose ma question !
-----

[Dynamix]

Salut

Décidément , tu ne digères toujours pas les vecteurs .
Tu ne vois les vecteur qu' à travers la notion géométrique , qui correspond en fait au bipoints .
L' angle entre deux bipoints , c' est l' angle entre les vecteurs colinéaire à ces bipoints .

On peut aussi passer par les vecteurs fixes , glissants , semi glissant , mais c' est moins rigoureux .

[ansset]

Bonjour ,

En trigo on voit les Angles orientés , avec des vecteurs , mais deux vecteurs on peut les placer où l'on veut ,
.......
alors je pose ma question !

tu donnes toi même la réponse et tu finis par la question.
à partir du moment ou tu as compris que tu peux les faire "glisser" comme tu veux ( pour reprendre l'expression de Dynamix )
Il te suffit de faire coïncider leurs deux origines.( sans changer leurs normes et directions )
par exemple au centre de ton plan.

[ansset]

ps : j'ai répondu à la forme de la question à savoir :
"alors j'ai du mal à voir l'angle que deux vecteurs pourraient former si ils ne sont pas côte à côte".
cela n'est bien entendu pas nécessaire pour des calculs éventuels par exemple sur les produits ( scalaire, vectoriel )

[A voir en vidéo sur Futura]

[Chmiman]

J'ai bien relu vos réponses , et j'ai beau chercher , deux vecteurs ne sont pas obligatoirement placés en coïncidant leurs origines , c'est ça que je comprends mal ! Imaginez deux vecteurs , que je place cette fois ci bout à bout , tel une relation de Chasles , ils forment un angle ces deux deux vecteurs , un angle différent que si on les avaient disposés différemment , par exemple en coïncidant leurs origines . Si vous me dites que c'est une convention et qu'il n'y a rien à comprendre sur pourquoi on coïncide leurs origines d'accord . Mais là c'est confus.

[ansset]

ps : je n'ai répondu qu'à la forme de la question à savoir :
"alors j'ai du mal à voir l'angle que deux vecteurs pourraient former si ils ne sont pas côte à côte".

rien à voir avec des calculs éventuels.

[Chmiman]

Tenez , pour illustrer #5 j'ai réalisé un dessin pour montrer les différents Angles que je peux faire en mettant les vecteurs comme je le souhaite ( j'ai le droit ).

[Dynamix]

deux vecteurs ne sont pas obligatoirement placés en coïncidant leurs origines

C' est vrai pour les bipoints pas pour les vecteurs .
Petit extrait de Wikipédia à cogiter :

La classe d'équivalence d'un bipoint (A, B) est appelée vecteur et est notée ***. Le bipoint (A, B) en est un représentant. Réciproquement, tout vecteur admet plusieurs bipoints représentants, dont aucun n'est privilégié. Si une origine est choisie, il existe un unique bipoint représentant un vecteur donné.

Si les vecteurs peuvent être déplacés dans le plan, quant à eux, les points ne le sont pas. Ces derniers restent fixes. L'intérêt d'avoir un représentant d'un vecteur est d'obtenir parmi les bipoints équipollents un seul dont l'origine ou l'extrémité est fixée une fois pour toutes.

https://fr.wikipedia.org/wiki/Vecteur#D.C3.A9finition

[Chmiman]

Avez vous vu ma photo ? Car j'ai fais une exemple concret du problème !

[Dynamix]

Avez vous vu ma photo ? Car j'ai fais une exemple concret du problème !

Le bon dessin , c' est celui ou les origines sont superposées .

[Chmiman]

D'accord mais ma question c'est justement pourquoi choisir un dessin plutôt qu'un autre ?

[Dynamix]

Réfléchis un peu ...
La figure de gauche montre l' angle entre -u et v

Comme je sens que tu vas demander pourquoi , je te réponds tout de suite : Par définition de l' angle entre deux vecteurs .

[jacknicklaus]

D'accord mais ma question c'est justement pourquoi choisir un dessin plutôt qu'un autre ?

Parce qu'il a bien fallu faire un choix, sinon on va ne sait plus de quoi on parle, d'un angle x ou de l'angle pi - x, ou de -x ou de x - pi. Pour faire des maths, il faut des définitions précises.

[Chmiman]

Merci de vos réponses . J'y penses j'ai une question qui porte sur le même thème et je trouve ça bête de recréer un post surtout que j'ai la reponse mais je sais pas comment l'expliquer , je m'explique : J'ai eu un exo avec deux vecteurs colinéaires de sens opposés , et il fallait que je calcule l'angle orienté , enfin que je détermine la mesure de cet angle plutôt ! Moi je me représente dans ma tete que l'angle ( u ; v ) peut être soit pi soit - pi , selon que j'ai tel ordre de vecteur ou tel ordre de sens de rotation ! Mais alors je choisi quoi , pi ou moins pi ? Sachant que je ne dois pas nécessairement mettre la mesure principale !

[Dynamix]

Tu mesures l' angle entre U et V en partant de U et en tournant dans le sens trigo .

[Chmiman]

Merci , donc pi !

[gg0]

Comme l'angle entre deux vecteurs est défini à 2pi près, prendre pi ou -pi ne change rien !

[Chmiman]

Sinon, il y a une raison mathématique qu'on aie choisi cette façon la de faire les Angles entre vecteurs ( pute curiosité mathématique ) ?

[gg0]

Les vecteurs ayant été définis assez rapidement à partir de bipoints avec origine et extrémités (donc illustrés par des flèches); il paraissait naturel de prendre deux bipoints de même origine pour définir l'angle, tout comme on prend deux demi droites de même origine pour définir des angles géométriques.
Donc pas de raison mathématique, simplement du bon sens.

[ENIMADADDEHC]

Bonjour ,
Vous avez effectuer une translation des vecteurs u et v donc il y a un changement dans l'orientation des angles trigonométrique .
il faut toujours penser a produit scalaire !
Chmiman