Recherche de tangente

[inviteda155e3d]

Bonjour à toutes et à tous,

Sur la figure faite avec matlab ci-dessous se trouve en bleue la courbe y = x + sin(x) et en jaune une courbe avec pour fonction y = kx (k étant la pente) que j'ai tracé un peu avec le pouce et j'aimerais faire cela plus rigoureusement. Le but étant de déterminer k pour que la courbe jaune soit tangente à la courbe bleue au point B sur le schéma. Ce point B étant localisé de manière à ce que la courbe bleue reste toujours au-dessus de la courbe jaune.

J'ai essayé de passer par le calcul de la dérivée mais je retombe toujours sur la courbe tracée en rouge, qui est bien tangente avec la bleue mais à l'origine ... Je dois passer à côté de quelque chose ...

Auriez-vous une suggestion ?

En vous remerciant par avance,

JB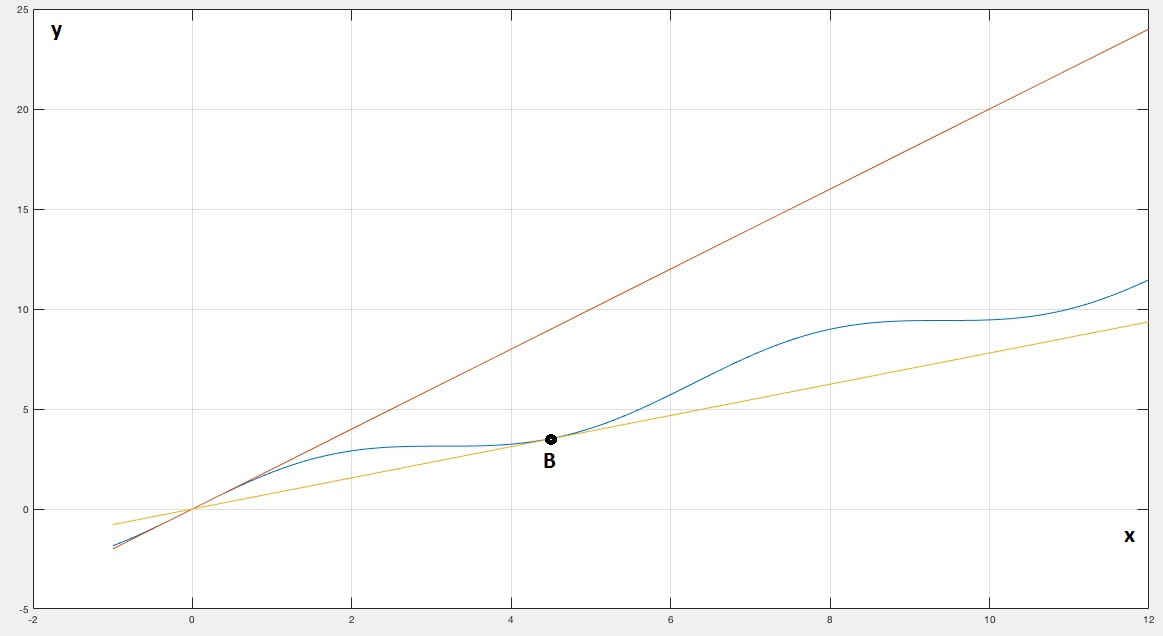
-----

[invited1ed38da]

Salut,

As-tu correctement utilisé la formule pour trouver l'équation d'une tangente en un point de la courbe d'une fonction dérivable en ce point?


Je te donne un petit indice qui devrait t'aider à localiser un B qui marche bien :
donc


Trace sur un graphe les courbes de f(x), de x-1 et de x+1, tu devrais avoir quelques intuitions à partir de là

[inviteda155e3d]

Salut,

Effectivement quand j'encadre sinx + x par x-1 et x+1, je trouve intuitivement que le point B se trouve à 3pi/2. Mais cet encadrement ne me convient pas car pour appliquer le "critère sectoriel" j'ai besoin que mes deux courbes encadrants sinx+x passes par l'origine (courbe rouge et bleue sur le graph dans mon premier message).

J'ai donc deux fonctions : y=sinx+x et y = kx, k étant une pente à déterminer. Pour ce faire j'ai essayé de passer par le calcul des tangentes au point B, disons (xb,yb). Cela me donne :
yb=(sinxb+xb)'(x-xb)+xb+sinxb
yb= (cosxb+1)(x-xb)+xb+sinxb
et
yb=(k*xb)'(x-xb)+kxb
yb=k(x-xb)+kxb

J'ai donc deux équations et trois inconnues (k, xb et yb)... Comment faire alors pour trouver les coordonnées (xb,yb) et la pente k? On s'entend c'est proche de x=3*pi/2 mais c'est pas exactement ça, un petit avant en faite ...

Merci,

[invited1ed38da]

Ah j'avais mal compris ce que tu voulais... Du coup ça me semble assez costaud!
J'ai quelque chose d'assez maladroit à te proposer mais après vérification graphique je crois que je suis sur le bon chemin, juste je n'arrive pas à trouver l'abscisse exacte de B.

Pour tout , la tangente à la courbe de au point d'abscisse a pour équation :

Toutes les tangentes ont une équation de cette forme. On cherche une de ces tangentes mais qui passerait par l'origine, c'est à dire dont l'ordonnée à l'origine serait nulle!





Donc on cherche un tel que soit un point fixe pour la fonction tangente, il est égal à son image par la fonction tangente.
On peut voir graphiquement que c'est vers a = 4.49.... et si tu traces la tangente à la courbe de sin(x) + x en ce point, tu t'aperçois que ça colle plutôt bien. Donc je pense que ma condition sur a est la bonne, après pour déterminer la valeur de ce point fixe je ne vois pas. Tu peux écrire un programme python très court qui te donnera une approximation (algorithme par dichotomie), mais pour la valeur exacte il va falloir que tu attendes plus fortiche que moi!

[A voir en vidéo sur Futura]

[gg0]

Bonjour.

Il est intuitif (mais pas si simple à prouver) que c'est la plus faible valeur solution strictement positive de tan(a)=a qui convient. Il n'y a pas de calcul avec des fonctions simples qui donne la valeur voulue, mais différentes méthodes permettent de trouver une approximation, par exemple Maple trouve a=4.493409458 environ. Matlab devrait te donner le même genre de résultat approché.

Cordialement.